形式语言笔记 - wuuconix's blog
形式语言笔记 - wuuconix's blog

第一章——绪论
语言是某个集合中的元素,按照规则组合乘的符号串的集合。
字母表
字母表是一个非空有穷集合,字母表中的元素称为该字母表的一个字母 letter。又叫做符号 symbol 或者字符 character
字符的两个特性
- 整体性 monolith 也叫做不可分性
- 可辨认性 distinguishable 也叫做可区分性。
字母表的乘积 Product
如果是字母表∑1\sum_1∑1和字母表∑2\sum_2∑2的乘积,则表示{ab ∣ a∈∑1, b∈∑2}\{ab\ |\ a\in \sum_1,\ b\in \sum_2\}{ab ∣ a∈∑1, b∈∑2}。
实际上就是字母表1中取个字符,字母表2中取1个字符,然后去连接。实际上就是笛卡尔积嘛
字母表的n次幂
∑0={ϵ}\sum^0=\{\epsilon\}∑0={ϵ}
这个埃普西隆表示是由字母表中0个字符组成的。
∑n=∑n−1∑\sum^n=\sum^{n-1}\sum∑n=∑n−1∑
符号表的正闭包和克林闭包
∑+=∑∪∑2∪∑3∪...\sum^{+}=\sum \cup \sum^2\cup\sum^3\cup...∑+=∑∪∑2∪∑3∪...
∑∗=∑0+∑+=∑0∪∑∪∑2∪∑3∪...\sum^{*}=\sum^0+\sum^+=\sum^0\cup\sum \cup \sum^2\cup\sum^3\cup...∑∗=∑0+∑+=∑0∪∑∪∑2∪∑3∪...
感觉在集合论中接触过类似的概念,好像在关系那块。
实际上正闭包就是从1次幂到n次幂的的并集
克林闭包比正闭包更多,比正闭包多了个0次幂,实际上就是多了个ϵ\epsilonϵ。
比如{0,1}+={0,1,00,01,10,11,000,001....}\{0,1\}^+=\{0,1,00,01,10,11,000,001....\}{0,1}+={0,1,00,01,10,11,000,001....}
{0,1}∗={ϵ,0,1,00,01,10,11,000,001....}\{0,1\}^*=\{\epsilon,0,1,00,01,10,11,000,001....\}{0,1}∗={ϵ,0,1,00,01,10,11,000,001....}
∑+\sum^+∑+ 中的元素是∑\sum∑中至少一个字符连接而成的字符串
∑∗\sum^*∑∗中的元素是∑\sum∑中的若干个,包括0个字符,连接而成的一个字符出啊
句子 sentence
若∑\sum∑是一个字母表,∀x∈∑∗\forall x\in \sum^*∀x∈∑∗,x叫做∑\sum∑上的一个句子。因为是从克林闭包中选择,所以一个句子可能是以恶孔子据
句子的长度 length
若x是一个句子,则x的长度实际就是其包含字符的个数,记作\abs{x}
长度为0的字符串叫做空句子,叫做ϵ\epsilonϵ。其长度\abs{\epsilon}=0
注意区分ϵ\epsilonϵ和ϕ\phiϕ的区分。
并置
实际上就是两个字符串的连接,并置又叫做连结。
串x的n次幂
之前讲了字母标的n次幂,是笛卡尔积。
串的x幂就很简单了,实际上就是n次连结。
x0=ϵx^0=\epsilonx0=ϵ
xn=xn−1xx^n=x^{n-1}xxn=xn−1x
比如x=110x=110x=110
则x4=110110110110x^4=110110110110x4=110110110110
前缀与后缀
设x,y,z,w,v∈∑∗x,y,z,w,v \in \sum^*x,y,z,w,v∈∑∗,且x=yzx=yzx=yz
- y是x的前缀 prefix
- 如果z≠ϵz \ne \epsilonz=ϵ 则y是x的真前缀 proper prefix
- z是x的后缀 suffix
- 如果y不是空句子,则z是x的真后缀 proper suffix
公共前缀与后缀
- 如果x=yz, w=yv ,则y是x和w的公共前缀 common prefix
- 如果x和w的任何公共前缀都是y的前缀,则y是x和w的最大公共前缀。
- 如果x=zy, w=vy,则y是x和w的公共后缀 common suffix
- 如果x和w的任何公共后缀都是y的后缀,则y是x和w的最大公共后缀。
子串 substring
w,x,y,z∈∑∗w, x, y, z \in \sum^*w,x,y,z∈∑∗,且w=xyz,则称y是w的字串
公共子串
t,u,v,w,x,y,z∈∑∗t, u, v, w, x, y, z \in \sum^*t,u,v,w,x,y,z∈∑∗,且t=uyv,w=xyzt=uyv, w=xyzt=uyv,w=xyz,则称y是t和w的公共子串 common substring 如果在众多子串中你是最长的,则你被称为t和w的最大公共子串
两个串的最大公共子串不一定是唯一的。
比如acccxdddb 和mcccydddn 的最大子串为 ccc 和ddd,它们的长度都为3。1
语言 language
∀L⊆∑∗\forall L\subseteq \sum^*∀L⊆∑∗,称L为字母表∑\sum∑上的一个语言 language
∀x∈L\forall x\in L∀x∈L,称x为L上的一个句子。
实际上给定一个字母表,就比如英语的a到z,包括一些其他的标点符号 它的克林闭包里面的元素实际上是无限的,然后我们在这些无数的元素中选出一些便作为了一个语言。
所以语言实际上就是一个集合。
集合里面的每一个元素都是一个句子。
语言的乘积 product
L1⊆∑1∗,L2⊆∑2∗L_1 \subseteq \sum_1^*, L_2 \subseteq\sum_2^*L1⊆∑1∗,L2⊆∑2∗,语言L1L_1L1和L2L_2L2的乘积是一个语言,该语言的定义为L1L2=xy∣x∈L1,y∈L2L_1L_2={xy|x\in L_1,y\in L_2}L1L2=xy∣x∈L1,y∈L2是字母表∑1∪∑2\sum_1 \cup \sum_2∑1∪∑2上的语言。
对于语言,也有幂的概念。当了有了幂的概念,就也能定义正闭包和克林闭包啦!
我们之前接触幂实际上是从字母表的幂开始,然后从字母表的幂定义字母表的克林闭包。然后从克林闭包中选择一些元素作为语言。 实际上幂的概念是定义在集合上的。字母表是一个字符的集合,语言是一些句子的集合。它们本质上是一样的。 所以幂、闭包这些概念都是相同的。

第二章——文法
文法
G=(V, T, P, S)
V 为变量 variable 的非空有穷集。∀A∈V\forall A \in V∀A∈V,A叫做一个语法变量 syntactic Variable ,简称为变量,也可叫做非终极符号 nonterminal。
T 为中级符 terminal 的非空有穷集 ∀a∈T\forall a\in T∀a∈T,a叫做终极符。V∩T=ϕV \cap T = \phiV∩T=ϕ
P为产生式 production 的非空有穷集合。P中的元素均具有α→β\alpha \rightarrow \betaα→β,被称为产生式。读作α定义为β。其中α∈(V∪T)+\alpha \in (V \cup T)^+α∈(V∪T)+,且α\alphaα中至少有V中元素的一个出现。β∈(V∪T)∗\beta\in(V\cup T)^*β∈(V∪T)∗
S为文法G的开始符号 start symbol
关于产生式,如果有某个变量可以定义多个元素,可以进行缩写。被定义的那些被称为候选式 candidate

推导 derivation
α→β\alpha \rightarrow \betaα→β 这是a定义b。
推导则是rightArrow

根据α能够定义β。则γαβ⇒Gγβδ\gamma\alpha\beta\Rightarrow_G \gamma\beta\deltaγαβ⇒Gγβδ 读作前者能够在文法G中直接推导除后者。
规约 reduction
感觉就是推导的逆?前者能够推导出后者。后者能够规约为前者。

然后推导的那个G下标可以省略不写。
直接写为⇒\Rightarrow⇒
⇒n\Rightarrow^n⇒nb表示前者在G中经过n步推导式后者,也可以说后者经过n步规约为前者。
⇒+\Rightarrow^+⇒+表示前者在G中经过至少1步推导除后者,后者经过至少1步规约为前者。
⇒∗\Rightarrow^*⇒∗表前者在G中经过若干步(包括0步)推导后者,后者在G中经过若干步规约为前者。
如果⇒0\Rightarrow^0⇒0是什么情况呢?实际上就是前者等于后者了,因为前者不用推导就得到了后者,后者不用规约就得到了前者。
然后普通得⇒\Rightarrow⇒不写任何东西的话,实际上省略了“1”,因为前者需要一次推导为后者,后者需要1次规约规约为前者。
文法下的 语言 句子 句型的定义

这里语言被定义为了,首先是终结符表集合的克林闭包中的一个值,并且可由开始符号推出。
句子还是一样的定义,是语言的一个元素
这里还有句型的概念,句型和句子有什么区别呢?我们可以看到句型是在(V∪T)∗(V \cup T)^*(V∪T)∗中的一个元素,也就是说句型是可以包含变量的,而句子则没有变量,只有终结符。
但是并不说所有的句型里都有变量,没有变量也是可以的。

这样想来,是不是可以说所有的句子是句型呢?
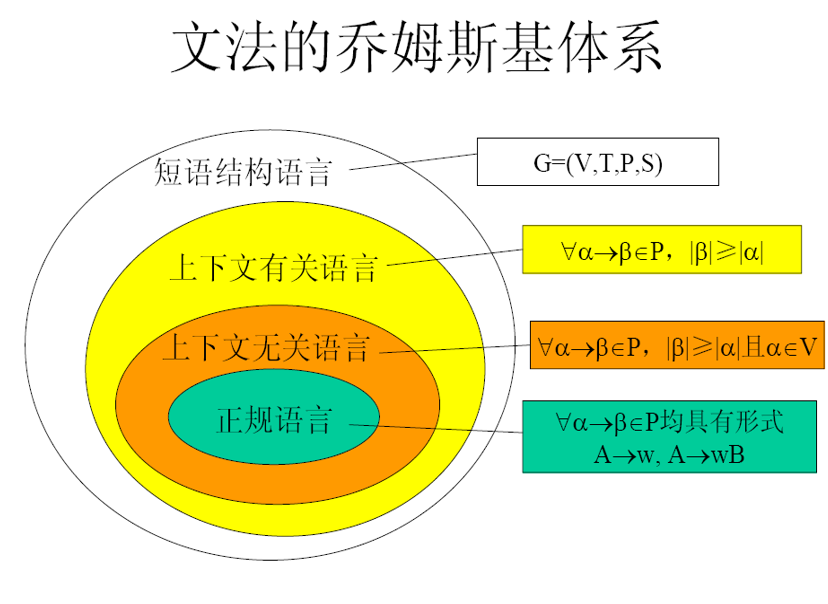
0型文法
ppt上没有讲怎么样的文法叫0型文法 type 0 grammar ,也叫做短语结构文法 phrase structure grammar PSG
0型文法产生的语言叫做0型语言 phrase structure language,也可以叫做短语结构语言
0型文法是最最基础的文法。它没有任何限制条件,所以可以这样说,所有的文法都属于0型文法。
1型文法
如果G是0型文法。然后对于 ∀α→β∈P\forall\alpha\rightarrow\beta\in P∀α→β∈P,均有\abs{\beta}\geq\abs{\alpha}成立。则G为1型文法或者上下文有关文法。 context sensitive grammar CSG
有G产生出的语言叫做1型语言或者上下文有关语言 CSL
1型文法实际上就是规定了产生式的右侧长度必须大于左侧长度。
2型文法
若G是1型文法。若对于∀α→β∈P\forall\alpha\rightarrow\beta\in P∀α→β∈P,均有\abs{\beta}\geq\abs{\alpha}成立,并且α∈V\alpha \in Vα∈V成立(V是语法变量的集合),则称G为2型文法 或者上下文无关文法 context free grammar CFG
由G产生的语言叫做2型语言 或者上下文无关语言 context free language CFL。
实际上2型文法就是1型文法的基础上加上了产生式左侧的必须是一个语法变量,注意是一个,不能多,只有单个语法变量。
3型文法
G是2型文法。如果对于∀α→β∈P\forall\alpha\rightarrow\beta\in P∀α→β∈P,α→β\alpha\rightarrow\betaα→β均具有形式 A→wA\rightarrow wA→w,A→wBA\rightarrow wBA→wB。其中A,B∈V w∈T+A,B\in V\ \ w\in T^+A,B∈V w∈T+。则称G为3型文法,也可称为正则文法 regular grammar RG 或者正规文法。 由G产生的语言叫做3型语言,可以称为正则语言或者正规语言 regular language RL。
之前2型文法规定了产生式左侧必须是单个语法变量,而没有规定产生式右侧到底是什么。
而3型文法就去规定了产生式右侧。3型文法规定产生式右侧可以有语法变量(最好的情况就是没有了,只有终结符号),如果有语法变量,那么这个语法变量只能有一个,并且放在最右侧。它前面都是终结符号。
定理2-1
L是RL的充要条件是存在一个文法,该文法产生语言L,并且它的产生式要么是形如A→aA\rightarrow aA→a的产生式,要么是形如A→aBA\rightarrow aBA→aB的产生式。其中A,BA,BA,B为语法变量,a为终极符号。
不证自明。这里的产生式就是正则文法。一个正则文法产生的语言一定是正则语言。 而一个正则语言也一定是一个正则文法产生的。
线性文法
设G=(V, T, P, S),如果对于∀α→β∈P\forall\alpha\rightarrow\beta\in P∀α→β∈P, α→β\alpha\rightarrow\betaα→β 均具有如下形式:
A→wA\rightarrow wA→w
A→wBxA\rightarrow wBxA→wBx
其中A,B∈V,w,x∈T∗A, B\in V, w,x \in T^*A,B∈V,w,x∈T∗,则称G为线性文法。 liner grammar
线性文法产生的语言叫做线性语言。
右线性文法
设G=(V, T, P, S),如果对于∀α→β∈P\forall\alpha\rightarrow\beta\in P∀α→β∈P, α→β\alpha\rightarrow\betaα→β 均具有如下形式:
A→wA\rightarrow wA→w
A→wBA\rightarrow wBA→wB
其中A,B∈V,w∈T∗A, B \in V, w\in T^*A,B∈V,w∈T∗,则称G为右线性文法 right liner grammar
右线性文法长生的语言叫做右线性语言。
左线性文法
设G=(V, T, P, S),如果对于∀α→β∈P\forall\alpha\rightarrow\beta\in P∀α→β∈P, α→β\alpha\rightarrow\betaα→β 均具有如下形式:
A→wA\rightarrow wA→w
A→BwA\rightarrow BwA→Bw
其中A,B∈V,w∈T∗A, B \in V, w\in T^*A,B∈V,w∈T∗,则称G为左线性文法 left liner grammar
左线性文法长生的语言叫做左线性语言。
定理2-2
和定理2-1类似。L是一个左线性语言的充要条件是 存在文法G,G中的产生式是形如 A→aA\rightarrow aA→a 或者A→BaA\rightarrow BaA→Ba,使得L(G)=LL(G)=LL(G)=L。
定理2-3
左线性文法和右线性文法等价。
定理2-4
左线性文法的产生式和右线性文法的产生式混用所得到的文法不是RG。
空语句
形如A→ϵA\rightarrow\epsilonA→ϵ的产生式叫做空产生式,也可叫做ϵ\epsilonϵ产生式。
我们可以回想一下1型文法的概念,它产生式右侧的长度需要大于等于右侧的长度。所以空语句是不符合1型文法的,因为空语句的右侧是ϵ\epsilonϵ,它的长度是0。
所以空语句不能出现在1型文法,2型文法,正则文法中,也就不能出现在1型语言、2型语言、正则语言中。
但是为了方便研究某些问题。我们将手动将S→ϵS\rightarrow \epsilonS→ϵ加入到产生式中,并且规定这样不会影响到文法的类型。

同样的,加入空语句也不会影响语言的类型。去掉也不会233。

、

第三章——有穷状态自动机
定义
M=(Q,∑,δ,q0,F)M=(Q, \sum, \delta,q_0,F)M=(Q,∑,δ,q0,F)。 finite automanton FA
Q表示状态的非空有穷集合。 ∀(q)∈Q\forall(q)\in Q∀(q)∈Q,q称为M的一个状态 state。
∑\sum∑表示输入字母表 input alphabet。输入字符串都是∑\sum∑上的字符串。
用∑\sum∑来表示字母表实际上从第一章就开始了
q0q_0q0 q0∈Qq_0\in Qq0∈Q,是M的开始状态 initial state。也可叫做初始状态或者启动状态。
δ\deltaδ 状态转移函数 transition function。有时候又叫做状态转移函数函数或者移动函数。

F F⊆QF\subseteq QF⊆Q 是M的终止状态 final state集合。 ∀q∈F\forall q\in F∀q∈F,称q为M的终止状态,又称为接受状态 accept state。
FA的两种表示法
状态转移表和状态转换图。

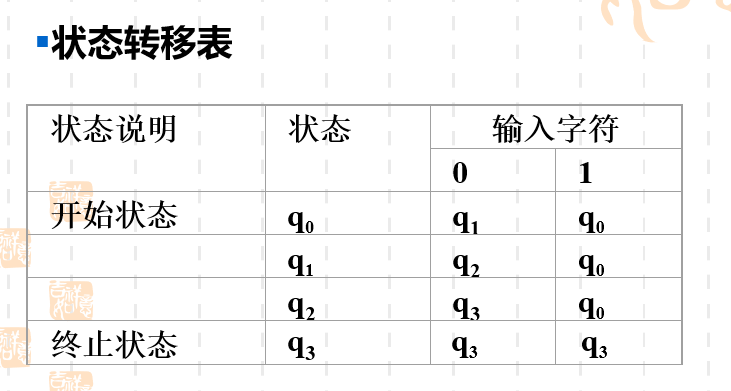
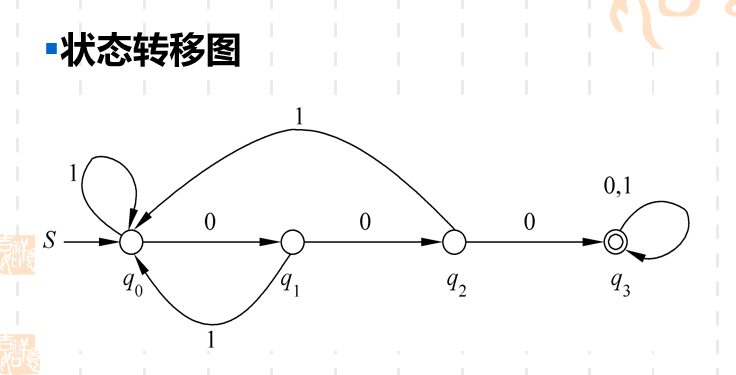
状态转移表实际上就是把所有的状态列出来,然后把它们输入不同字符下对应的结果都写下来。然后在开始状态和终止状态前面进行一个标识。
状态转移图中每个状态都是一个顶点。转化的过程用一个弧来标识,弧上面标识的内容标识输入的字符。终止状态用双层圈标出。开始状态用一个S指向,表示start之意。
对δ\deltaδ的扩充
之前将的状态转移函数,都是一个接收一个输入字符然后转移到另一个状态。如果想要一次性接收多个字符,然后直接得到状态结果呢?
这就是δ^\hat{\delta}δ^。
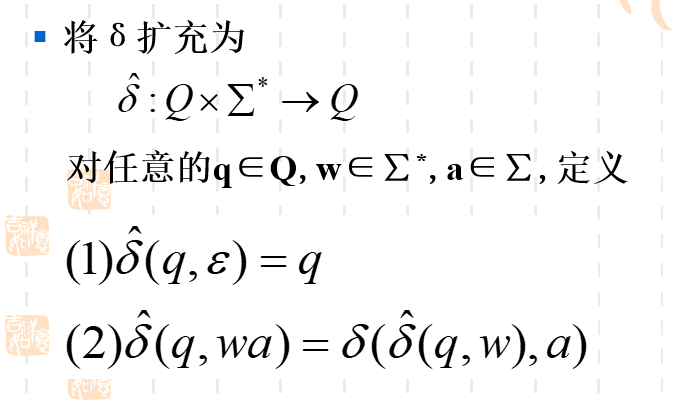

实际上两者没有任何区别,只是迭代的关系。如果我们一次性接收了多个字符,那就用迭代的方式一个个来处理,从左往右,进行状态的转化。
所以我们可以将δ^\hat{\delta}δ^简记为δ\deltaδ
确定的有穷状态自动机 DFA
对于任意的q∈Qq\in Qq∈Q,a∈∑a\in\suma∈∑,δ(q,a)\delta(q,a)δ(q,a)均有确定的值,所以将这种FA称为确定的有穷状态自动机 deterministic finite automanton DFA。

一些结论
- 一般来说定义FA时,不用具体写出M=(Q,∑,δ,q0,F)M=(Q,\sum,\delta,q_0,F)M=(Q,∑,δ,q0,F)这种复杂的东西。 只需要给出一个直观的状态转移图即可。从状态转移图上我们可以清楚的看到状态们,输入字符们,转移们,开始状态和接收状态们。
- 对于DFA来说,每个顶点的出度恰好就是输入字母表中所含的字符个数。 因为DFA是确定的有穷状态自动机,它的每个状态对于任何的输入字符都又一个确定的状态。故它一定会有输入字母表中所含字母个数条边。
- 字符x被FA M所接受的充要条件是 在M的状态转移图中存在 一条从开始状态到某一终止状态的有向路,该有向路上从第一条边到最后一条边的标记依次并置而构成字符串x。
- 一个FA有且只有一个初始状态,但是可能有多个终止状态。 比如一下这个FA就有两个终止状态。
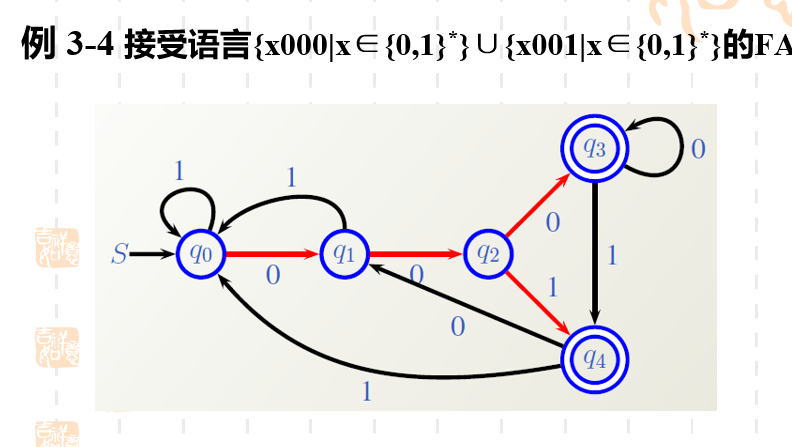
即时描述 instantaneous description, ID。
x,y∈∑∗,δ(q0,x)=qx,y \in \sum^*,\delta(q_0,x)=qx,y∈∑∗,δ(q0,x)=q,xqy称为M的一个即时描述。表示xy是M正在处理的一个字符串,x引导M从q0q_0q0(即开始状态)启动并到达状态q,M但概念正注释着y的首字符。
如果xqay是M的一个即时描述,且δ(q,a)=p\delta(q,a)=pδ(q,a)=p
则xqay├M xapyxqay ├_M\ xapyxqay├M xapy


这和之前规约⇒\Rightarrow⇒省略G一样,这里可以省略M。
FA和DFA的区别
- FA并不是对于所有的(q,a)∈Q×∑, δ(q,a)(q,a)\in Q\times\sum,\ \delta(q,a)(q,a)∈Q×∑, δ(q,a)都有状态与它对应。 也就是它的出度可以小于输入表字符的个数
- FA并不是对于所有的(q,a)∈Q×∑,δ(q,a)(q,a)\in Q\times\sum, \delta(q,a)(q,a)∈Q×∑,δ(q,a) 只对应一个状态 第一条性质还好理解。这条就更牛逼了,也就是说输入一个字符,进行状态转移的时候可能会进入两个状态中去,非常神奇。
- FA在任意时刻可以处于有穷多个状态
- FA具有智能
NFA的形式定义
不确定的有穷状态自动机 non-deterministic finite automanton NFA
M是一个五元组 M=(Q,∑,δ,q0,F)M=(Q, \sum, \delta,q_0,F)M=(Q,∑,δ,q0,F)
我们发现NFA的式子和之前的FA的式子完全一致。这也非常好理解,因为NFA和DFA一样,都是FA。
只不过它的状态转移函数和DFA不同。
δ:Q×∑→2Q\delta: Q\times\sum\rightarrow 2^Qδ:Q×∑→2Q,对于∀(q,a)∈Q×∑, δ(q,a)={p1,p2,...pm}\forall(q,a)\in Q\times\sum,\ \delta(q,a)=\{p_1,p_2,...p_m\}∀(q,a)∈Q×∑, δ(q,a)={p1,p2,...pm}表示M在状态q读入字符a,可以选择地将状态变为p1p_1p1或者p2p_2p2,…或者pmp_mpm,并将读头向右移动一个带方格而指向输入字符串的下一个字符。
FA的状态转移图、FA的状态对应的等价类、FA的即时描述对NFA都有效。
很显然,不然就不叫"FA"的状态转移图了。 之前我们学的都是FA下的一些定义,只不过FA用的例子都是DFA的。
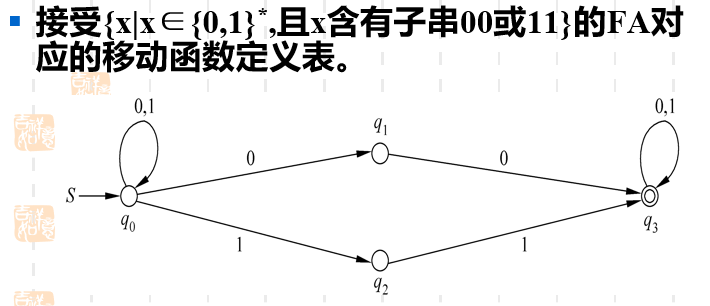
我们可以从这个例子中看到,q0q_0q0状态在接受到0这个输入字符串的时候,它会进行选择,可能转移到q0q_0q0状态,也可能转移到q1q_1q1状态。再看q1q_1q1状态,只有一个出度,也就是它只会去接受输入字符串中的"0",而直接忽略掉"1"。
同样,如果一次性输入多个字符,就需要对δ\deltaδ进行扩充。



第一次对δ\deltaδ的扩充相当于能够让状态转移函数一次性能够接受多个输入字符,然后进行状态转移。
而第二次扩充相当于是让一开始的初始状态变成多个。相当于现在可以多个初始状态 同时接受到多个输入字符,然后进行状态转化。
NFA M接受(识别)的语言
- 对于∀(x)∈∑∗\forall(x)\in\sum^*∀(x)∈∑∗,如果δ(q0,x)∩F≠ϕ\delta(q_0,x) \cap F\ne\phiδ(q0,x)∩F=ϕ 则称x被M接受,如果δ(q0,x)∩F=ϕ\delta(q_0,x) \cap F = \phiδ(q0,x)∩F=ϕ 则称M不接受x。
- L(M)={x∣x∈∑∗且δ(q0,x)∩F≠ϕ}L(M)=\{x|x\in \sum^* 且 \delta(q_0,x) \cap F \ne \phi \}L(M)={x∣x∈∑∗且δ(q0,x)∩F=ϕ} 称为M接受(识别)的语言。
NFA和DFA等价
- 对于一个输入字符,NFA可以进入若干个状态,而DFA智能进入一个唯一的状态
- 虽然从DFA看待的角度来说,NFA在某个时刻同时进入了若干个状态,但是,这若干个状态合起来的总效果相当于它处于这些状态对应的一个综合状态。因此我们考虑让DFA用一个状态来对应NFA的一组状态。

NFA转化为DFA的例子
上面讲了NFA与DFA的对应关系。这里给出一个实际转化的实例。
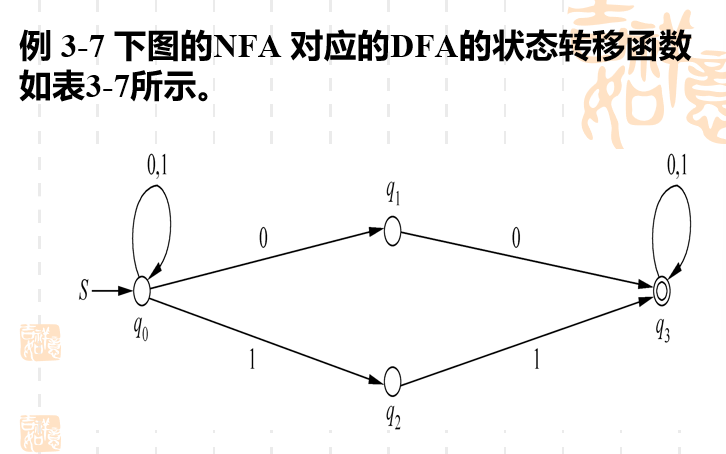
这里的[q0,q1][q_0,q_1][q0,q1]是什么意思呢?在NFA看来q0q_0q0是一个状态,q1q_1q1也是一个状态,而对于NFA来说,在初始状态为q0q_0q0的情况下 ,接受输入字符为0,那么它既可以到q0q_0q0,也可以到q1q_1q1。
但是DFA是不能实现这一点的,所以我们就把到达q0q_0q0或者到达q1q_1q1想象成一个状态,一个综合状态,这就是[q0,q1][q_0,q_1][q0,q1]的含义了。
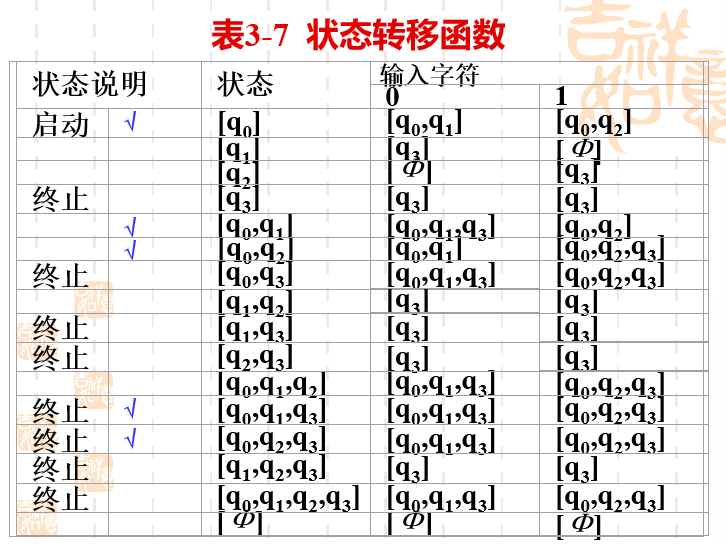
这个状态转移图就是把所有可能的综合状态遍历的一遍,首先是单个状态的综合状态 [q0]、[q1]、..[q3][q_0]、[q_1]、..[q_3][q0]、[q1]、..[q3],到最后4个状态的的综合状态[q0,q1,q2,q3][q_0,q_1,q_2,q_3][q0,q1,q2,q3]。分别写出它们在获得输入字符后的状态转移。
这里举个例子,我们要获得[q0,q1,q2,q3][q_0,q_1,q_2,q_3][q0,q1,q2,q3]在输入字符为0的情况下的转移状态要怎么办呢?我们就看这个综合状态中的每个状态获得字符0的情况,q0q_0q0获得0会到q0q_0q0和q1q_1q1。q1q_1q1获得0会到q3q_3q3,q2q_2q2不会获得0, q3q_3q3获得0会到q3q_3q3。所以综合一下可能的状态是q0,q1,q3q_0,q_1,q_3q0,q1,q3,同样由于DFA无法同时处理三个状态,便把它们假象称为一个综合状态[q0,q1,q3][q_0,q_1,q_3][q0,q1,q3]。这和表中的结果也是一致的。
同时我们注意到表格中有些打了勾,有些没打,那是什么意思呢?这里需要引出不可达状态的概念。
不可达状态(inaccessible state):不存在从[q0][q_0][q0]对应的顶点出发,到达该状态对应的顶点的路。我们称此状态 从开始状态是不可达的。
我们看[q0][q_0][q0]会到达[q0,q1][q_0,q_1][q0,q1]和[q0,q2][q_0,q_2][q0,q2]。然后[q0,q1][q_0,q_1][q0,q1]会到达[q0,q1,q3][q_0,q_1,q_3][q0,q1,q3]和[q0,q2][q_0,q_2][q0,q2]。[q0,q2][q_0,q_2][q0,q2]会到达[q0,q1][q_0,q_1][q0,q1]和[q0,q2,q3][q_0,q_2,q_3][q0,q2,q3]。
之后再看[q0,q1,q3][q_0,q_1,q_3][q0,q1,q3]会到达[q0,q1,q3][q_0,q_1,q_3][q0,q1,q3]和[q0,q2,q3][q_0,q_2,q_3][q0,q2,q3]。q[q0,q2,q3]q[q_0,q_2,q_3]q[q0,q2,q3]会到达[q0,q1,q3][q_0,q_1,q_3][q0,q1,q3]和[q0,q2,q3][q_0,q_2,q_3][q0,q2,q3]。 没有再产生新的状态。之前提到的所有综合状态都是可达的。没有提到的就是不可达的。也被称为无用的。
然后我们一开始写表格的时候不用把所有的综合状态都写出来,因为肯定有很多状态是无用的。我们完全可以从[q0][q_0][q0]开始,只写可达的综合状态。


这样就可以不用再把所有的综合状态都写出来了,节约了时间。
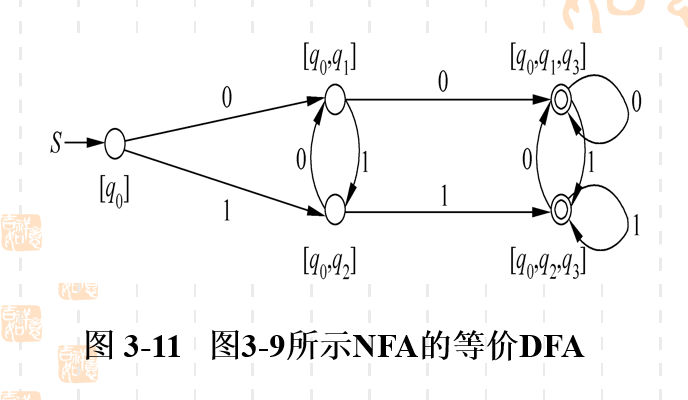
以下为最终DFA状态转换图。
带空移动的有穷状态自动机
non-deterministic finite automanton with ϵ−moves\epsilon-movesϵ−moves ϵ−NFA\epsilon-NFAϵ−NFA
我们之前的FA的输入字符都至少有1个,当时嫌太少还将状态转移函数拓展为了一次性可以接收多个输入字符。但要是这个输入字符为空串呢?
如果我们允许NFA的输入字符为空串,那么就是ϵ−NFA\epsilon-NFAϵ−NFA了。


我们可以看到ϵ−NFA\epsilon -NFAϵ−NFA看起来很吊,但实际上这里的δ\deltaδ只能接收一个字符或者空串,不能同时接收多个字符。这里同样需要像之前的DFA和NFA一样对δ\deltaδ进行拓展。

以下是一些晦涩的概念。
- ϵ−clousure(q)={p∣从q到p有一条标记为ϵ的路}\epsilon-clousure(q)=\{p|从q到p有一条标记为\epsilon的路\}ϵ−clousure(q)={p∣从q到p有一条标记为ϵ的路} clousure是闭包的意思,这里的"-“也不是减法的意思,类似于密码学中的"M-序列”,只是一个连接符。 所以ϵ−closure(q)\epsilon-closure(q)ϵ−closure(q)就是q可以不读入任何值直接进行状态转化到的状态的集合。
- ϵ−closure(P)=∪p∈Pϵ−clousure(p)\epsilon-closure(P)=\cup_{p\in P} \epsilon-clousure(p)ϵ−closure(P)=∪p∈Pϵ−clousure(p) 上一条是单个状态的埃普西隆闭包。 这里扩充为了一个集合的埃普西隆闭包。实际上就是这个集合中所有状态的闭包之和,但是为了去重利用了并集运算。
- δ^(q,ϵ)=ϵ−closure(q)\hat{\delta}(q,\epsilon)=\epsilon-closure(q)δ^(q,ϵ)=ϵ−closure(q)
- δ^(q,wa)=ϵ−closure(P)\hat{\delta}(q,wa)=\epsilon-closure(P)δ^(q,wa)=ϵ−closure(P) P={p∣∃r∈δ^(q,w)P=\{p|\exists r\in \hat{\delta}(q,w)P={p∣∃r∈δ^(q,w) 使得p∈δ(r,a)}p\in\delta(r,a)\}p∈δ(r,a)} = ∪r∈δ^(q,w)δ(r,a)\cup_{r\in\hat{\delta}(q,w)}\delta(r,a)∪r∈δ^(q,w)δ(r,a)
对于任意的(P, a)∈2Q×∑\in 2^Q \times \sum∈2Q×∑
- δ(P,a)=∪q∈Pδ(q,a)\delta(P,a)=\cup_{q\in P}\delta(q,a)δ(P,a)=∪q∈Pδ(q,a) 这实际上非常好理解,P是一些状态的集合,这些状态们接收到了a进行状态转化,然后就是每个状态转化后转台的集合,因为一些状态可能会转化到同一个状态,所以用并集去重
- δ^(P,w)=∪q∈qδ^(q,w)\hat{\delta }(P,w)=\cup_{q\in q}\hat{\delta}(q,w)δ^(P,w)=∪q∈qδ^(q,w)
看到这么多概念你可能已经晕了,我们用下面这个例子来把以上的概念运用起来。
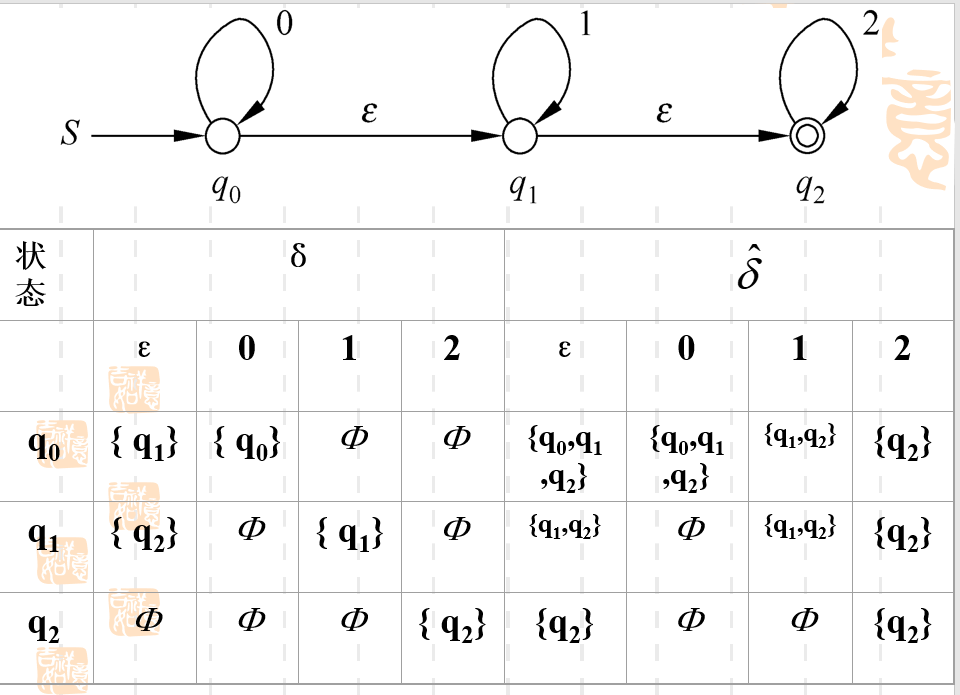
普通的δ\deltaδ不必多说,直接看图就ok,比如q1q_1q1遇到输入ϵ\epsilonϵ时就会转化为q2q_2q2。
关键是δ^\hat{\delta}δ^。
δ^(q0,ϵ)\hat{\delta}(q_0,\epsilon)δ^(q0,ϵ)要怎么求呢?
实际上这就是上面的定义3 δ^(q,ϵ)=ϵ−closure(q)\hat{\delta}(q,\epsilon)=\epsilon-closure(q)δ^(q,ϵ)=ϵ−closure(q)
故δ^(q0,ϵ)=ϵ−closure(q0)\hat{\delta}(q_0,\epsilon)=\epsilon-closure(q_0)δ^(q0,ϵ)=ϵ−closure(q0) 。
然后这个埃普西隆闭包怎么求呢,它的定义为那些和开始符号之间有ϵ\epsilonϵ路的状态的集合。
实际上,之前定义里没有说清楚,ϵ−closure(q)\epsilon-closure(q)ϵ−closure(q)时包含自己q本身的,因为可以想为自己通过输入的空串转移为了自己,因为这个过程就像什么都没有动一样,所以图里一般应该也不会标。
然后q1q_1q1很显然在这个空串闭包中,图中都标了,然后这个q2q_2q2应该也算,因为q0q_0q0到q2q_2q2看起来貌似要经过2ϵ2\epsilon2ϵ的一条路,但是实际上由于ϵ\epsilonϵ时一个空串,两个空串和一个空串一样,都是空串,可以和0=2×00=2\times00=2×0做类比。
所以ϵ−closure(q0)={q0,q1,q2}\epsilon-closure(q_0)=\{q_0,q_1,q_2\}ϵ−closure(q0)={q0,q1,q2}
然后我们再看δ^(q0,0)\hat{\delta}(q_0,0)δ^(q0,0)是怎么求的,我们需要利用上面的定义4。
δ^(q,wa)=ϵ−closure(P)\hat{\delta}(q,wa)=\epsilon-closure(P)δ^(q,wa)=ϵ−closure(P)
P={p∣∃r∈δ^(q,w)P=\{p|\exists r\in \hat{\delta}(q,w)P={p∣∃r∈δ^(q,w) 使得p∈δ(r,a)}p\in\delta(r,a)\}p∈δ(r,a)}
= ∪r∈δ^(q,w)δ(r,a)\cup_{r\in\hat{\delta}(q,w)}\delta(r,a)∪r∈δ^(q,w)δ(r,a)
这里把δ^(q0,0)\hat{\delta}(q_0,0)δ^(q0,0)看作δ^(q0,ϵ0)\hat{\delta}(q_0,\epsilon0)δ^(q0,ϵ0)
有δ^(q0,ϵ0)=ϵ−closure(P)\hat{\delta}(q_0,\epsilon0)=\epsilon-closure(P)δ^(q0,ϵ0)=ϵ−closure(P)
P={p∣∃r∈δ^(q0,ϵ)P=\{p|\exists r\in \hat{\delta}(q_0,\epsilon)P={p∣∃r∈δ^(q0,ϵ) 使得p∈δ(r,0)}p\in\delta(r,0)\}p∈δ(r,0)}
= ∪r∈δ^(q0,ϵ)δ(r,0)\cup_{r\in\hat{\delta}(q_0,\epsilon)}\delta(r,0)∪r∈δ^(q0,ϵ)δ(r,0)
实际上是怎么样呢?首先我们先求一个叫做P的状态集合。
里面记录的状态都是什么呢?
是q0q_0q0的空串闭包里的状态在输入0转移后的状态们。
之前求了,q0q_0q0的空串闭包里有{q0,q1,q2}\{q_0,q_1,q_2\}{q0,q1,q2}。它们输入零后,只剩下了q0q_0q0。所以P就是{p0}\{p_0\}{p0}
然后我们再求这个P的空串闭包就可以啦,p0p_0p0的空串闭包是{q0,q1,q2}\{q_0,q_1,q_2\}{q0,q1,q2}。
所以δ^(q0,0)\hat{\delta}(q_0,0)δ^(q0,0)就是{q0,q1,q2}\{q_0,q_1,q_2\}{q0,q1,q2}啦!
我们再做一个δ^(q0,2)\hat{\delta}(q_0,2)δ^(q0,2)。
先求P,就是p0p_0p0的空串闭包在输入2后的转移状态们,发现只有q2q_2q2。
然后就是q2q_2q2的空串闭包,很显然q2q_2q2后继无人了,它的空串闭包只有自己了。
故δ^(q0,2)={q2}\hat{\delta}(q_0,2)=\{q_2\}δ^(q0,2)={q2}。
虽然空串闭包中可能只有一个元素,但是仍然要写成一个集合的形式,因为空串闭包定义的时候就是定义的一个集合。而且这个集合不会是一个空集合,因为任何状态的空串闭包中肯定有自己。
通过以上的例子,我们已经知道了ϵ−NFA\epsilon-NFAϵ−NFA中δ^\hat{\delta}δ^的求法。也能够发现,由于定义的不一样,盖帽转移和转移是完全不一样的结果【从结果中很容易看出来,想象一下求得过程也很容易理解】
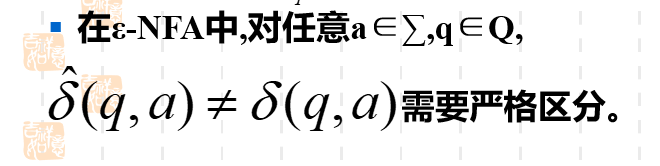
我们在已经了解δ^\hat{\delta}δ^在理论上得求法之后,我们再重新审视一下δ\deltaδ盖帽到底求的是什么,能不能通过我们朴素的直觉看到它的结果。

ϵ−NFA\epsilon-NFAϵ−NFA接受的语言

定理3-2
空串NFA和NFA是等价的。

构造起来非常简单,状态转移函数直接不用该,直接搬过去。
然后对应NFA的终结符号集合可能需要改变。
如果原本的终结符号集合和开始符号的空船闭包有交集,那么q0q_0q0也需要加入到对应NFA的终结符号集合之后。
如果没有交集,那么就是ϵ−NFA\epsilon-NFAϵ−NFA的F啦。
ϵ−NFA\epsilon-NFAϵ−NFA 和 NFA转化的例子
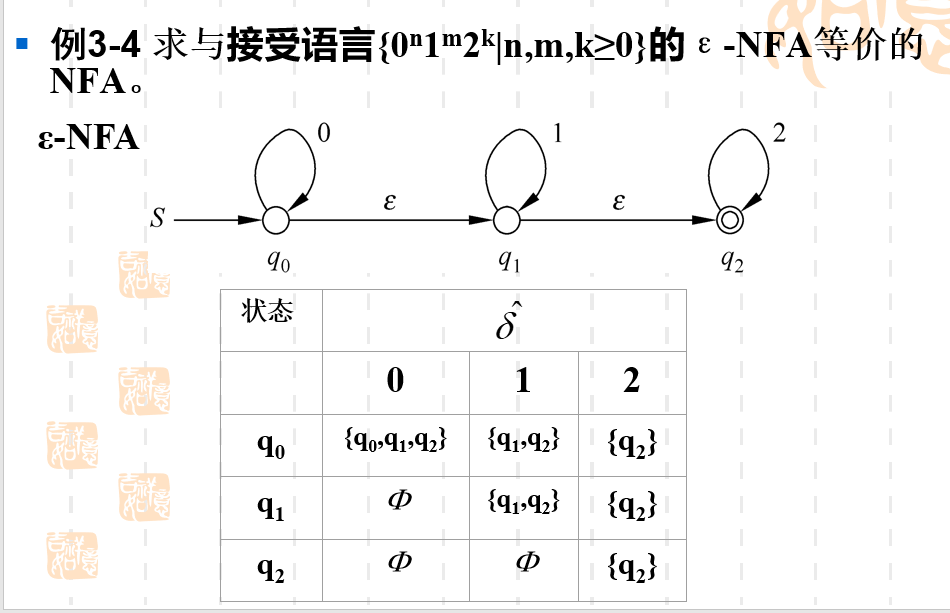
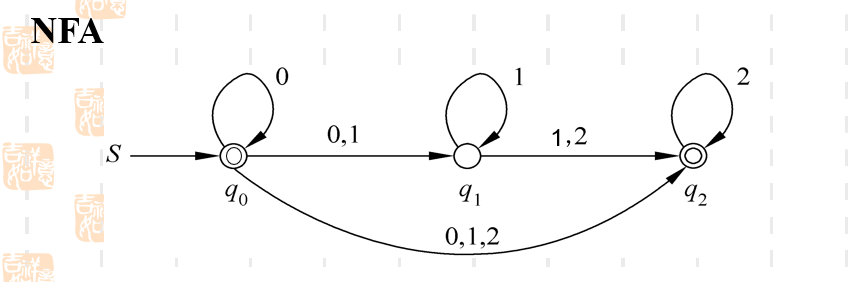
小总结
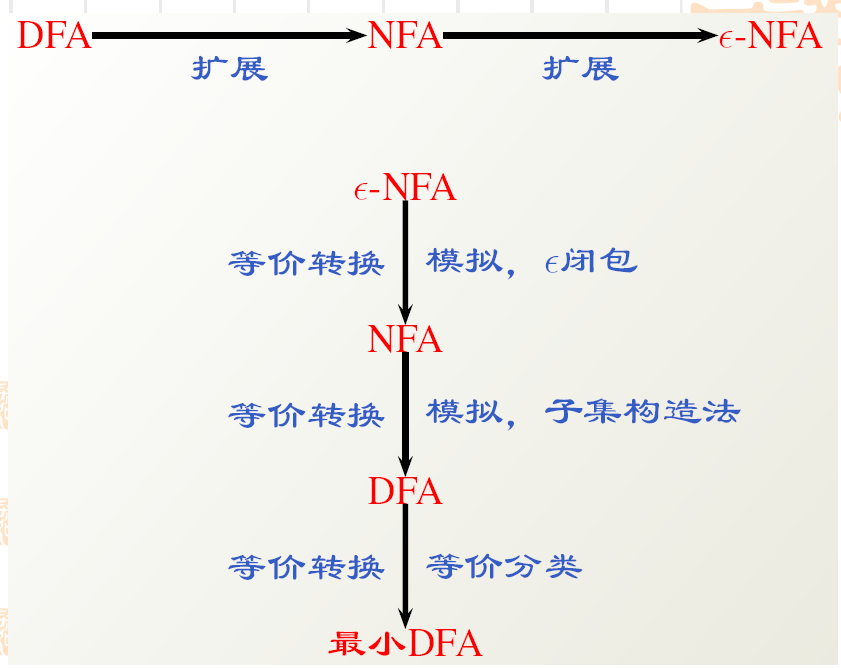
在实现一个具体FA的时候,我们可以先写出最简单,最智能,最容易写的ϵ−NFA\epsilon-NFAϵ−NFA,然后通过等价转化,转化为我们需要的NFANFANFA获得DFADFADFA。
定理3-3
FA接收的语言是正则语言。

这里你可能已经忘记正则语言的定义了,正则语言是正则文法,即3型文法产生出的语言。3型文法有3个特点,首先产生式右侧的长度大于等于左侧的长度(确保是一个1型文法),然后产生式左侧一定是语法变量,而且一定是一个,不能多也不能少(确保是一个2型文法)。然后产生式右侧最好就只有终结符,如果有语法变量的话,只能出现在最后。
从FA得到等价的正则文法的例子1
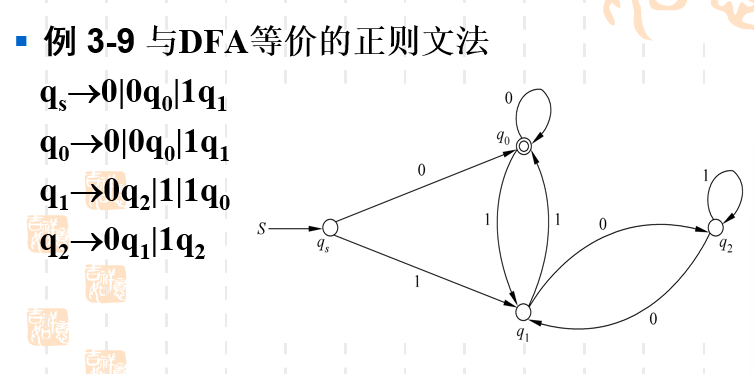
我们可以看到,文法的产生式实际上就是去看这个DFA的图。比如qsq_sqs有两条路径,分别为接收0后转化为q0q_0q0,和接收1后转化为q1q_1q1。所以就可以写出产生式qs→0q0∣1q1q_s \rightarrow0q_0|1q_1qs→0q0∣1q1。然后因为接收0后转到的q0q_0q0是一个终结状态,所以还需要把qs→0q_s\rightarrow 0qs→0加入产生式。故最后的产生式就是qs→0q0∣1q1∣0q_s \rightarrow0q_0|1q_1|0qs→0q0∣1q1∣0。
从FA得到等价的正则文法的例子2
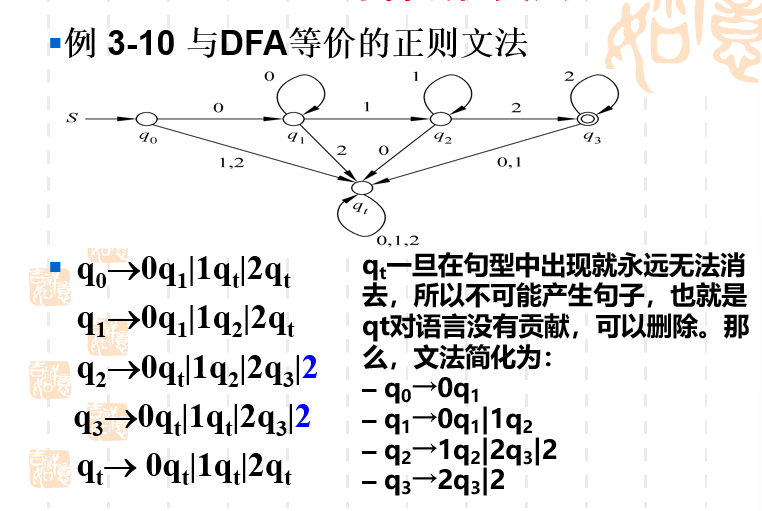
相信你已经能很快写出了DFA等价的正则文法了。在这个例子中由于陷阱状态qtq_tqt对语言没有贡献,可以进行简化,实际上就是把所有有qtq_tqt的地方进行删除。
定理3-4
正则语言可以由FA接受。


给定正则文法求等价FA的例子
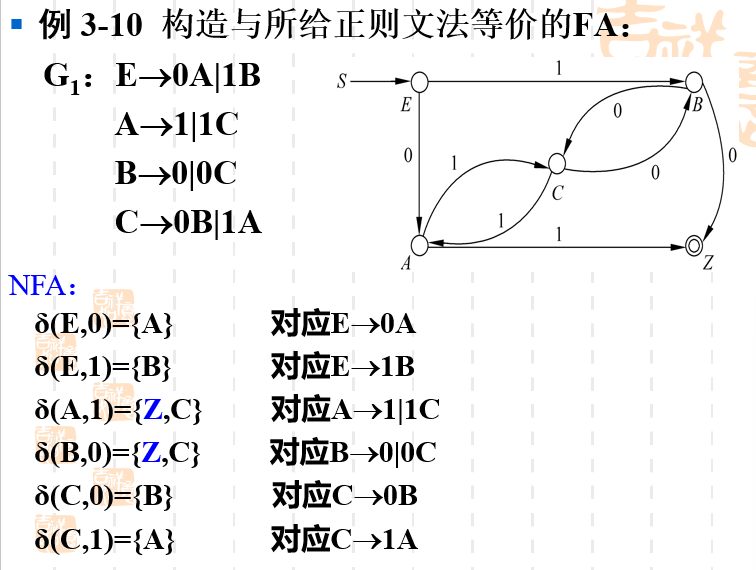
直接看答案应该能够很容易理解。如果产生式中有终结符,那么转移符号中需要写Z。
推论3-1 FA与正则文法等价
通过定理3-3和定理3-4就可以得到。
给定一个FA就能求出一个等价的正则文法。 给定一个正则文法就能求出等价的FA
FA与左线性文法
之前讲的正则文法实际上是右线性文法,因为正则文法的产生式右侧的语法变量是在最右边的。
而如果产生式右侧的语法变量在最左侧,那就是左线性文法了。它和FA有什么关系呢?


因为左线性文法利用了规约,所以对应对应出来的FA就像反了一样。
FA的起点实际上是左线性文法的终点。FA的终点实际上是左线性文法的起点。FA过了一遍,让一个语言从终结符号们变成了开始符号。实际上这就是规约的过程。
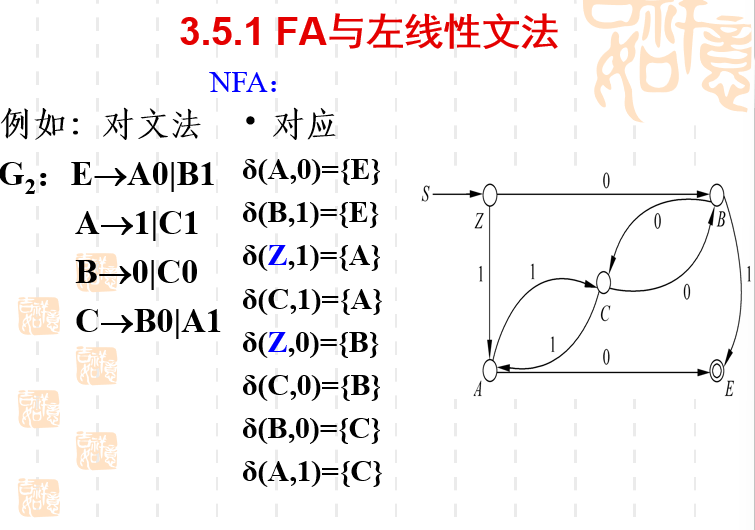


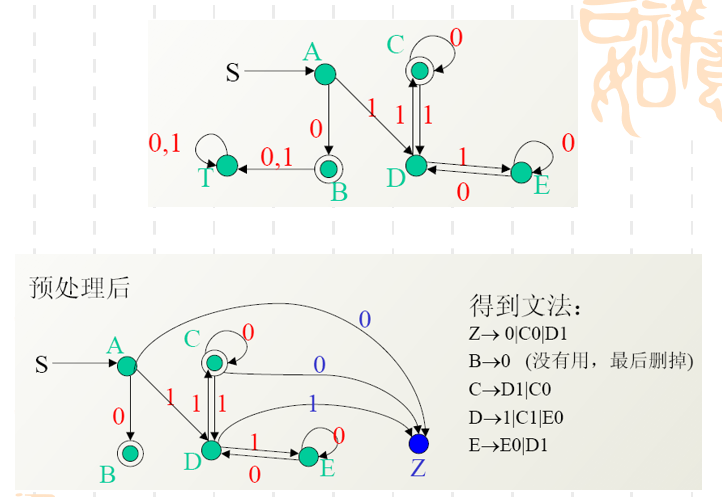
定理3-5
左线性文法和FA等价
第四章——正则表达式
正则文法擅长语言的产生。有穷状态自动机擅长语言的识别。
这里又有一个新的概念,正则表达式,它不是文法也不是有穷状态自动机,它是对正则语言的一种描述。它非常简洁,也更加像语言。
定义
正则表达式 regular expression RE
- ϕ\phiϕ是∑\sum∑的RE,它表示语言ϕ\phiϕ
- ϵ\epsilonϵ是∑\sum∑的RE,它表示语言{ϵ}\{\epsilon\}{ϵ} 从以上两个定义我们也回顾到一个事实,语言是一个集合
- 对于∀a∈∑\forall a\in \sum∀a∈∑,a是∑\sum∑上的RE,它表示语言{a}\{a\}{a}
- 如果r和s分别是∑\sum∑上表示语言R和S的RE,则 r与s的和 (r+s)是∑\sum∑上的RE,(r+s)表示的语言为R∪SR\cup SR∪S r与s的乘积 (rs) 是∑\sum∑上的RE,(rs)表达的语言为RS r的克林闭包(r∗)(r^*)(r∗)是∑\sum∑上的RE,(r∗)(r^*)(r∗)表达的语言为R∗R^*R∗
- 只有满足1,2,3,4的才是∑\sum∑上的RE
例子
设∑={0,1}\sum=\{0,1\}∑={0,1}
- 0 表示语言{0}\{0\}{0}
- 1 表示语言 {1}\{1\}{1}
- (0+1)(0+1)(0+1)表示语言{0,1}\{0,1\}{0,1} 语言{0,1}\{0,1\}{0,1}表示这个语言中有两个合法句子(不考虑空串),分别为0和1。
- (01) 表示语言{01}\{01\}{01}
- ((0+1)∗)((0+1)^*)((0+1)∗) 表示语言{0,1}∗\{0,1\}^*{0,1}∗
- ((00)((00)∗))((00)((00)^*))((00)((00)∗)) 表示语言{00}{00}∗\{00\}\{00\}^*{00}{00}∗ 两个语言相乘
约定
- r的正闭包r+r^+r+表示r与(r∗)(r^* )(r∗)的乘积以及(r∗)(r^*)(r∗)与r的乘积 r+=(r(r∗))=((r∗)r)r^+=(r(r^* ))=((r^* )r)r+=(r(r∗))=((r∗)r)
- 闭包运算的优先级最高,乘运算的优先级次之,加运算的优先级最低。所以在乘法明确时,可以使用省略一些括号。
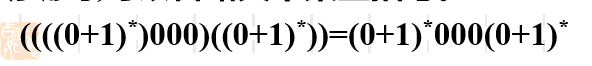
- 在意义明确时,RE,r表示语言记为L(r)L(r)L(r),也可直接记为r。
- 加 乘 闭包运算均执行左结合规则。
相等的定义
如果两个正则表达式产生的原因是相同的,则称两个正则表达式相等或者等价。
基本结论



RE与FA等价
正则表达式r成为FA M等价,如果L(r)=L(M)L(r)=L(M)L(r)=L(M)
实际上就是两者产生的语言若是相同的,就叫做等价了
RE到FA等价变化的例子
这里貌似遵循了ϵ−NFA\epsilon-NFAϵ−NFA要将多个终结状态转移到一个上的规定
定理4-1
RE表示的语言是RL。
个人感觉这个定理的证明反而不重要,而我们需要记住一些RE对应的FA。
- 若没有任何运算符,即没有加法、乘法或者闭包 的FA
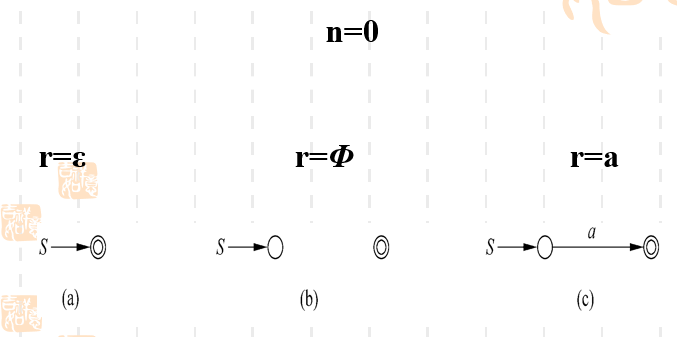
从这里我们可以看到空串和空集的区别。如果一个语言中包含空串,那么相当于空串是一个合法的句子,即不用读入任何输入字符就可以得到一个合法的句子,到了接受状态。 而如果一个语言是一个空集,相当于你无论接受什么输入字符,都不会到达接受状态,相当于这个语言不接受任何句子。即它的接受状态是孤立无援的。
- 若两个正则表达式相加 的FA
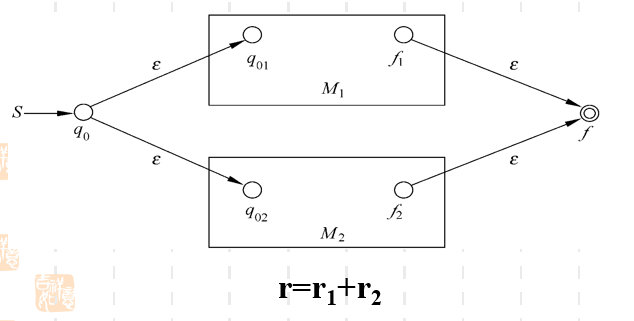
RE相加实际就是语言相交,即这个语言的某个句子是接受的,那个语言的某个句子也是接受的,所以我们可以从图中看到,本来两个语言的终止状态f1f_1f1和f2f_2f2现在同时指向了新的接受状态fff。
- 若两个正则表达式相乘 的FA
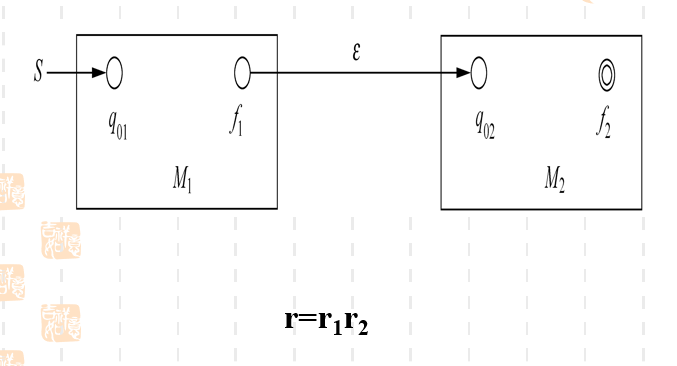
相乘需要这个语言中取一个句子,那个语言中取一个句子,即笛卡尔乘积。最终拼接形成的新的句子是被接受的。
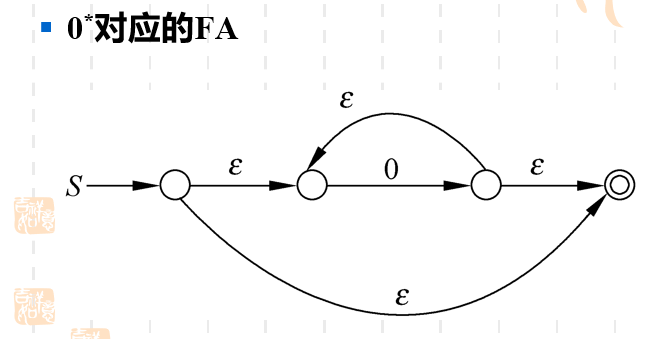
- 正则表达式的克林闭包
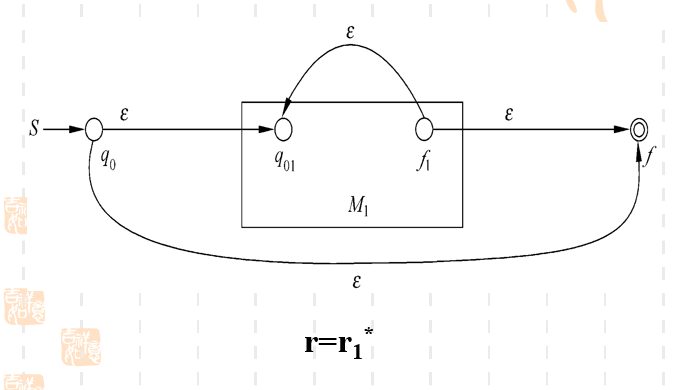
可能直接从开始状态直接到接受状态,因为克林闭包包含空串 也可能在读入无数个字符。
定理4-2
RL可以用RE来表示。
我们先来看一下一个用RE来表示一个RL的实际例子。
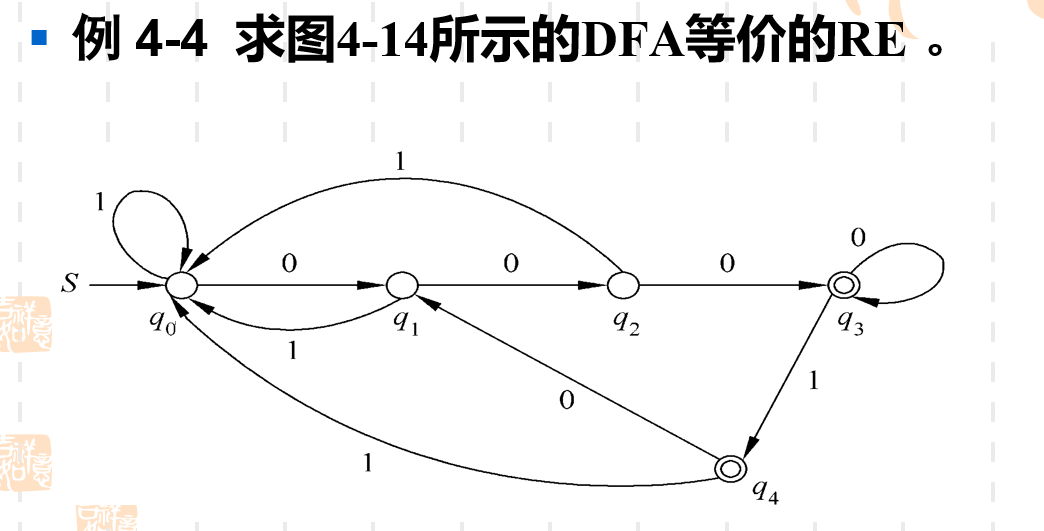

我们可以看到一个由DFA描述的正则语言最后可以用一串正则表达式来表示。
下面我们利用“图上作业法”一步一步将DFA进行转化,得到最后的正则表达式。
- 首先我们需要对DFA进行预处理。
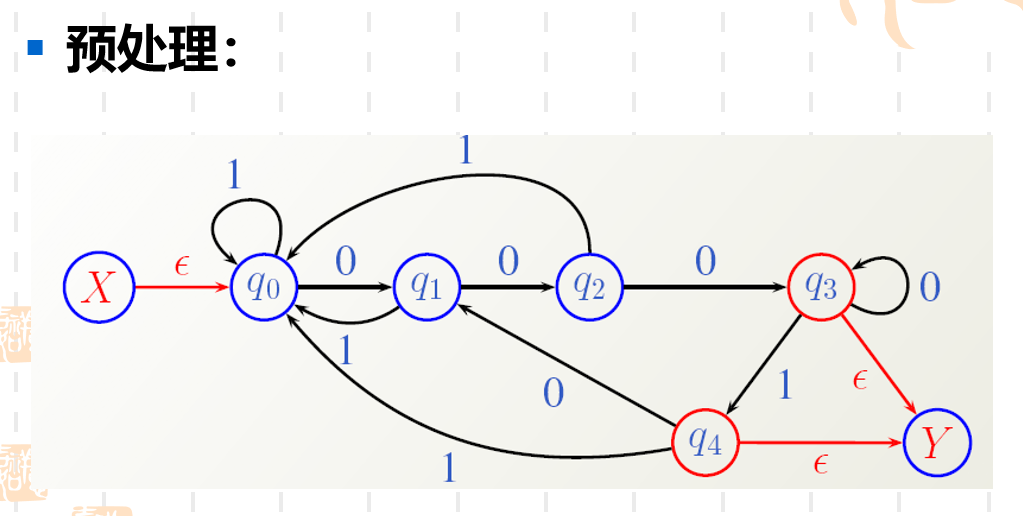
我们看到预处理干的时期实际上就是用一个X状态指向原来的初始状态q0q_0q0。然后将原来的两个终止状态q3q_3q3和q4q_4q4指向状态Y。这些指向都用ϵ\epsilonϵ来转移。 如果原本的DFA中有不可达状态的话,还还需要在预处理中直接去掉不可达状态(从初始状态无法到达的状态叫做不可达状态)
- 然后需要对预处理后的图进行一系列循环操作,这里操作主要分为并弧和去状态。
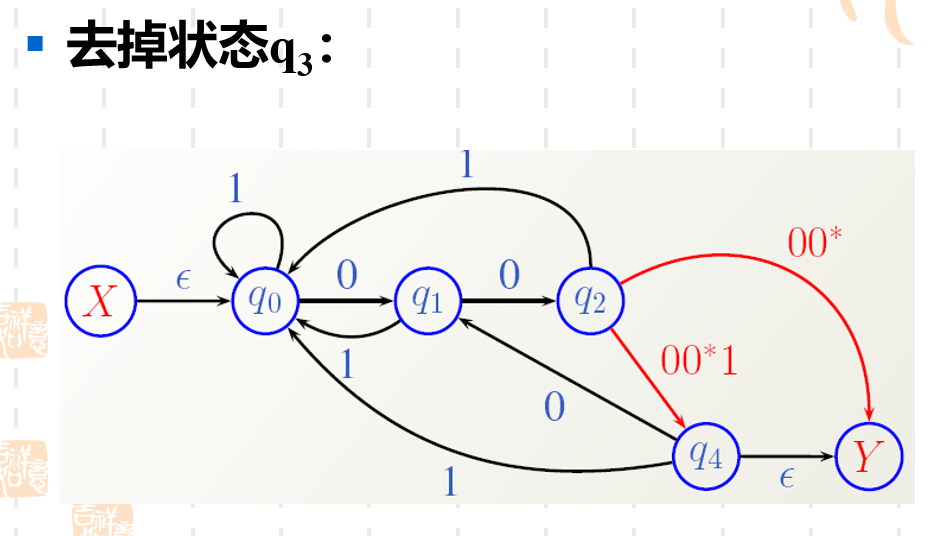
直接把q3q_3q3去掉了,所以以前经过q3q_3q3的顶点的弧需要重新进行指向。 比如之前q2q_2q2可以通过q3q_3q3到达YYY状态和q4q_4q4状态。现在q3q_3q3没有了,需要q2q_2q2来直接指向YYY和q4q_4q4。 然后弧上直接用正则表达式来表示,比如q2q_2q2经过q3q_3q3到达YYY的时候,q3q_3q3可能会进行自转,这里用的是0∗0^*0∗的正则表达式来表示。
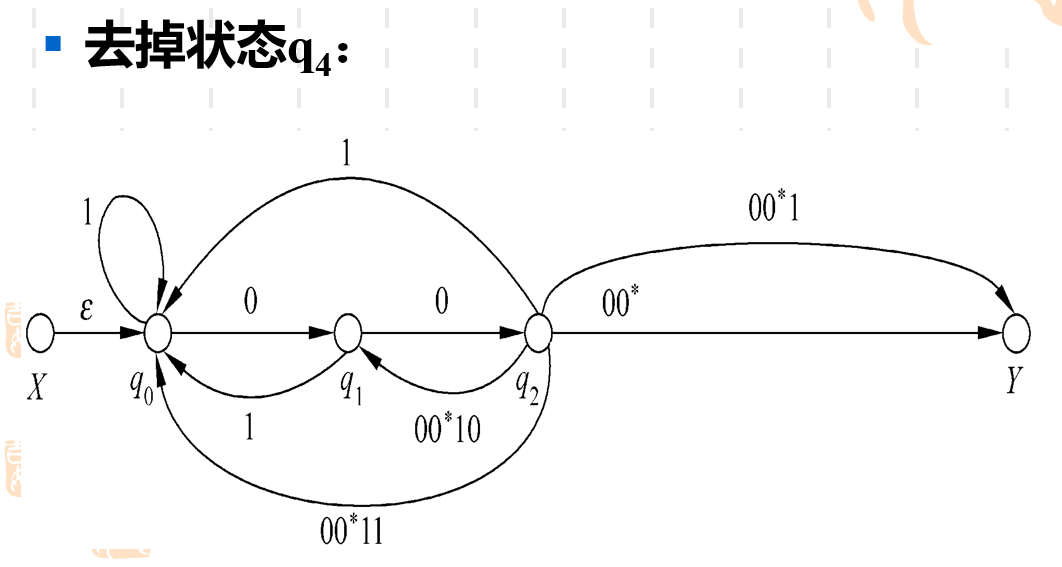
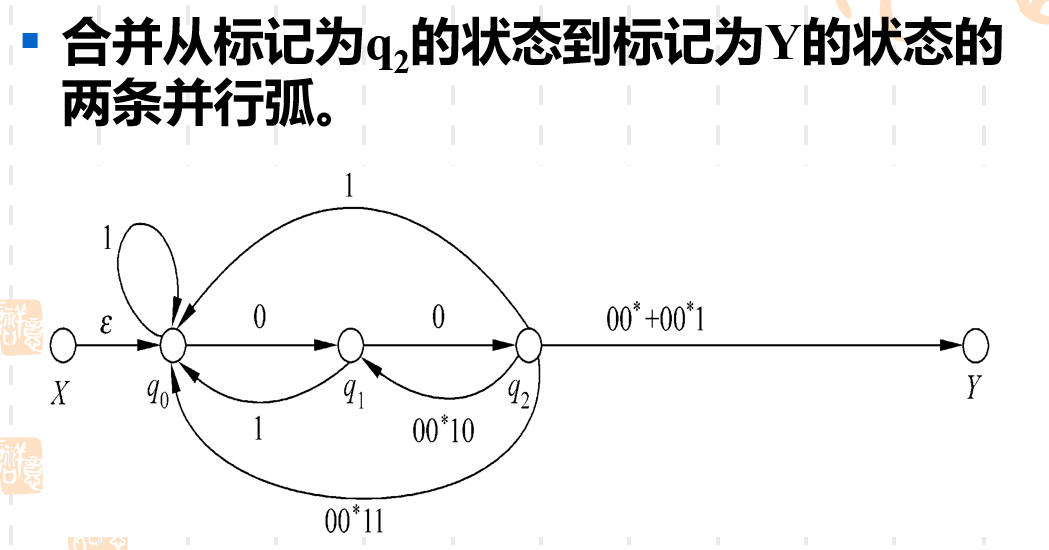
之前去掉状态q3q_3q3和q4q_4q4都属于“去状态”的操作。这里我们遇到了第二种操作“并弧”。实际很简答, 如果两个状态之间有两条并行的弧,可以用正则表达式中的"+"来进行合并。
接下来就是同样的操作了,实际上你去状态的顺序和并弧的顺序可以任意,看哪个状态不顺眼就去它。一直循环往复,最后剩下X到Y只有一条弧的时候,工作就结束了,弧上的正则表达式就是我们最后的结果。
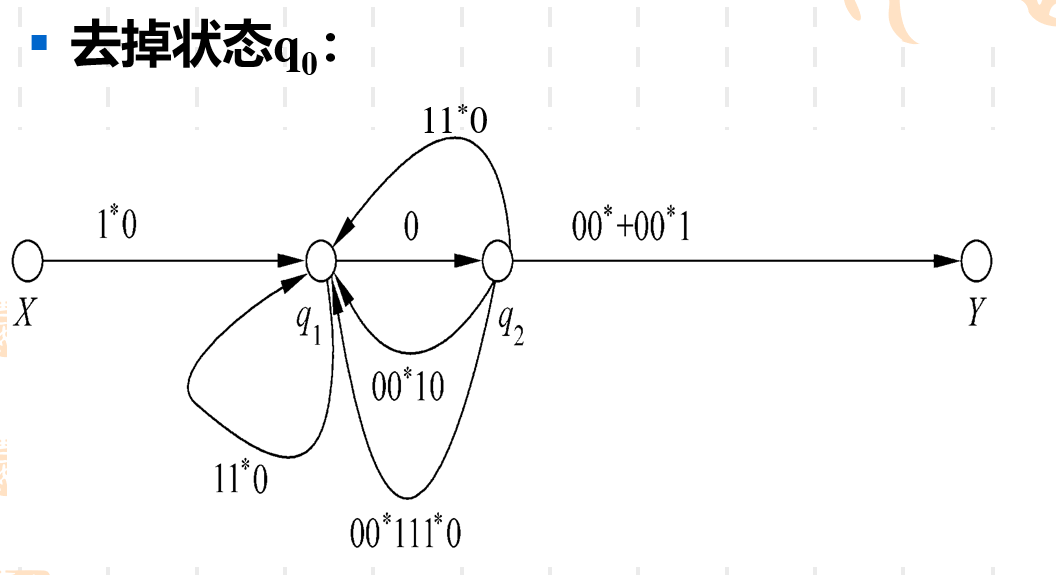
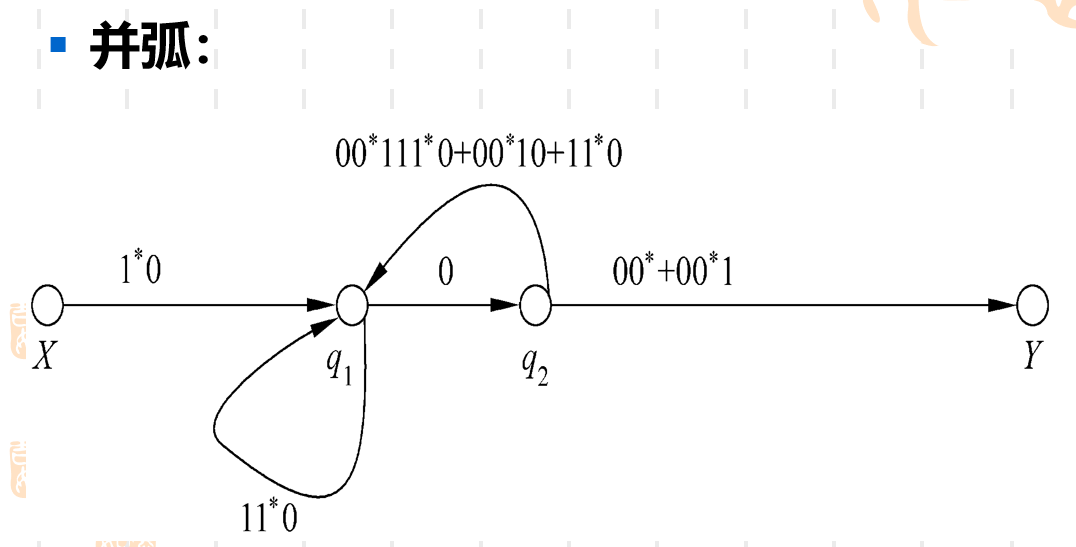
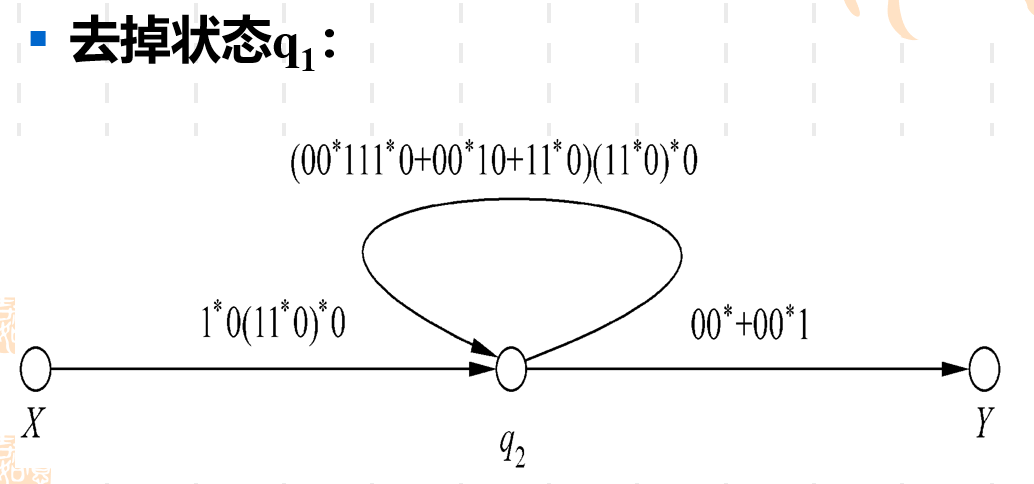

值得注意的是,因为在过程中选择哪个状态去除以及那两条边与合并,这里每个人的顺序可能会不一样,这就会导致最终的正则表达式在形式上看起来是不同的,但是实际上它们都是等价的。
如果化到最后发现X无法到达Y,我们认为它的正则表达式是ϕ\phiϕ
推论4-1
正则表达式与FA、正则文法等价,是正则语言的表示模型