编码生成矩阵与检错监督矩阵

timerring

发布于 2023-06-16 15:27:40

7970

文章被收录于专栏：TechBlogTechBlog

线性分组码

例:(7,3)线性分组码

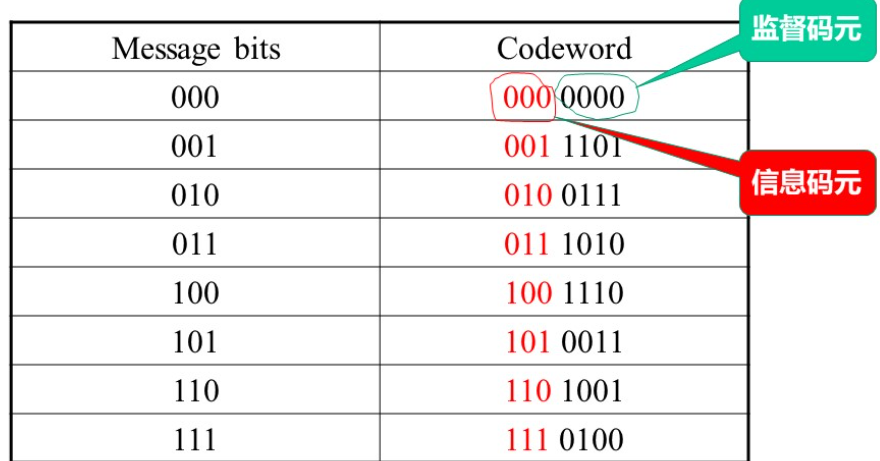
编码-生成矩阵

编码和生成矩阵

（n，k ）线性分组码的构造——依据给定的 k 个信息码元，设计满足编码条件（最小码距、码率）的 n-k个监督码元。

例: 二元 (7,3) 线性分组码, n=7, k=3, r=7-3=4 ,

\mathbf{u}=\left(u_{2}, u_{1}, u_{0}\right) \rightarrow \mathbf{c}=\left(c_{6}, c_{5}, c_{4}, c_{3}, c_{2}, c_{1}, c_{0}\right)

构造:

编码位高位直接对应信息位;

编码位低位由信息位组合而成。.

\begin{array}{ll} c_{6}=u_{2} & c_{3}=u_{2} \bigoplus u_{0}=c_{6} \oplus c_{4} \\ c_{5}=u_{1} & c_{2}=u_{2} \bigoplus u_{1} \oplus u_{0}=c_{6} \oplus c_{5} \oplus c_{4} \\ c_{4}=u_{0} & c_{1}=u_{2} \bigoplus u_{1}=c_{6} \oplus c_{5} \\ & c_{0}=u_{1} \oplus u_{0}=c_{5} \oplus c_{4} \end{array}

写成矩阵形式，为

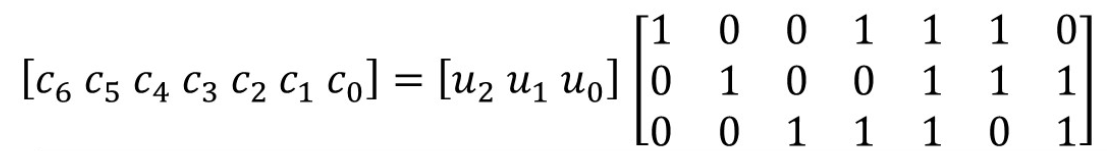
求非系统 (7,4) 线性分组码的等价系统码生成矩阵。

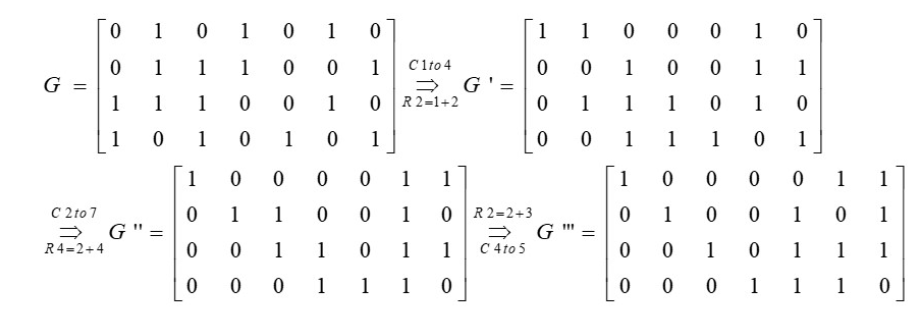
\mathrm{G}=\left[\begin{array}{lllllll} 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 1 \end{array}\right]

列的交换和初等行变换不改变矩阵的秩，变换后矩阵的各行矢量仍线性无关。 任何一个线性分组 (n, k)码都可等价于一个系统码。（纠错能力、编码结构) 思考:由非系统型生成矩阵变换成系统型生成矩阵，答案唯一吗?

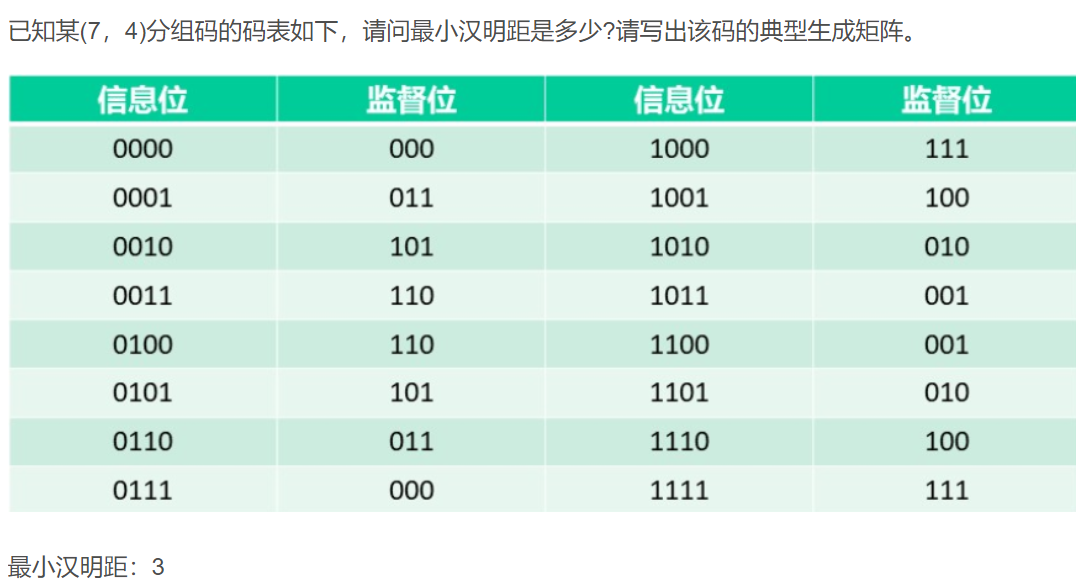
已知某(7，4)分组码的码表如下，请问最小汉明距是多少?请写出该码的典型生成矩阵。

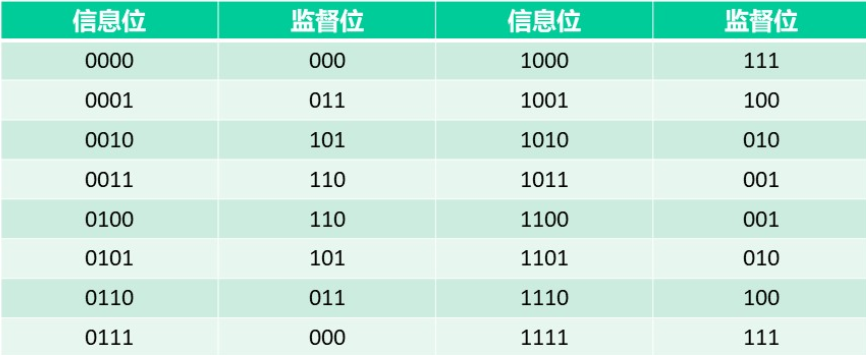
最小汉明距：3

生成矩阵:

G=\left[\begin{array}{lllllll} 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 \end{array}\right]

检错-监督矩阵

由分组码的生成矩阵可得到其监督矩阵。

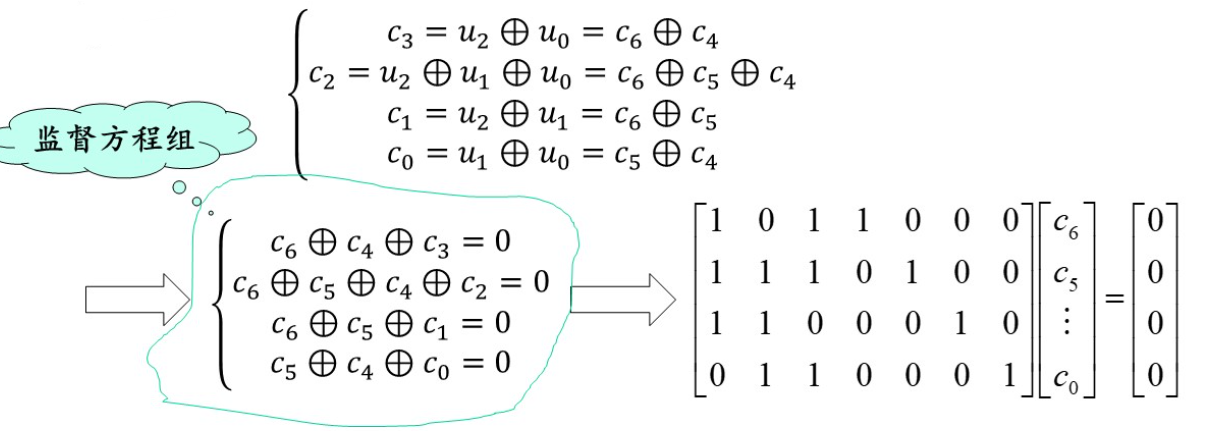
\mathbf{H C}^{T}=\mathbf{0}^{T},[\mathbf{P}: \mathbf{I}] \mathbf{C}^{T}=\mathbf{0}^{T}

一般情况下, 一个 (n, k) 线性分组码的H矩阵中的（n-k）行对应（n-k）个线性监督方程组, 以确定（n-k）个监督码元。

\mathbf{H}

——线性分组码的监督矩阵，是

（n-k） \times \mathbf{n}

阶的。

若 H=[P ：I], 其中 I 是 ( n-k ）阶方阵, 则 H 为典型监督矩阵。

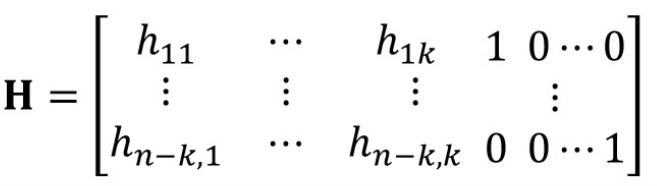
监督矩阵的特性

参考文献：

Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2023-06-13，如有侵权请联系 cloudcommunity@tencent.com 删除

编码