最强总结!8个线性回归核心点!!
最强总结!8个线性回归核心点!!

核心点:8 个线性回归核心要点总结!
很多初学者,从机器学习开始的那一刻,必须是先把线性回归搞定。
基本原理方面,其实比较简单,但是如果完整的来论述的话,东西还是需要捉摸几天的。
那从今天开始,我预计会陆陆续续出一些内容,来论述各个算法的基础核心点,大家感兴趣可以关注起来。
先来简单聊聊线性回归,线性回归作为一种简单而有效的建模方法,在数据分析、机器学习和统计学中非常重要,可用于预测与推断,提供了可解释性强、基础假设明确的模型框架,同时也为特征工程和其他复杂模型提供了基础。
今天咱们总结了关于线性回归的 8 个方面内容。
- 线性关系假设
- 参数估计
- 评估指标
- 多元线性回归
- 特征选择
- 正则化技术
- 模型诊断
- 预测与推断
下面,咱们从这 8 个方面,详细的把每一部分都论述一遍。
老规矩:大家伙如果觉得近期文章还不错!欢迎大家点个赞、转个发~
有其他补充,大家评论区可以讨论,或者留言~
咱们开始吧~
1. 线性关系假设
线性回归假设自变量和因变量之间存在线性关系,即因变量可以通过自变量的线性组合来表示。
理解线性关系假设是理解线性回归算法的关键之一。在解释这一点时,可以从基本概念开始,然后深入讨论其在实际应用中的意义和限制。
线性关系基础概念
线性关系是指两个或多个变量之间的关系可以用直线来描述。在线性回归中,假设因变量
和自变量
之间存在着线性关系。
这种关系可以表示为:
其中:
是因变量(要预测的变量);
是自变量(特征或解释变量);
是截距(模型的偏置);
是自变量的系数(模型的斜率);
是误差项,表示模型无法解释的随机误差。
线性关系的意义
线性关系假设的核心意义在于简化建模过程并提高可解释性。通过假设因变量和自变量之间的关系是线性的,可以用一个简单的线性方程来建模数据。这种简单性使得模型的理解和解释更为直观,使得可以更容易地理解自变量对因变量的影响。
另外,线性关系假设也使得使用最小二乘法等优化技术来估计模型参数成为可能。这些技术要求模型具有一定的数学形式,而线性关系正好提供了这种形式。
线性关系的限制
尽管线性关系假设在许多情况下是合理的,但在实际应用中,很多情况下因变量和自变量之间的关系并不总是线性的。例如,如果因变量和自变量之间存在非线性关系,那么线性模型可能无法很好地拟合数据。
此外,线性关系假设还要求误差项
是独立同分布的,并且具有常量的方差。如果这些假设不成立,可能会导致模型的预测效果不佳。
如何检验线性关系假设
在应用线性回归模型之前,通常需要对线性关系假设进行检验,以确保模型的合理性。
常用的方法有:
- 观察因变量和自变量之间的散点图,查看是否存在明显的线性关系;
- 分析残差图,检查残差是否随着预测值的变化而随机分布;
- 进行统计检验,如F检验或t检验,检验自变量的系数是否显著不为零。
如何处理非线性关系
当因变量和自变量之间存在非线性关系时,可以通过以下方法来处理:
- 变量转换:对自变量或因变量进行变换,使其更接近线性关系,如对数变换、平方根变换等;
- 添加高阶项:在模型中添加自变量的高阶项,如
等,以捕捉非线性关系;
- 使用非线性模型:考虑使用其他类型的模型,如多项式回归、广义加性模型(GAM)等,来适应非线性关系。
综上,线性关系假设是线性回归算法的核心之一,它使得建模过程更加简单和可解释。
然而,在实验中,需要谨慎地检验这一假设,并在必要时采取适当的方法来处理非线性关系,以确保模型的准确性和可靠性。
2. 参数估计
通过训练数据集,线性回归算法估计模型的参数,其中最常见的方法是最小二乘法(Ordinary Least Squares,OLS),目标是最小化实际观测值与模型预测值之间的残差平方和。
参数估计是线性回归算法中至关重要的一步,它涉及到如何通过训练数据集来确定模型的参数,使得模型能够最好地拟合数据。
其中,最常见的方法是最小二乘法(Ordinary Least Squares,OLS)。
最小二乘法原理
最小二乘法 通过最小化实际观测值与模型预测值之间的残差平方和来估计模型的参数。残差是每个观测值与其对应的预测值之间的差异,残差平方和是所有残差的平方的总和。
OLS的目标是选择参数值,使得这个残差平方和尽可能地小。
求解参数的步骤
使用最小二乘法求解线性回归模型的参数通常包括以下步骤:
- 定义模型: 首先,需要定义线性回归模型的数学形式,即
,其中
是因变量,
是自变量,
是模型的参数,
是误差项。
- 确定损失函数: 损失函数是用来衡量模型预测值与实际观测值之间的差异的函数。在最小二乘法中,通常使用残差平方和作为损失函数。
- 最小化损失函数: 使用优化算法(通常是梯度下降法或闭式解)来最小化损失函数。在最小二乘法中,要找到使得残差平方和最小的参数值。对于线性回归模型,可以通过求解以下正规方程(normal equations)来得到闭式解:
其中,
是自变量的设计矩阵,
是因变量的观测值,
是参数向量。
OLS方法的特点与优缺点
优点:
- 简单直观:OLS提供了一种直观且易于理解的方法来估计模型参数。
- 全局最优解:在一些情况下,OLS可以得到模型的全局最优解。
- 闭式解:对于小型数据集,可以直接使用闭式解来计算参数,而无需使用迭代优化算法。
缺点:
- 对异常值敏感:OLS对异常值比较敏感,因为它会直接受到异常值的影响,导致参数估计的偏差。
- 计算复杂度高:当数据集较大时,计算正规方程的逆矩阵可能会变得非常耗时,甚至不可行。
- 对多重共线性的处理:在存在多重共线性(自变量之间存在高度相关性)的情况下,OLS的估计结果可能不稳定,需要额外的处理方法。
参数估计的评价
在进行参数估计后,通常需要对估计结果进行评价,以确保模型的可靠性和有效性。
评价参数估计的常用方法包括:
- 残差分析: 分析残差的分布和模式,检验模型的拟合效果和误差项的假设是否成立。
- 参数显著性检验: 使用统计检验方法(如t检验)来检验参数估计的显著性,判断自变量与因变量之间是否存在显著的线性关系。
- 模型拟合度评估: 使用拟合度指标(如R-squared、调整R-squared等)来评估模型的拟合程度,判断模型对数据的解释能力。
参数估计决定了模型对数据的拟合程度和预测能力。通过最小二乘法,可以有效地估计模型的参数,并通过各种评价方法来验证模型的有效性。然而,在应用中需要注意参数估计的局限性,并结合实际情况进行适当的调整和处理,确保模型的准确性和可靠性。
3. 评估指标
用于评估模型性能的指标包括:
- 均方误差(Mean Squared Error,MSE)
- 均方根误差(Root Mean Squared Error,RMSE)
- 平均绝对误差(Mean Absolute Error,MAE)等
评估指标是用来衡量模型预测结果与真实观测值之间的差异程度,从而评估模型的性能。
在线性回归中,常用的评估指标包括均方误差(MSE)、均方根误差(RMSE)和平均绝对误差(MAE)。
均方误差(MSE)
均方误差是预测值与真实值之间差异的平方的平均值:
其中:
是样本数量;
是第
个观测值的真实值;
是第
个观测值的预测值。
均方根误差(RMSE)
均方根误差是均方误差的平方根,用来衡量预测值与真实值之间的平均偏差:
平均绝对误差(MAE)
平均绝对误差是预测值与真实值之间差异的绝对值的平均值:
推导过程
这些评估指标的推导过程可以通过最小化某些损失函数来实现。以均方误差为例,可以通过最小化残差平方和来得到参数的估计值。
具体地,在线性回归中,的目标是最小化残差平方和:
其中
是真实值,
是预测值。通过最小化 RSS,可以得到最优的模型参数估计值。
应用场景
- 均方误差(MSE): 适用于评估模型对异常值的敏感程度。由于MSE计算了预测值与真实值之间的平方差,因此对大的误差给予较大的惩罚,使得模型更加关注这些大误差,适用于需要关注所有预测误差的场景。
- 均方根误差(RMSE): 将均方误差进行平方根处理后得到的指标,具有与原始数据相同的量纲,更直观地反映了预测值与真实值的平均偏差,常用于解释模型的预测误差的平均水平。
- 平均绝对误差(MAE): 对预测值与真实值之间的绝对差值进行求平均,不考虑差值的正负,因此更加稳健,不受异常值的影响,适用于对异常值敏感的场景。
总的来说,均方误差、均方根误差和平均绝对误差都是常用的评估指标,各有优缺点,实际情况中,要选择合适的指标来评估模型的性能。
4. 多元线性回归
多元线性回归是一种扩展了简单线性回归的模型,在考虑多个自变量的情况下建立与因变量之间的线性关系。
公式推导
多元线性回归模型的数学表达式为:
其中:
是因变量(要预测的变量);
是自变量(特征或解释变量);
是截距(模型的偏置);
是自变量的系数(模型的斜率);
是误差项,表示模型无法解释的随机误差。
参数估计过程
为了估计多元线性回归模型的参数,可以使用最小二乘法。首先,将模型的公式写成矩阵形式:
其中:
是因变量的观测值(
的列向量);
是自变量的设计矩阵(
的矩阵),其中第一列是全1向量,用来对应截距项;
是参数向量(
的列向量);
是误差项(
的列向量)。
接下来,的目标是最小化残差平方和
。将残差向量表示为
,可以得到最小二乘估计为:
下面,咱们写一个案例,大家可以进行理解~
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
np.random.seed(0)
X1 = 2 * np.random.rand(100, 1)
X2 = 3 * np.random.rand(100, 1)
X3 = 4 * np.random.rand(100, 1)
Y = 4 + 3*X1 + 5*X2 + 2*X3 + np.random.randn(100, 1)
# 使用sklearn进行多元线性回归拟合
X = np.concatenate((X1, X2, X3), axis=1)
model = LinearRegression()
model.fit(X, Y)
Y_pred = model.predict(X)
# 计算均方误差
mse = mean_squared_error(Y, Y_pred)
print("Mean Squared Error:", mse)
# 可视化
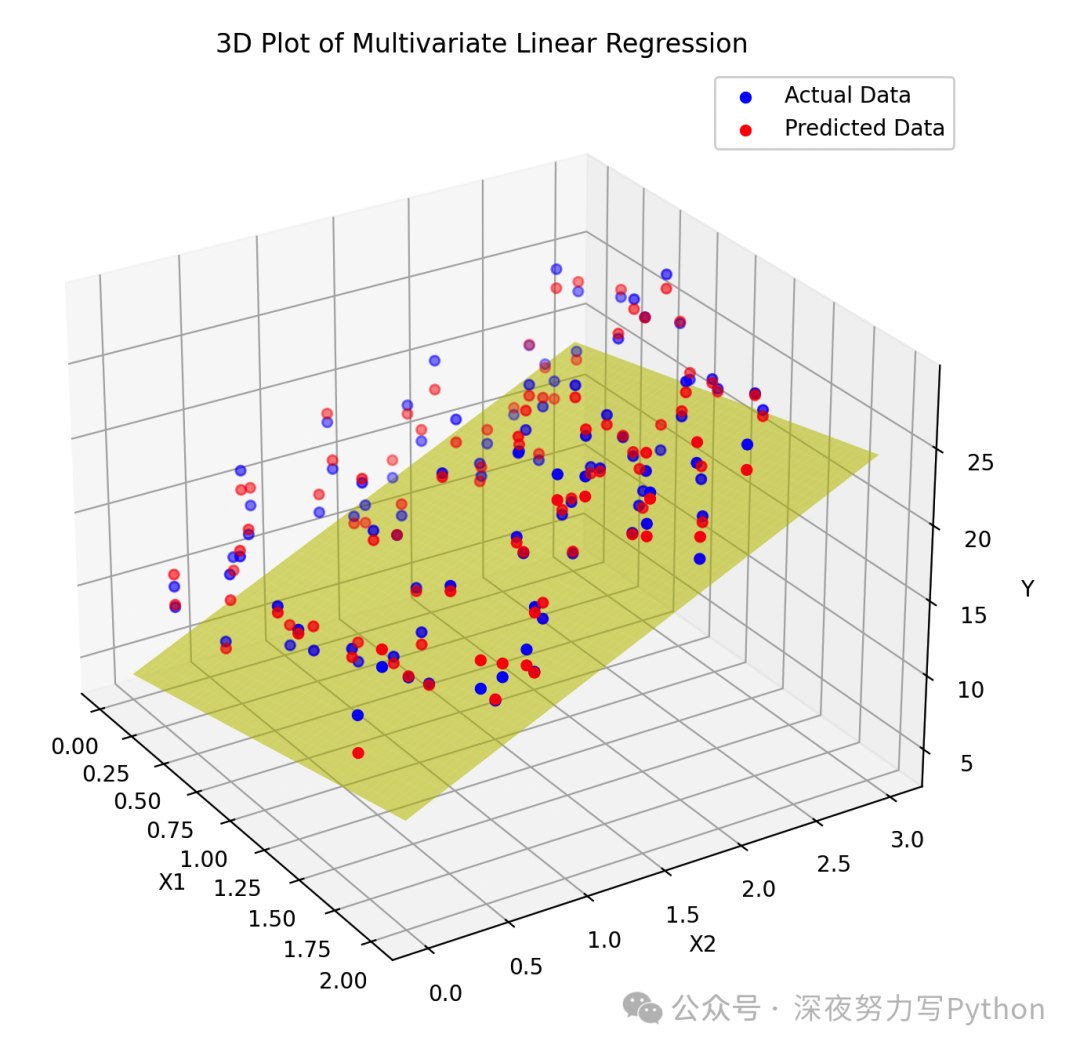
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X1, X2, Y, color='b', label='Actual Data')
ax.scatter(X1, X2, Y_pred, color='r', label='Predicted Data')
# 绘制平面
xx1, xx2 = np.meshgrid(np.linspace(0, 2, 100), np.linspace(0, 3, 100))
yy = model.intercept_ + model.coef_[0][0]*xx1 + model.coef_[0][1]*xx2
ax.plot_surface(xx1, xx2, yy, alpha=0.5, color='y')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('Y')
ax.set_title('3D Plot of Multivariate Linear Regression')
plt.legend()
plt.show()
代码最开始,生成了具有3个自变量的样本数据,然后添加了一些随机误差。
接着,使用LinearRegression模型从样本数据中拟合出多元线性回归模型,并输出了参数估计值。
5. 特征选择
特征选择 可以帮助从大量的自变量中挑选出最具影响力的变量,以提高模型的预测性能、减少过拟合的风险并简化模型的解释。
咱们直接举一个案例,通过特征选择来提高线性回归模型的性能,最后通过可视化可以看看效果~
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# 生成样本数据
np.random.seed(0)
n_samples = 100
n_features = 5
X = np.random.rand(n_samples, n_features) # 生成自变量
coefficients = np.random.rand(n_features) # 真实的系数
intercept = 2.5 # 截距
epsilon = 0.1 * np.random.randn(n_samples) # 生成误差项
Y = intercept + np.dot(X, coefficients) + epsilon # 生成因变量
# 分割训练集和测试集
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
# 定义函数,用于评估模型的性能
def evaluate_model(X_train, X_test, Y_train, Y_test):
model = LinearRegression()
model.fit(X_train, Y_train)
Y_pred = model.predict(X_test)
mse = mean_squared_error(Y_test, Y_pred)
return mse, Y_pred
# 模型评估
all_features_mse, _ = evaluate_model(X_train, X_test, Y_train, Y_test)
print("MSE using all features:", all_features_mse)
# 选择不同的自变量组合进行建模
selected_features = [[0, 1], [1, 2, 3], [2, 3, 4]] # 不同的自变量组合
mse_values = []
for i, features in enumerate(selected_features):
X_train_selected = X_train[:, features]
X_test_selected = X_test[:, features]
mse, Y_pred = evaluate_model(X_train_selected, X_test_selected, Y_train, Y_test)
mse_values.append(mse)
# 可视化预测结果
plt.figure(figsize=(8, 6))
plt.scatter(Y_test, Y_pred, label=f'Features: {features}')
plt.plot([Y_test.min(), Y_test.max()], [Y_test.min(), Y_test.max()], 'k--', lw=2) # 对角线
plt.xlabel('True Values')
plt.ylabel('Predictions')
plt.title(f'True vs Predicted Values using Features: {features}')
plt.legend()
plt.show()
# 打印不同自变量组合的 MSE 值
for i, features in enumerate(selected_features):
print(f"MSE using selected features {features}: {mse_values[i]}")
# MSE using selected features [0, 1]: 0.07382629999218492
# MSE using selected features [1, 2, 3]: 0.0296225705109124
# MSE using selected features [2, 3, 4]: 0.03780369819446803
首先生成了包含5个自变量的样本数据集。然后,将数据集分割为训练集和测试集。接下来,定义了一个函数 evaluate_model 来评估模型的性能,并计算了模型在测试集上的均方误差(MSE)。
通过选择不同的自变量组合进行模型拟合,并打印了相应的 MSE 值。
最后,通过可视化展示了预测结果,比较了真实值和预测值之间的关系。
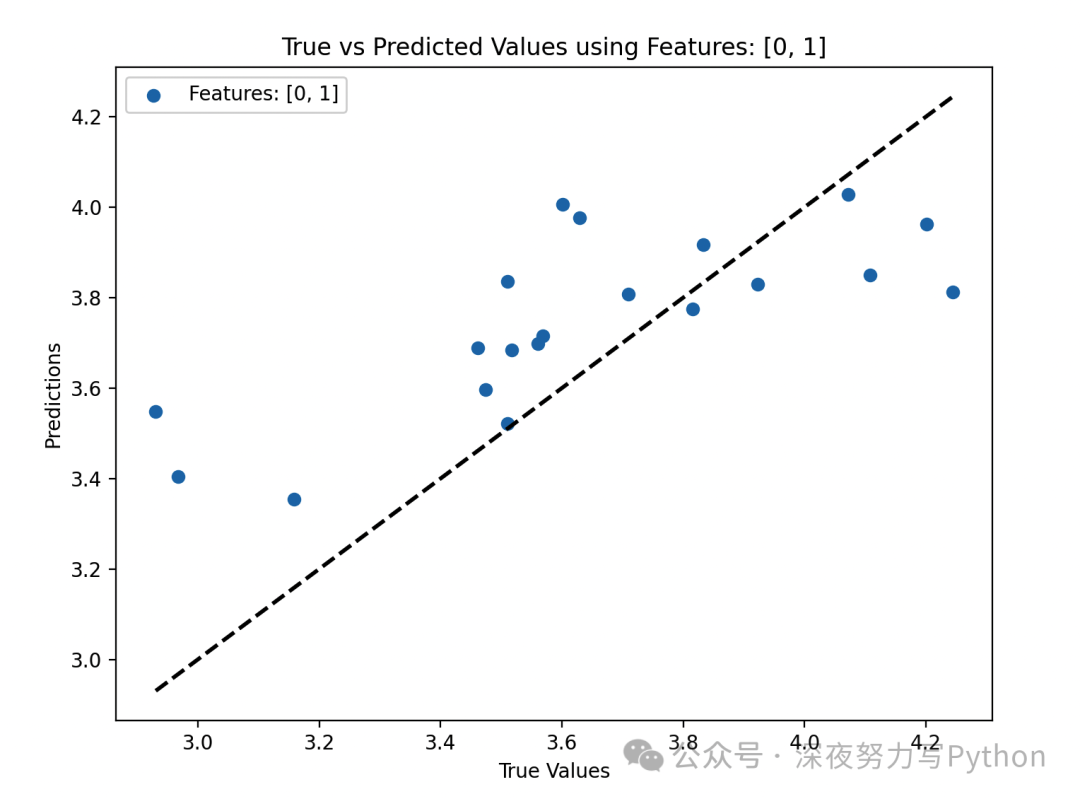
整个代码运行后,可以观察到选择不同的自变量组合对模型预测性能的影响,并通过可视化直观地展示了预测结果。这突显了特征选择在提高模型性能和预测准确度方面的重要性。
6. 正则化技术
为了防止过拟合,线性回归常常会使用正则化技术,如L1正则化(Lasso回归)和L2正则化(岭回归),以限制参数的大小或将某些参数置零。
正则化技术在机器学习中被广泛应用于控制模型的复杂度,避免过拟合问题。L1正则化(也称为Lasso回归)和L2正则化(也称为岭回归)是常用的正则化方法,它们分别通过添加L1范数和L2范数的惩罚项来限制模型参数的大小。
L1正则化(Lasso回归)
L1正则化通过添加参数向量的L1范数作为惩罚项,其优化目标可以表示为:
其中,
是均方误差(Mean Squared Error),
是正则化参数,控制正则化项的影响力,
是模型的第
个参数。
L2正则化(岭回归)
L2正则化通过添加参数向量的L2范数的平方作为惩罚项,其优化目标可以表示为:
其中,
是均方误差(Mean Squared Error),
是正则化参数,控制正则化项的影响力,
是模型的第
个参数。
下面,咱们再举一个案例,使用一个多项式函数作为目标函数,然后分别演示不使用正则化、使用L1正则化(Lasso回归)和使用L2正则化(Ridge回归)的情况。
代码中,生成一个具有噪声的多项式数据集,并拟合三种不同类型的模型。
最后,绘制一个拟合曲线以及观察它们之间的差异。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression, Lasso, Ridge
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_squared_error
# 生成多项式数据集
np.random.seed(0)
X = np.sort(5 * np.random.rand(50, 1), axis=0)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])
# 将特征进行多项式转换
degrees = [1, 4, 15] # 不同的多项式阶数
models = [('No Regularization', 'r', '-'),
('L1 Regularization (Lasso)', 'g', '--'),
('L2 Regularization (Ridge)', 'b', '-.')]
plt.figure(figsize=(14, 5))
for i, (name, color, linestyle) in enumerate(models):
ax = plt.subplot(1, len(models), i + 1)
plt.setp(ax, xticks=(), yticks=())
# 将特征进行多项式转换
polynomial_features = PolynomialFeatures(degree=degrees[i], include_bias=False)
if name == 'L1 Regularization (Lasso)':
model = make_pipeline(polynomial_features, Lasso(alpha=0.001))
elif name == 'L2 Regularization (Ridge)':
model = make_pipeline(polynomial_features, Ridge(alpha=0.1))
else:
model = make_pipeline(polynomial_features, LinearRegression())
# 拟合模型
model.fit(X, y)
y_pred = model.predict(X)
mse = mean_squared_error(y, y_pred)
# 绘制拟合曲线
plt.plot(X, y, color='cornflowerblue', linewidth=2, label="Ground Truth")
plt.plot(X, y_pred, color=color, linestyle=linestyle, linewidth=2,
label="{} (MSE: {:.2f})".format(name, mse))
plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(degrees[i], mse, 0.01), fontsize=14)
plt.xlabel("x", fontsize=14)
plt.ylabel("y", fontsize=14)
plt.legend(loc="best", fontsize=10)
plt.show()
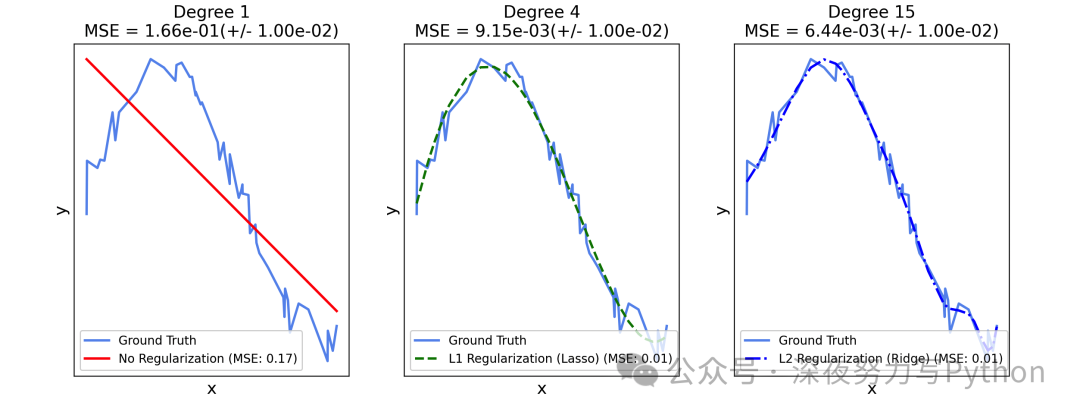
在这个案例中,使用了三种不同的模型来拟合数据:
- 不使用正则化:使用普通的线性回归模型来拟合数据。
- L1正则化(Lasso回归):使用Lasso回归来拟合数据,通过L1正则化惩罚项来限制参数的大小。
- L2正则化(Ridge回归):使用Ridge回归来拟合数据,通过L2正则化惩罚项来限制参数的大小。
对于每个模型,使用不同的多项式阶数进行拟合,分别为1、4和15。最后,绘制了拟合曲线,并标记了每个模型的均方误差(MSE)。
大家可以清晰地比较不同正则化方法和多项式阶数对拟合效果的影响。
7. 模型诊断
模型诊断的目标是检查模型是否满足建模假设,特别是残差的分布是否符合正态分布、是否存在异方差性等。
原理
- 残差分布是否符合正态分布: 在线性回归中,假设模型的残差(观测值与预测值之间的差异)应该是服从正态分布的。为了检查这一假设,可以绘制残差的直方图或Q-Q图,并观察是否近似于正态分布。
- 异方差性的检验: 异方差性指的是残差的方差随着自变量的变化而变化,即残差的方差不是恒定的。可以通过绘制残差与预测值的散点图,观察残差的方差是否随着预测值的变化而变化。如果残差的方差存在明显的模式,就可能存在异方差性。
- 多重共线性的检验: 多重共线性是指自变量之间存在高度相关性的情况,这可能导致模型估计的不稳定性和解释变量的解释性下降。可以计算自变量之间的相关系数,或者使用方差膨胀因子(VIF)来检验多重共线性的存在。
假设有一个简单的数据集,包含一个自变量
和一个因变量
,使用线性回归模型拟合这个数据集。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# 生成样本数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
Y = 4 + 3 * X + np.random.randn(100, 1) # 加入随机噪声
# 拟合线性回归模型
model = LinearRegression()
model.fit(X, Y)
Y_pred = model.predict(X)
# 残差分布检验
residuals = Y - Y_pred
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.hist(residuals, bins=20)
plt.title('Residuals Histogram')
plt.xlabel('Residuals')
plt.ylabel('Frequency')
plt.subplot(1, 2, 2)
plt.scatter(Y_pred, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.title('Residuals vs Predictions')
plt.xlabel('Predictions')
plt.ylabel('Residuals')
plt.show()
# 计算均方误差
mse = mean_squared_error(Y, Y_pred)
print("Mean Squared Error:", mse)
# Mean Squared Error: 0.9924386487246479
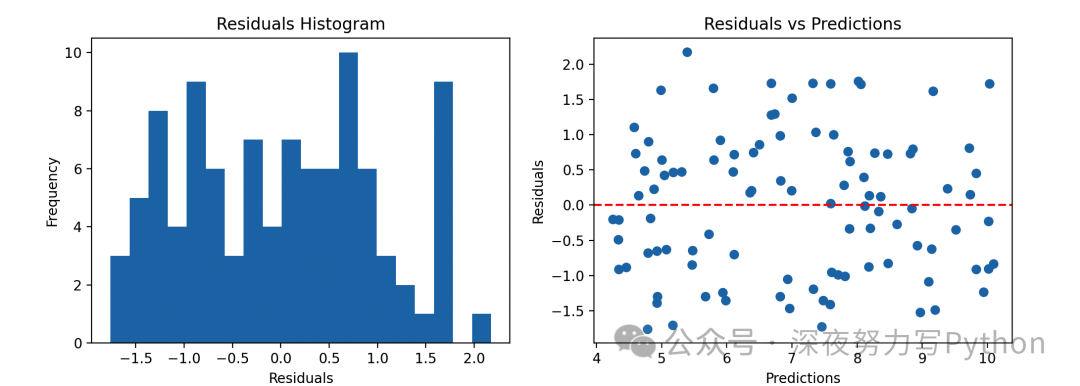
使用线性回归模型对数据进行拟合。绘制了残差的直方图和残差与预测值的散点图,并计算了模型的均方误差。
通过观察直方图和散点图,可以初步判断残差是否近似于正态分布、是否存在异方差性。根据均方误差的大小,可以评估模型的拟合程度。
8. 预测与推断
预测与推断能够利用模型对未知数据进行预测,并对自变量与因变量之间的关系进行推断。
- 预测(Prediction): 在线性回归中,预测是指利用已训练的模型对未知数据进行输出值的估计。通过模型的预测,可以根据自变量的特征来预测因变量的值。这对于解决实际问题中的预测任务非常重要,比如房价预测、销售预测等。
- 推断(Inference): 推断是指利用已训练的模型来了解自变量与因变量之间的关系,以及各个自变量对因变量的影响程度。通过推断,可以回答一些问题,比如哪些自变量对因变量有显著影响、这些影响的方向是正向还是负向、以及它们的影响程度如何等。
假设有一个简单的数据集,包含一个自变量
和一个因变量
。
使用线性回归模型拟合这个数据集,然后进行预测和推断。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成样本数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
Y = 4 + 3 * X + np.random.randn(100, 1) # 加入随机噪声
# 拟合线性回归模型
model = LinearRegression()
model.fit(X, Y)
# 进行预测
new_X = np.array([[1.5]]) # 新的自变量值
predicted_Y = model.predict(new_X)
print("Predicted Y for new X:", predicted_Y[0][0])
# 进行推断
print("Intercept (β₀):", model.intercept_[0])
print("Coefficient (β₁):", model.coef_[0][0])
# Predicted Y for new X: 8.67485234349876
# Intercept (β₀): 4.222151077447231
# Coefficient (β₁): 2.968467510701019
代码中,给定一个新的自变量值
,可以利用模型预测对应的因变量值
。
然后,进行推断,通过模型的截距和系数来了解自变量
对因变量
的影响。在这个例子中,截距
表示当自变量
为0时,因变量
的预测值;系数
表示自变量
每增加1单位时,因变量
的变化量。这是推断的应用方面。
通过预测和推断,咱们可以充分利用线性回归模型来理解数据集的特征,进行未知数据的预测,并推断自变量与因变量之间的关系。