【图论】图论基础（搜索、最短路、并查集、最小生成树、拓扑排序）

Karos

修改于 2023-02-01 11:28:16

7770

修改于 2023-02-01 11:28:16

文章被收录于专栏：MyBlog-Karos MyBlog-KarosMyBlog-Karos

提示代码仅提供引发思路作用，部分地方代码可能又不足之处，也希望有大佬能够补充

图

基本概念

图论(Graph Theory)是离散数学的一个分支，是一门研究图(Graph)的学问。

图是用来对对象之间的成对关系建模的数学结构，由”节点”或”顶点”(Vertex）以及连接这些顶点的”边”（Edge）组成。

值得注意的是，图的顶点集合不能为空，但边的集合可以为空。图可能是无向的，这意味着图中的边在连接顶点时无需区分方向。否则，称图是有向的。下面左图是一个典型的无向图结构，右图则属于有向图。本章节介绍的图都是无向图。

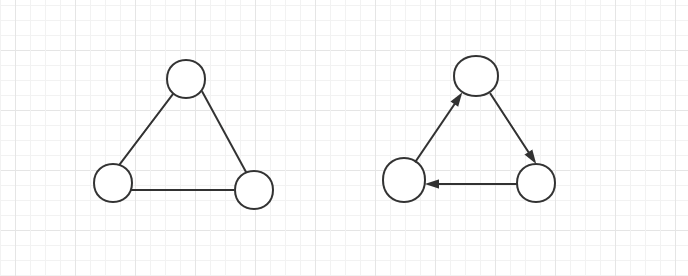
图的分类：无权图和有权图，连接节点与节点的边是否有数值与之对应，有的话就是有权图，否则就是无权图。

图的连通性：在图论中，连通图基于连通的概念。在一个无向图 G 中，若从顶点 i 到顶点 j 有路径相连（当然从j到i也一定有路径），则称 i 和 j 是连通的。如果 G 是有向图，那么连接i和j的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图（注意：需要双向都有路径）。图的连通性是图的基本性质。

完全图：完全是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。

自环边：一条边的起点终点是一个点。

平行边：两个顶点之间存在多条边相连接。

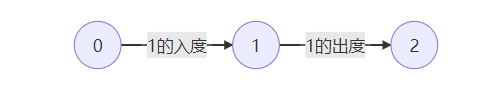
入度：指向某一个点

出度：某个点指出

图的表示 — 存图

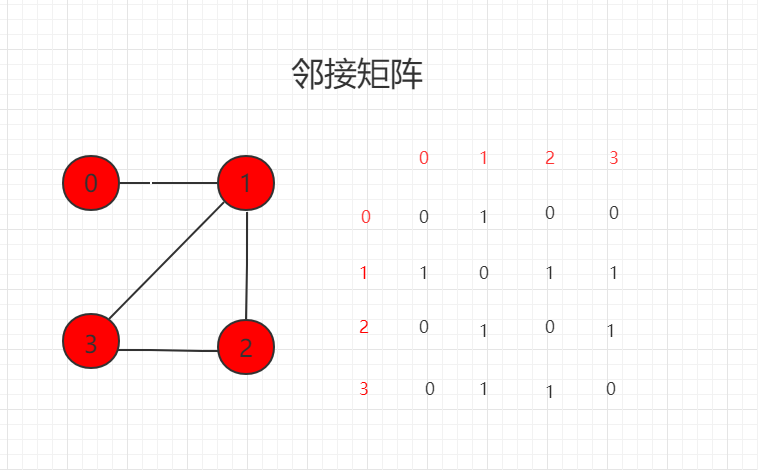
邻接矩阵

1 表示相连接，0 表示不相连。

#include <iostream>
#include INF 0x3f3f3f
using namespace std;
int a[505][505];
int main(){
    memset(a,0,sizeof(a));//无权图，初始化为0
    int n,m;//n个点 m条边
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int u,v;//u 起点 v 终点
        cin>>u>>v;
        a[u][v]=a[v][u]=1;//无向图
    }
}

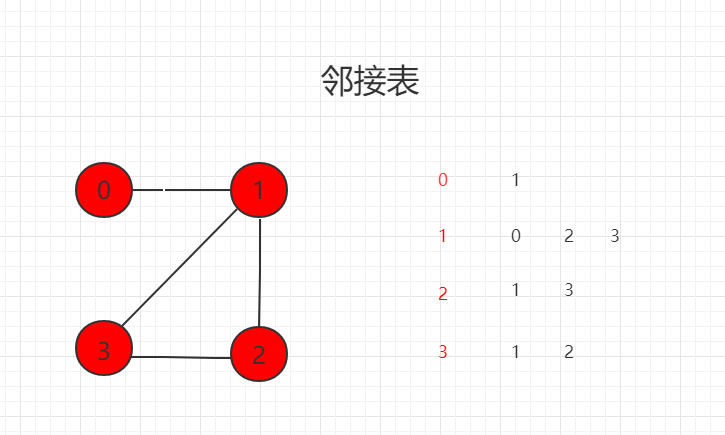
邻接表（进阶，初学请先熟练邻接矩阵）

只表达和顶点相连接的顶点信息

#include <iostream>
#include <vector>
using namespace std;

vector<vector<int> >e;

int main(){
    int n,m;//n个点 m条边
    cin>>n>>m;
    //初始化e
    //有n个点，第一维为n，如果起点为1，那就循环n+1次
    for(int i=0;i<n;i++){
        vector<int> temp;
        e.push_back(temp);
    }
    for(int i=0;i<m;i++){
        int u,v;
        cin>>u>>v;
        e[u].push_back(v);
        e[v].push_back(v);
    }
}

边集数组

#include <bits/stdc++.h>;
using namespace std;
typedef struct edge{
    int u,v,w;
}edge;
int main(){
    int n,m;
    cin>>n??m;
    edge e[m];
//边集数组存储方式
    for (int i = 0; i &lt; m; ++i) {
        int u,v,w;
        cin&>>u>>v>>w;
        e[i]={u,v,w};
    }
}

链式前向星（进阶后再看）

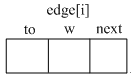
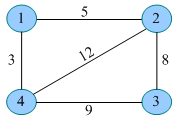
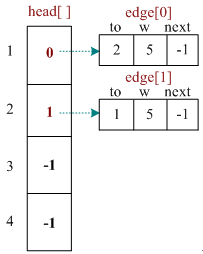
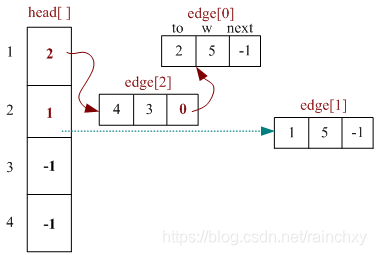
typedef struct edge{
    int to;//终点
    int w;//权重
    int next;//兄弟结点在e数组中的下标
}edge;
//这里使用动态数组，使用普通数组也是可以的
vector<edge>e;
vector<int>head;//建议从1开始存，其值是指向一个e的下标

//后面可以用vector练习一下
#include <iostream>
#include <string.h>
using namespace std;
typedef struct edge{
    int to;//终点
    //权值，存图不记录权值可以不用
  //  int w;
    int next;//下一条边的下标
}e[100001];
e edg;
int head[10001],_pos;
int main(){
    memset(head,-1,sizeof(head));//head的下标代表起点，存储的是 起点到终点 那条边在edg中的下标
    int n,m;//n个点 m条边
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int u,v;
        cin>>u>>v;
        //下面两句话我们一般写成一个函数
        e[_pos]={v,head[u]};//e[_pos]={v,w,head[u]};
        head[u]=_pos++;
    }
}

图的遍历（假设你已经存好图）

深度优先搜索

邻接矩阵

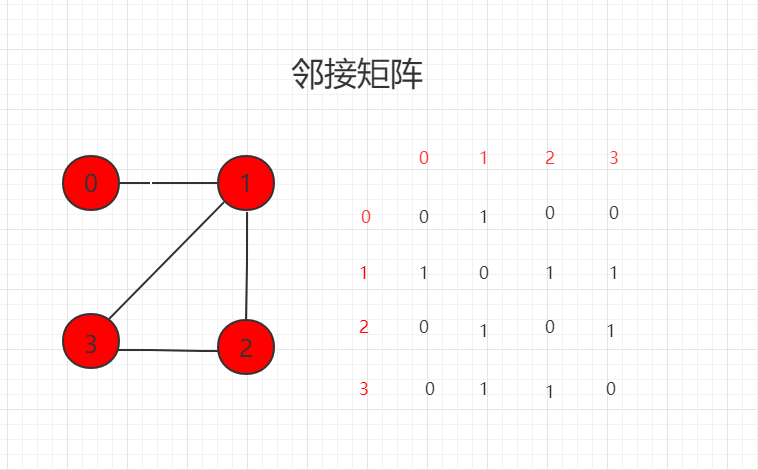
0->1->2->3（按照顺序）

//我们注意一下
//这里我们得分几种情况
//   当走到某一个点后，这个点我们走没走过？
//   这个点能不能走？
//这两个问题
//对于第一个问题：用一个数组 book来标记，如果走过，就回到上一步，避免重复走环（死循环）
//第二个，更简单了直接判断数组 !a[i][j] 那就不走
//

int book[n];//标记这个点有没有走过
void dfs(int pos){
//    if(book[pos]) return ;//如果这个点走过，则返回
    cout<<pos<<endl;
    book[pos]=true; //这道题就不用回溯了
    for(int i=0;i<n;i++){
        if(!book[i]&&a[pos][i]){
            dfs(i);
        }
    }
}

邻接表

int book[n];//标记这个点有没有走过
vector<vector<int> >edge;
void dfs(int pos){
//    if(book[pos]) return ;//如果这个点走过，则返回
    cout<<pos<<endl;
 book[pos]=true; //这道题就不用回溯了
    for(int i=0;i<a[pos].size();i++){
        if(!book[a[pos][i]]){
            dfs(a[pos][i]);
        }
    }
}

链式前向星

typedef struct Edge{
    int to;
    int w;
    int next;
}Edge;
Edge e[10000];
int head[10000];
bool book[10000];
void dfs(int pos){
 //   if(book[pos])return ;
    cout<<pos<<endl;
    book[pos]=true;
    for(int i=head[pos];i+1;i=e[i].next){
        int v=e[i].to;
        if(!book[v]){
            dfs(v);
        }
    }
}

广度优先搜索

邻接矩阵

#include <iostream>
#include <queue>
#define INF 0x3f3f3f
using namespace std;
int n,m;
int a[1000][1000];
bool book[1000];
void init(){
    memset(a,INF,sizeof(INF));
    for(int i=0;i<=n;i++)a[i]=0;
}
queue<int>que;
void bfs(int pos){
    cout<<pos<<" ";
    que.push(pos);
    book[pos]=true;
    while(!que.empty()){
        int u=que.front();
        cout<<u;
        for(int i=1;i<=n;i++){
            if(!book[i]&&a[u][i]==1){
                que.push(i);
                book[i]=true;
            }
        }
        que.pop();
    }
}
int main(){
    init();
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int u,v;
        a[u][v]=a[v][u]=1;
    }
    bfs(1);
}

邻接表

自己试着写写

链式前向星

自己试着写写

稠密图与稀疏图

一个图中，顶点数 n 边数 m

当n^2>>m 时，我们称之为稀疏。(点多边少)

当m相对较大时，我们称之为稠密。(点和边差不多)

最短路径算法

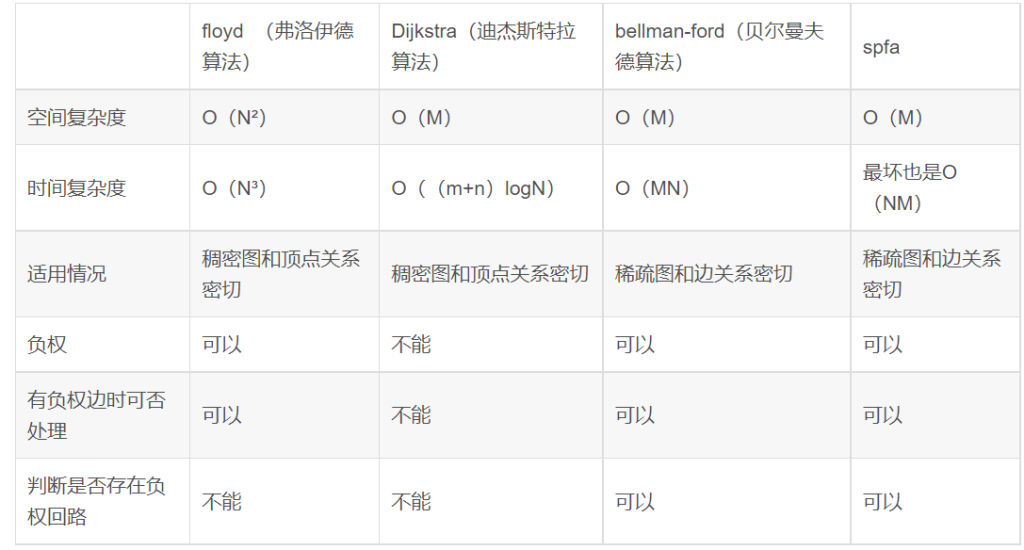
Floyd – 多源最短路

三个for循环，找个中间点，松弛（更新最短路）每一个点

for(int k=0;k<n;k++)
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            if(a[i][j]>a[i][k]+a[k][j])
                a[i][j]=a[i][k]+a[k][j];

优点：三个for完了以后可以取出任意两点之间的最短路径可以有负权

缺点：时间复杂度很大

适用情况：稠密图且数据量不是很大的时候

思想：dp算法（动态规划）

Dijkstra – 迪杰斯特拉单源最短路

Dijkstra算法（后面简称dj算法），基本思想是贪心。

比如我们要找到1到各个点的最短路径，那我们不妨把一设为源点

我们每次通过找离源点最近的其他点（贪心思想）来松弛（专业术语，你可以理解为更新）源点到其他点的最短路径。

比如像下面这个图

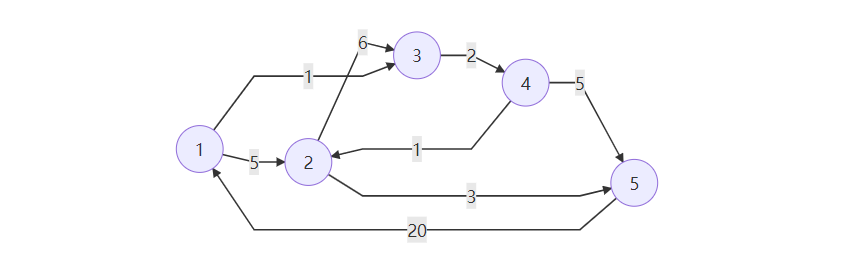
在此之前，我们定义一个数组dis，把1到每个点的距离存进去

i	1	2	3	4	5
dis[i]	0	5	1	INF	INF

我们先找离1最近的点，是3

通过3来松弛1->4的距离松弛以后

dis[4]=min(dis[4],dis[3]+a[3][4])=3

i	1	2	3	4	5
dis[i]	0	5	1	3	INF

这个时候我们继续找离1最近的点，这个时候3已经找过了，只有4

我们通过dis[4]进行松弛（原则上到不了的点以及距离本来就较短的点也会算入松弛，我就不写了）

dis[2]=min(dis[2],dis[4]+a[4][2])=4

dis[5]=min(dis[5],dis[2]+a[4][5])=8

这一轮松弛完了，继续

i	1	2	3	4	5
dis[i]	0	4	1	3	8

那接下来，就靠2来松弛

dis[3]=min(dis[3],dis[2]+a[2][3])=1

dis[4]=min(dis[4],dis[2]+a[2][4])=3

dis[5]=min(dis[5],dis[2]+a[2][5])=7

i	1	2	3	4	5
dis[i]	0	4	1	3	7

我们可以发现，有n个点，那我们就要进行n-1轮松弛

下面是代码：

邻接矩阵

#include <iostream>
#include <cstring>
#define INF 0x3f3f3f
using namespace std;
int a[500][500],dis[500];
bool book[500];//标记某个点是否松弛过
int main(){
    //初始化所有点为无穷，到得了的点就录入，到不了就默认为INF（无穷大）
    memset(a,INF,sizeof(a));//注意：sizeof不可对数组指针（指向数组的指针）使用
    memset(dis,INF,sizeof(dis));
    for(int i=0;i<=500;i++) a[i][i]=0;//自己到自己的距离为零
    int n,m;
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int u,v,w;
        cin>>u>>v>>w；
        a[u][v]=w;//有向图
    }
    //初始化dis数组，记录源点到其他点的初始距离,这里源点是1
    for(int i=0;i<n;i++)
        dis[i]=a[1][i];//源点为s -> dis[i]=a[s][i];
    book[1]=true;
    //松弛n-1次
    for(int i=0;i<n-1;i++){
        int u;//找离源点最近的且没有被访问过的点
        int min=0x3f3f3f;
        //如果有0的话从0开始
        for(int j=1;j<=n;j++){
            if(!book[j]&&dis[j]<min){
                min=dis[j];
                u=j;
            }
        }
        book[u]=true;
        //如果有0的话从0开始
        for(int j=1;j<=n;j++){
            if(!book[j]&&dis[j]>dis[u]+a[u][j])//a[u][j]<INF
                dis[j]=dis[u]+a[u][j];
        }
    }
    cout<<dis[n];
}

邻接表

#include <iostream>
#define _to int
#define _value int
#define INF 0x3f3f3f
using namespace std;
vector<vector<pair<_to,_value> >e;//pair第一个是终点，第二个是权值
bool *book[100000];
int n,m;//点数 边数
//初始化函数
void init(){
    for(int i=0;i<=n;i++){
        vector<int>　p;
        e.push_back(p);
    }
    memset(dis,INF,sizeof(int))
}
//加边函数
void add(int u,int v,int w){
    e[u].push_back(make_pair(v,w));
}
int main(){
    cin>>n>>m;
    init();
    for(int i=0;i<m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
        //add(v,u,w); 无向图加上
        if(u==1)      dis[v]=w; 
    }
    dis[1]=0;
    book[1]=true;
    for(int i=0;i<n-1;i++){
        int u,min=INF;
        for(int j=1;j<=n;j++){
            if(!book[j]&&dis[j]<min){
                min=dis[j];
                u=j;
            }
              book[u]=true;
       
        for(int j=0;j<e[u].size;j++){
            int p=e[u][j].first;
            if(!book[p]&&dis[p]>dis[u]+e[u][j].second)
                dis[p]=dis[u]+e[u][j].second;
        }
    }
        cout<<dis[n];
}

前向星

#include <iostream>
#include <string.h>
#define INF 0x3f3f3f
using namespace std;
typedef struct edge{
    int to,w,next;
}edge;
int head[10000];
edge e[100000];
int _size;//当前边数
int dis[100000];
void add(int u,v,w){
    e[_size]={v,w,head[u]};
    head[u]=_size++;
}
void init(){
    memset(head,-1,sizeof(head));
}
int main(){
   int n,m;
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
        //add(v,u,w); 无向图加上
        if(u==1)      dis[v]=w;
    }
    dis[1]=0;
    book[1]=true;
    for(int i=0;i<n-1;i++){
        int u,min=INF;
        for(int j=1;j<=n;j++){
            if(!book[j]&&dis[j]<min){
                min=dis[j];
                u=j;
            }
              book[u]=true;
       
        for(int j=head[u];j+1;j=e[j].next){
            int p=e[j].to;
            if(!book[p]&&dis[p]>dis[u]+e[j].w)
                dis[p]=dis[u]+e[j].w;
        }
    }
        cout<<dis[n];
}

堆优化的dj

堆优化也就是在找离源点最近的点的时候采用最小堆

#include <iostream>
#include <string.h>
#include <set>
#define INF 0x3f3f3f
using namespace std;
set<pair<int ,int> ,less<pair<int,int> > >s;//第一个为权值，第二个为点的下标
typedef struct edge{
    int to,w,next;
}edge;
int head[10000];
edge e[100000];
int _size;//当前边数
int dis[100000];
bool book[100000];
void add(int u,int v,int w){
    e[_size]={v,w,head[u]};
    head[u]=_size++;
}
void init(){
    memset(head,-1,sizeof(head));
}
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
        //add(v,u,w); 无向图加上
        //if(u==1)      dis[v]=w; 我们不需要初始化，后面会通过源点更新
    }
    dis[1]=0;
    book[1]=true;
    s.insert(make_pair(0,1));
    int flag = 0 ;
    for(int i=0;i<n-1;i++){
        if(s.empty()){
            flag=1;//有点到不了，可以判断是否又独立店
            break;
        }
        int u=s.begin()->second;
        book[u]=true;
        s.erase(*s.begin());//把当前最近的点删除，避免二次松弛
        for(int j=head[u];j+1;j=e[j].next){
            int p=e[j].to;
            if(!book[p]&&dis[p]>dis[u]+e[j].w){
                s.erase(make_pair(dis[p],p));
                dis[p]=dis[u]+e[j].w;
                s.insert(make_pair(dis[p],p));
            }
        }
    }
    cout<<dis[n];
}

测试题史东薇尔城

J-史东薇尔城_2022年中国高校计算机大赛-团队程序设计天梯赛（GPLT）上海理工大学校内选拔赛 (nowcoder.com)

AC代码：

#include <iostream>
#include <set>
#include <string.h>
#define INF 999999999999999
#define pii pair<long long,long long>
using namespace std;
long long n,m;
typedef struct edge{
    long long to,w,next;
}Edge[400005];
Edge e;
long long _size=0;
long long head[400005];
void add(long long u,long long v,long long w){
    e[_size]={v,w,head[u]};
    head[u]=_size++;
}
long long dis[400005];
bool book[400005];
set<pii>s;
void dj(long long pos){
    dis[pos]=0;
    book[pos]=true;
    s.insert({0,pos});
    for(long long i=0;i<n-1;i++){
        if(s.empty()){break;}
        long long u=s.begin()->second;
        book[u]=true;
        s.erase(*s.begin());
        for(long long j=head[u];j+1;j=e[j].next){
            long long v=e[j].to;
            if(!book[v]&&dis[v]>dis[u]+e[j].w){
                s.erase({dis[v],v});
                dis[v]=dis[u]+e[j].w;
                s.insert({dis[v],v});
            }
        }
    }
}
int main(){
    cin>>n>>m;
    fill(dis,dis+200005,INF);
    memset(book,false,sizeof(book));
    memset(head,-1,sizeof(head));
    for(long long i=0;i<m;i++){
        long long u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
        add(v,u,w);
    }
    dj(1);
    long long T;
    cin>>T;
    while(T--){
        long long u,v;
        cin>>u>>v;
        printf("%lld\n",dis[u]+dis[v]);
    }
}

Bell-Man Ford -贝尔曼福特单源最短路

贝尔曼福特算法使用边集数组，通过边集数组直接找

#include <iostream>
#define INF 0x3f3f3f
using namespace std;
typedef struct edge{
    int u,v,w;
}edge;
edge e[10000];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        e[i]={u,v,w};
    }
    for(int i=0;i<n-1;i++)
        for(int j=0;j<=m;j++){
          //   if(dis[e[j].u]>=INF) continue;
            if(dis[e[j].v]>dis[e[j].u]+e[j].w)
                dis[e[j].v]=dis[e[j].u]+e[j].w
        }
    int flag=0;
    for(int j=0;j<=m;j++){
        if(dis[e[j].v]>dis[e[j].u]+e[j].w){
                flag=1;
            }  
       }
    cout<<dis[n-1];
    if(flag)cout<<"有负环";
}

SPFA – 贝尔曼福特算法队列优化

SPFA算法 – SHHHS – 博客园 (cnblogs.com)

源点->找邻点->入队->松弛并记录

#include <iostream>
#include <cstring>
#include <queue>
#define INF 0x3f3f3f
using namespace std;
typedef struct edge{
    int to,w,next;
}edge;
int _size;
int head[10001];
int dis[10001];//记录距离
int cnt[10001];//记录入队次数
bool book[10001];//判断是否入队
edge e[10001];
queue<int> que;
void add(int u,int v,int w){
    e[_size]={v,w,head[u]};
    head[u]=_size++;
}
void init(){
   memset(head,-1,sizeof(head));
   memset(dis,INF,sizeof(dis));
}
int main(){
    init();
    int flag=0;
    int n,m;
    cin>>n>>m;
    for(int i=0;i<m;i++){
     int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
    }
    dis[1]=0;//源点 1
    book[1]=true;
    que.push(1);
    while(!q.empty()){
        int u=q.front();
        q.pop();
        book[q]=false;
        for(int j=head[u];j+1;j=e[j].next){
            int v=e[j].to;
            if(dis[v]>dis[u]+e[j].w){
                dis[v]=dis[u]+e[j].w;
                if(!book[v]){
                    que.push(v);
                    book[v]=true;
                    if(++cnt[v]>n-1){
                        flag=1;
                        break;
                    }
                }
            }
        }
        if(flag) break;
    }
    cout<<dis[n-1]<<endl;
    if(flag) cout<<"有负环存在";
}

并查集

把很多个具有相同特点的元素，合并成一个集合来考虑

把 1和2 合并（按照右归左的规定）

如果在这个时候，我们要把3和2合并，那这个时候2到底是属于1还是属于3，但明显我们要两个都属于

那么我们可以把3和1合并

也就是把祖宗指向新进来的元素

试想一下，把2和4合并和把4和2合并又该怎么做？

方法：

①初始化

②找祖宗

③合并

先说说初始化，我们先定义一个普通的一维数组a[n]，并且使得a[i]=i

int a[100];
void init(){
    for(int i=0;i<100;i++) a[i]=i;
}

找祖宗的算法怎么写？

我们定义一个函数，如果说一个数a[i]是祖宗，那么他的值一定是i

像上面的图

a[i]	1	2	3	4
i	3	3	3	4

这是经过了合并以后的，那现在来看看找祖宗函数该怎么写

int find(int x){
    //如果找到祖宗，则返回祖宗编号
    if(a[x]==x) return x;
    //否则 继续向上找，并把每个中间结点的父亲都变成祖宗
    return a[x]=find(a[x]);
}

那合并怎么写？

看代码

bool merrge(int x,int y){
    //如果两个数本就是一个集合，那就直接return；
  int _posx=find(x);
    int _posy=find(y);
    if(_posx==_posy) return false;//没有进行合并或者说之前已经合并过，返回false
    //思考：为何不直接if(a[x]==a[y]) return;
    a[_posx]=_posy;
    return true;
}

当全部合并完成后有什么用？

看有几个团体，如果合并后a[i]==i，那算一个

下面来讲讲并查集的用法之一

图的最小生成树（Kruskal算法）

生成树（spanning tree） ：一个连通无向图的生成子图，同时要求是树。也即在图的边集中选择n-1条，将所有顶点连通。

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

我们可以通过排序，或者用堆，每次取出权值最小的来加上。

这里，我们采取边集数组存储

#include <iostream>
using namespace std;
typedef struct edge{
    int u,v,w;//起点 终点 权值
    const bool operator <(const edge b){
        return this->w<b.w;
    }
}edge;
int a[100];
void init(){
    for(int i=0;i<100;i++) a[i]=i;
}
int find(int x){
    //如果找到祖宗，则返回祖宗编号
    if(a[x]==x) return x;
    //否则 继续向上找，并把每个中间结点的父亲都变成祖宗
    return a[x]=find(a[x]);
}
bool merrge(int x,int y){
    //如果两个数本就是一个集合，那就直接return；
 int _posx=find(x);
    int _posy=find(y);
    if(_posx==_posy) return false;//没有进行合并或者说之前已经合并过，返回false
    //思考：为何不直接if(a[x]==[y]) return;
    a[_posx]=_posy;
    return true;
}
int main(){
    int n,m;//n个点 m条边
    cin>>n>>m;
    edge e[m];
    for(int i=0;i<m;i++){
        int u,v,w;
        cin>>u>>v>>w;
        e[i]={u,v,w};
    }
    sort(e,e+m);
    int dis=0;
    int cnt=0;
    for(int i=0;i<m;i++){
        //如果是一条通路，且没有换，那么每个点应该属于同一个集合
        if(merrge(e[i].u,e[i.v])){
            dis+=e[i].w;
            if(++cnt==n)break;
        }
    }
    cout<<dis;
}

拓扑排序

在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

每个顶点出现且只出现一次。若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

算法导论上这样说：对于一个有向无环图 G= (V,E) 来说，其拓扑排序是中所有结点的一种线性次序，该次序满足如下条件：如果图含边 (u, v), 则结点在拓扑排序中处于结点的前面（如果图包含环路，则不可能排出一个线性次序）。可以将图的拓扑排序看做是将图的所有结点在一条水平线上排开，图的所有有向边都从左指向右。因此，拓扑排序与本书第二部分所讨论的通常意义上的＂排序”是不同的。

先说一下拓扑排序的步骤：

将所有入度为0的点入队
从图中删除该顶点和以该顶点为起点的边
去掉后如果入读为0则入队

#include <iostream>
#include <queue>
#include <string.h>
using namespace std;
typedef struct edge{
    int to,next;
}Edge[10000];
Edge e;
int _size;
int head[10000];
int inq[10000];//记录入度
queue<int> que;
void add(int u,int v){
    e[_size]={v,head[u]};
    head[u]=_size++;
}
int main(){
    int n,m;
    cin>>n>>m;
    memset(head,-1,sizeof(head));
    for(int i=0;i<m;i++){
        int u,v;
        //孤点 v=0
        cin>>u>>v;
 if(v){
       add(u,v);
      inq[v]++;
   }       
        
    }
    //将所有入度为0的点入队
      for(int i=1;i<=n;i++)
        if(!inq[i])que.push(i);
    while(!que.empty()){
        int u=que.front();
        que.pop();
     cout<<u<<" ";
        for(int j=head[u];j+1;j=e[j].next){
            int v=e[j].to;
            cout<<v<<" ";
            inq[v]--;
            if(!inq[v])que.push(v);
        }
        cout<<endl;
    }
}

参考文献：https://blog.csdn.net/lisonglisonglisong/article/details/45543451

《算法导论 – 原书第3版译》

本文参与腾讯云自媒体分享计划，分享自作者个人站点/博客。

原始发表：2022-5-06 1，如有侵权请联系 cloudcommunity@tencent.com 删除

数据结构

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体分享计划，欢迎热爱写作的你一起参与！

数据结构

#算法

#图论

登录后参与评论

0 条评论

热度