【图论】简单概念及公式入门 ( 完全图 | 二部图 | 连通图 | 欧拉回路 | 哈密顿圈 | 平面图 | 欧拉定理 )

韩曙亮

发布于 2023-03-27 16:31:08

1.4K0

发布于 2023-03-27 16:31:08

文章被收录于专栏：韩曙亮的移动开发专栏

文章目录

一、完全图

完全图概念 :

1.条件 1 :

为

n (n \geq 1)

阶无向简单图 ;

2.条件 2 : 若

中每个顶点均与其余的

n-1

个顶点相邻 ;

3.结论 : 则称

为

阶无向完全图 , 记做

K_n

;

的顶点集是

V(G)

, 其顶点个数为

|V(G)|

, 则称

为

阶图 ;

二、二部图

二部图概念 :

1.条件 1 : 图

的顶点集划分为两个非空子集

和

;

2.条件 2 : 一条边有一个端点在

中 , 另一个端点在

中 ;

3.结论 : 满足上述条件 , 称

是二部图或偶图 ;

4.标记 : 记做

G=(X \cup Y , E)

(X, Y)

是

的一个划分 ( 二分类 ) ;

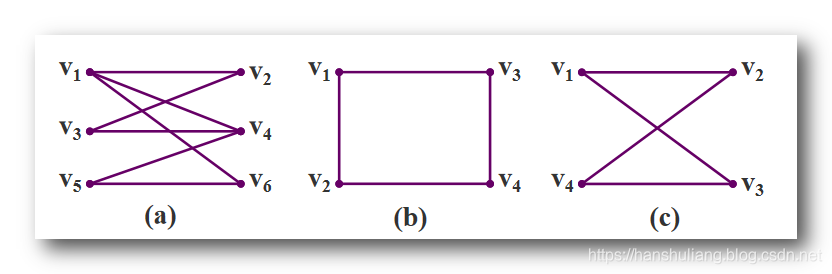
其中

( a )

是二部图 ,

( b )

也是二部图 , 其不明显 , 改变

( b )

中顶点和边位置 , 可以得到

( c )

, 此时就能看出其是二部图 ;

注意 : 二部图的一边中不允许有边相连 ;

指的是 Graphic 图 ;

指的是 Edge 边 ;

指的是 Vertext 顶点 ;

三、完全二部图

完全二部图概念 :

1.条件 1 : 简单二部图

G=(X \cup Y, E)

2.条件 2 : 如果

中的每个顶点与

中的每个顶点都有边连接 ;

3.结论 : 满足上述条件的二部图

, 称为完全二部图 ;

4.记法 :

|X|=m

|Y|=n

, 此完全二部图记做

K_{m,n}

;

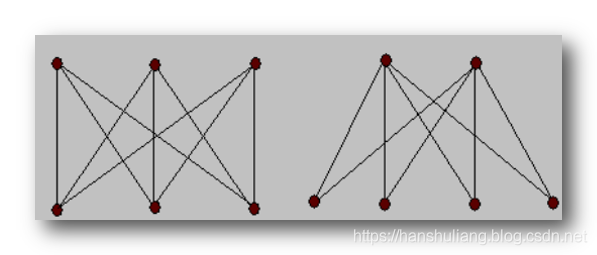
5.特殊存在 :

K_{1,n}

称为星 ;

指的是 Graphic 图 ;

指的是 Edge 边 ;

指的是 Vertext 顶点 ;

四、连通性概念

图中两个顶点的连通 :

条件

: 如果在图

中 , 存在两个顶点

u,v

;

条件

: 两个顶点之间存在

(u,v)

路 ;

结论 : 满足上述条件 , 则称 点

u,v

在图

中连通 ;

涉及到的其它概念 : 途径 : 顶点和边的交替出现的序列 , 其顺序符合图中的位置即可 ; 迹 : 每个边不能相同的 途径 ; 路 : 每个点都不相同的 迹 ; 这三个概念 , 一个比一个严格 ; 闭途径 : 起点和终点相同的 途径 ; 闭迹 : 起点和终点相同的 迹 , 也称回路 ; 圈 : 起点和终点相同的 路 ;

指的是 Graphic 图 ;

指的是 Edge 边 ;

指的是 Vertext 顶点 ;

五、连通图

连通图 : 图

中 , 任意两个顶点都连通 , 那么这个图

是连通图 ;

六、图的分支

图的分支 :

条件 1 : 图

顶点集

V(G)

划分为若干非空子集

\{V_1, V_2, \cdots , V_n\}

;

条件 2 : 两个顶点属于同一个子集 , 当且仅当它们在

中连通 ;

满足上述条件 : 称每个子图

G[V_i]

是图

的一个分支 ;

( i=1,2,3,\cdots,n )

指的是 Graphic 图 ;

指的是 Edge 边 ;

指的是 Vertext 顶点 ;

七、欧拉回路 ( 闭迹 / 回路 ) [ 遍历图中所有的边 | 每个边只经过一次 | 顶点可经过多次 ]

欧拉回路 : 图

G(V,E)

中所有边的回路 ( 闭迹 ) 称为 欧拉回路 ;

涉及到的其它概念 : … 途径 : 顶点和边的交替出现的序列 , 其顺序符合图中的位置即可 ; 迹 : 每个边不能相同的 途径 ; 路 : 每个点都不相同的 迹 ; … 这三个概念 , 一个比一个严格 ; … 闭途径 : 起点和终点相同的 途径 ; 闭迹 : 起点和终点相同的 迹 , 也称回路 ; 圈 : 起点和终点相同的 路 ; …

指的是 Graphic 图 ;

指的是 Edge 边 ;

指的是 Vertext 顶点 ;

八、欧拉定理

欧拉定理 :

无向图存在欧拉回路的充要条件 :

① 图是连通的 ;

② 图中没有度数是奇数的顶点 ;

与顶点

关联的边数之和 ( 环算

条边 ) 就是该顶点的度 , 记作

d(v)

九、哈密顿圈 ( 闭路 / 圈 ) [ 遍历图中所有的顶点 | 每个顶点只经过一次 ]

图

G=(V,E)

中 , 从某顶点出发 , 将所有顶点遍历一遍 , 每个顶点只经过一次 ;

G=(V,E)

中经过

中所有顶点的圈 , 称为哈密顿圈 ;

G=(V, E)

中经过

中所有顶点的道路 , 称为哈密顿道路 ;

涉及到的其它概念 : … 途径 : 顶点和边的交替出现的序列 , 其顺序符合图中的位置即可 ; 迹 : 每个边不能相同的 途径 ; 路 : 每个点都不相同的 迹 ; … 这三个概念 , 一个比一个严格 ; … 闭途径 : 起点和终点相同的 途径 ; 闭迹 : 起点和终点相同的 迹 , 也称回路 ; 圈 : 起点和终点相同的 路 ; …

指的是 Graphic 图 ;

指的是 Edge 边 ;

指的是 Vertext 顶点 ;

十、哈密顿圈相关定理

定理 :

设

G(V,E)

是

n (n\geq 2)

个顶点的简单图 , 如果任意一对顶点的度数之和 大于等于与

n-1

, 则

中一定有哈密顿道路 ;

推论 :

设

G(V,E)

是

n (n\geq 3)

个顶点的简单图 , 如果任意一对顶点的度数之和 大于等于与

, 则

中一定有哈密顿道路 ;

注意这里是任意一对顶点的度数之和大于等于

n(n\geq3)

, 所有的能找出来的顶点都要满足该条件 ;

十一、平面图

平面图定义 :

1.条件 :

G=<V,E>

是一个无向图 ;

2.行为 : 将

的所有的节点和边画在平面上 , 使任何两条边除了端点外没有其他的交点 ;

3.结论 : 满足上述要求 ,

是平面图 ;

平面图的特殊情况 , 改变边的形状可以使相交的边不相交 , 这个图是平面图 ;

有些图表面上看 , 有相交的边 , 但是不能肯定其不是平面图 , 改变某些边的形状 , 可以使各个边不相交 , 那这个图还是平面图 ; 如下图 , 左图有相交的边 , 但是把边拉出来到外侧 , 各个边可以不相交 , 因此该图是平面图 ;

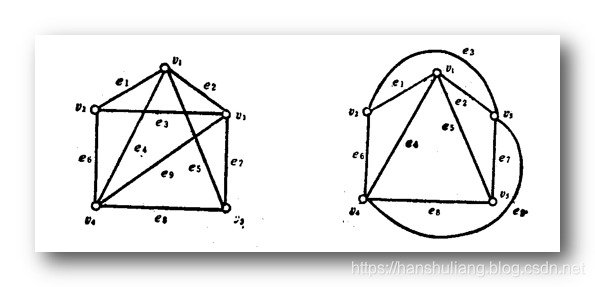
有些图其边相交 , 但是无论怎么改变其顶点位置和边的形状 , 总是有相交的边 , 那么这个图不是平面图 ;

十二、面的次数与边数定理 ( 面次数之和 = 边数两倍 ) ★

设

是有限平面图 , 面的次数之和 等于边数 的两倍 ;

有限平面图中 , 边在平面中划分的区域成为面 , 包围每个面的边的个数成为面的次数 , 又称为面的度数 ;

有限区域 : 有限面 , 三角形内部的面
无线区域 : 无限面 , 三角形外部的面

十三、欧拉定理 ★

是平面连通图 ,

是顶点数 ,

是边数 ,

是面数 ;

欧拉公式 :

v - e + r = 2

( 该公式是顶点边面之间的关系 , 没有面的度数 )

面的度数之和是

, 可以与上面组成方程组 , 前提是

是平面连通图 ;

: 顶点数 ;

: 边数 ;

: 面数 ;

d_{all}

: 所有面度数之和 ; 公式 1 :

2e = d_{all}

, 设

是有限平面图 , 面的次数之和 等于边数 的两倍 公式 2 :

v -e + r = 2

公式 3 :

是平面图

\Rightarrow

e \leq 3v - 6

助记 : 三角形 : 3 个顶点 , 3条边 , 2个面 ( 内部一个面 , 外部一个面 )

十四、平面图的必要条件定理 ( 平面图满足 e 小于等于 3v -6 条件 ) ★

是简单连通平面图 , 其顶点数

v\geq3

, 其边数

;

那么

e \leq 3v - 6

;

如果是平面图 , 那么公式一定成立 ; 公式成立 , 这个图不一定是平面图 ;

该定义用来证明该图不是平面图 , 公式不成立 , 那么该图一定不是平面图 ;

十五、图的模型应用★

题目 :

条件

: 一个班级的学生选修

A,B,C,D,E,F

六门课程 ;

条件

: 一部分人同时选修

D,C,A

, 一部分人同时选修

B,C,F

, 一部分人选修

B,E

, 还有一部分人选修

A,B

问题 : 要求安排考试 , 不能有学生连续两天参加考试 ;

解题思路 :

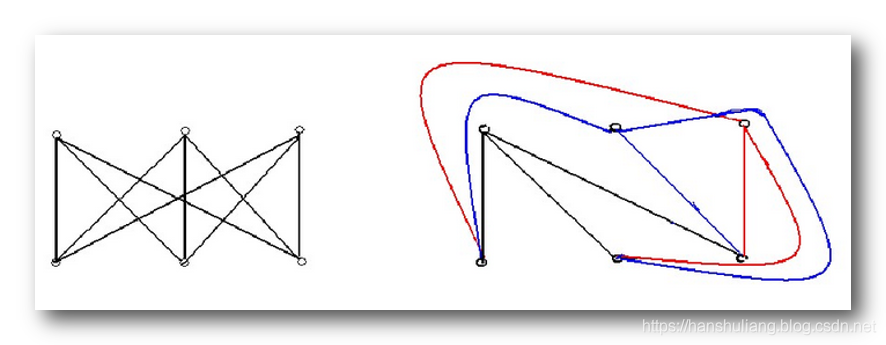
1.构造图 : 每门课程当做一个顶点 , 共同被选修的课程用边相连 ;
2.构造补图 : 将其它顶点用虚线连起来 , 虚线部分是上图的补图 ;
3.找哈密顿道路 : 在补图中中找到一个哈密顿道路即可 , 道路沿线顶点就是每天考试课程 ;

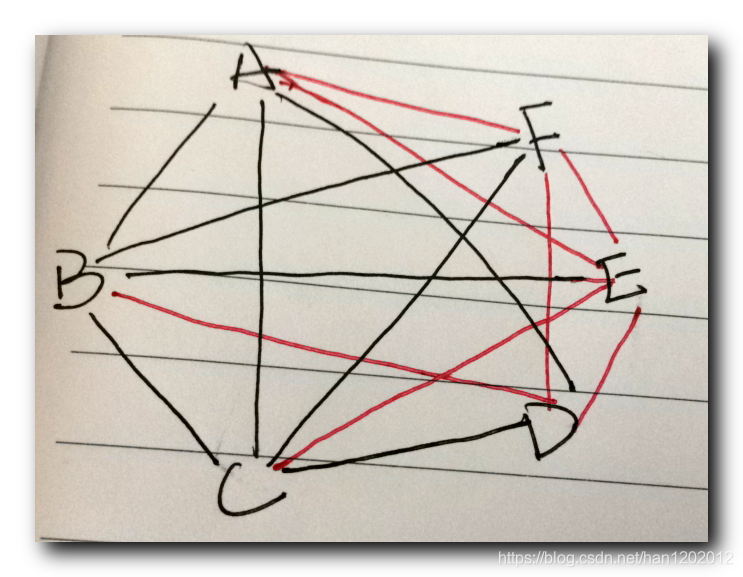
黑色的边是共同选修的课程连接在一起 ;

红色的边是补图 ;

从红色边中找出一个哈密顿圈 , 对应的哈密顿道路就是结果 ;

哈密顿圈中 , 每个顶点都不能重复 ;

哈密顿道路为 :

B \to D \to F \to A \to E \to C

十六、完全图★

题目 :

是

个顶点的简单连通平面图 , 且每个面的度数都是

, 求此图的边数

, 面数

;

: 顶点数 ;

: 边数 ;

: 面数 ;

d_{all}

: 所有面度数之和 ; 公式 1 :

2e = d_{all}

, 设

是有限平面图 , 面的次数之和 等于边数 的两倍 公式 2 :

v -e + r = 2

公式 3 :

是平面图

\Rightarrow

e \leq 3v - 6

助记 : 三角形 : 3 个顶点 , 3条边 , 2个面 ( 内部一个面 , 外部一个面 )

涉及到的相关概念 :

1. 图的几个属性 : 顶点数

, 边数

, 面数

, 面的度数之和

;

2. 面的度数之和是边数的两倍 :

D=2e

3. 欧拉定理 :

v -e +r = 2

解 :

① 列出方程 1 : 顶点数

v=n

, 每个面度数是

, 那么度数之和是

;

先根据面的度数之和 = 边数两倍写出方程 :

3r = 2e

r=\cfrac{2e}{3}

② 列出方程 2 : 根据欧拉定理

v-e+r=2

写出下面方程

n-e+r=2

③ 解方程 : 使用

表示

e,r

即可 ;

n-e+\cfrac{2e}{3}=2

e=3(n-2)

r=\cfrac{2e}{3} =2(n-2)

十七、握手定理题目★

题目 : 证明空间中不可能存在这样的多面体 , 其面数是奇数 , 每个面都由奇数条线段围成 ;

证明 :

① 用反证法 , 假设存在这样的多面体

, 其面数是奇数 , 每个面都有奇数条线段围成 ;

将空间中的多面体与平面中的平面图建立一一对应关系

② 构造多面体及对应的图 : 构造图 : 如果有这样的多面体 , 以此多面体的面集合为顶点 , 构造图

; 构造图中连线标准 : 当且仅当

中两个面有公共边界时 , 才能在

中两个面对应的两个顶点之间连一条边 ;

③ 提取关键信息 : 提取其中构造图

的顶点个数和顶点的度信息 ;

有奇数个面 , 代表着

有奇数个顶点 ,

中每个面都有奇数条线段 , 代表

中每个点的度数都是奇数 ;

④ 使用握手定理证明该假设不成立 : 握手定理 : 图的所有顶点度数之和等于边的两倍 ; ★ 握手定理推论 : 奇数个顶点的个数必定是偶数个 ; ★

图

中顶点的个数是奇数个 , 每个顶点的度是奇数 , 与握手定理及推论冲突 , 假设不成立 ; 因此这种多面体不存在 ;

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2019-07-22，如有侵权请联系 cloudcommunity@tencent.com 删除

遍历

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体同步曝光计划，欢迎热爱写作的你一起参与！

登录后参与评论

0 条评论

热度