ICML 2023 | LSM：基于隐谱模型的高维偏微分方程求解器

本文约4000字，建议阅读5分钟本文介绍本组ICML 2023 科学学习方向的最新工作：Solving High-Dimensional PDEs with Latent Spectral Models。

摘要：针对高维PDE求解过程中的高计算复杂度与复杂映射拟合的难题，本文提出了隐谱模型（LSM），在理论保证下实现了复杂映射的高效、准确近似，并在广泛的固体、流体模拟任务上取得了一致最优结果。

作者：吴海旭，胡腾戈，罗华坤，王建民，龙明盛

链接：https://arxiv.org/pdf/2301.12664.pdf

代码：https://github.com/thuml/Latent-Spectral-Models

1. 引言

现实世界中许多现象都是由偏微分方程（PDE）控制的，例如湍流、大气环流、材料形变等。因此，求解PDE是科学与工程领域共有的基础性问题，对飞机设计、气象预报、建筑承重测试等重大需求至关重要。

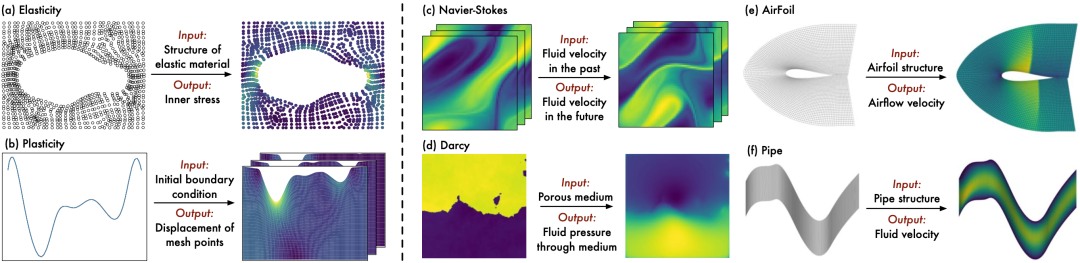
PDE控制任务：固体模拟（左）；流体模拟（右）

在现实应用中，PDE通常首先被离散化至高维坐标空间（Coordinate Space）中，例如点云（Point Cloud）、网格（Mesh）、柵格（Grid）等，再使用数值方法求解。如上图所示，由Navier-Stokes控制的流体模拟任务可以被离散化为连续的柵格图像，其坐标空间的维度则等于连续帧中像素的个数，即对于帧的图像而言，其所在的坐标空间的维度为。

然而，上述坐标空间的高维属性为PDE的求解过程带来了严峻挑战：

• 巨大的计算开销：数值方法在高维空间中的求解过程将随着维数的增加，计算量呈指数倍增长，即维数灾难现象。
• 复杂输入-输出映射：由于PDE控制的任务往往存在多过程、多物理量的耦合，输入输出之间的映射关系极其复杂，难以通过简单的深度模型准确拟合。

因此，如何高效、准确地近似高维空间中复杂的输入输出映射是使用深度模型求解PDE的关键问题。

为解决上述挑战，我们提出了隐谱模型（Latent Spectral Models，LSM），该模型具有以下特点：

• 摆脱了冗余的坐标空间，在紧凑的隐空间（Latent Space）中高效地求解PDE；
• 受经典谱方法（Spectral Methods）启发设计，实现了理论保证下的通用近似能力和优秀的收敛性质；
• 在广泛的固体、流体建模任务上取得一致最优结果，误差平均降低11.5%，并表现出优秀的效率与迁移性质。

2. 问题分析

2.1 基础知识

问题定义：依照神经算子（Neural Operator）领域的惯例，我们将数据定义为关于坐标值的函数。具体地，对于给定的维坐标空间，PDE控制任务对应的输入为，输出为。具体地，对于一张栅格图像而言，为二维坐标空间中的方形网格点集合，则表示图像在位置处的数值。

在上述定义下，PDE求解任务可以被形式化为使用深度模型拟合算子，其中，分别为输入和输出函数所在的Banach空间。

谱方法（Spectral Methods）是一类被广泛使用的PDE数值求解方法。其关键设计为使用有限正交基函数（basis functions）的和来近似PDE的解，即

其中为正交基函数，为超参数，为基函数的系数。

通过上述近似，PDE的求解过程即可被简化为优化系数，使得可以更好地满足PDE约束。在PDE求解中，谱方法具有优秀的近似和收敛性质。

2.2 设计思路

此前已有许多深度模型被用于求解PDE，但是它们往往局限在高维坐标空间中，且仅仅使用单一深度模型近似输入输出映射。这使得求解过程面临着大量冗余信息，以及随之而来的巨大计算开销和复杂映射拟合等诸多挑战。

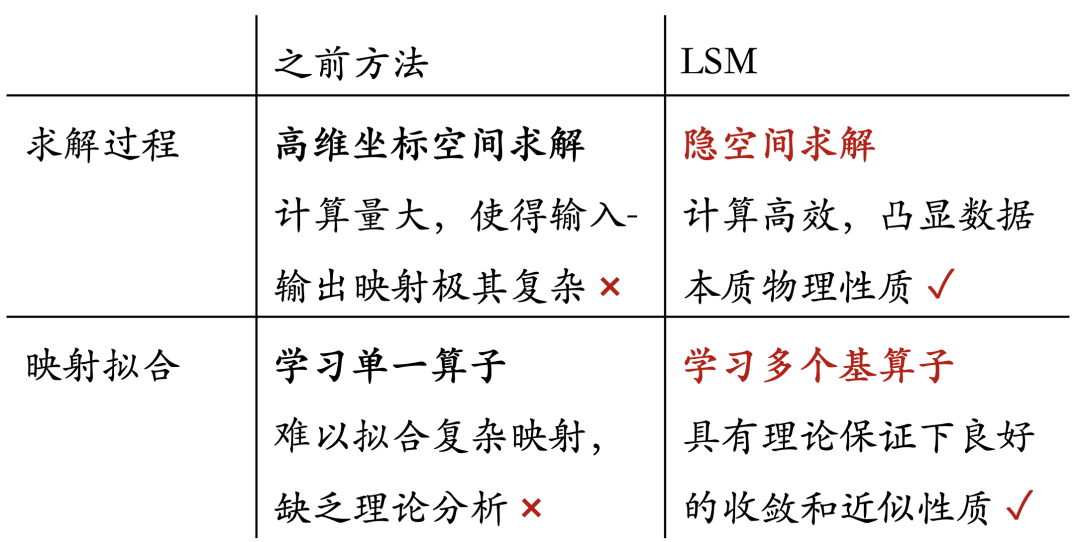
LSM与之前方法对比

我们观察到，PDE控制的数据虽然表现出的状态各不相同，但均受到统一物理方程的约束。这启发我们：这些高维坐标空间的数据其实可以被投影到更加紧凑的隐空间中。

因此，在LSM中，我们提出了层次化投影网络（Hierarchical Projection Network），使得模型可以以线性复杂度将高维坐标空间投影至隐空间，进而进行方程求解。在这一过程中冗余的坐标信息被丢弃，关键的物理属性将被更加凸显出来。

同时为了拟合复杂映射，受到数值分析中经典谱方法的启发，我们提出了神经谱单元（Neural Spectral Block），使得LSM不再仅仅学习单一的算子，而是将复杂的非线性映射分解为多个基算子。这种在隐空间中学习基算子的设计使得LSM具有了理论保证下优秀的近似和收敛性质。

3. Latent Spectral Models

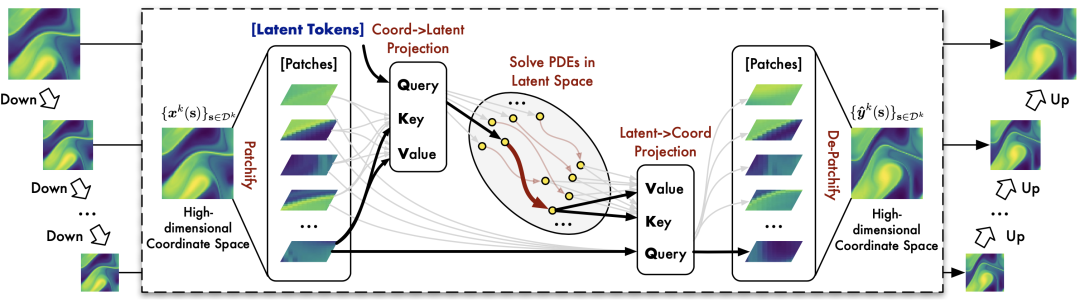
LSM整体架构

如上图所示，得益于隐空间的引入，LSM的求解过程可以摆脱冗余的坐标空间，其求解过程可以表示为：

其中，表示模型参数，与表示隐空间与坐标空间之间的投影，由层次化投影网络完成。表示在隐空间中的求解过程，由神经谱单元完成。

3.1 层次化投影网络

如上图所示，为了将高维坐标空间投影至隐空间，我们提出了基于注意力的投影方法（Attention-based projectors）。注意，如果我们直接应用标准的注意力机制，那么处理结果将仍然在坐标空间中。因此，我们引入了多个独立的隐令牌（Latent Tokens）作为注意力机制的查询项。

隐令牌的引入使模型可以以线性复杂度完成投影，同时因为隐令牌为深度模型参数（在所有的数据中共享），所以它将会在模型优化过程中学习数据的共有特征，即PDE约束，从而为投影过程提供物理信息提示。

具体地，对于坐标空间内的深度特征，我们随机初始化个独立的隐令牌用于投影。以下为投影过程：

（1）坐标空间隐空间（CoordToLatent）：我们将隐令牌作为查询（Queries），输入特征作为键值（Keys）和数值（Value），则投影过程可以表示为：

其中，，为线性层。

表示相似度计算。通过上述过程，在隐令牌的提示下，高维坐标空间中的特征被投影到个输入隐令牌。

（2）隐空间求解（Solve）：在通过神经谱单元在隐空间中求解后，输入隐令牌被映射到了输出隐空间中的令牌。具体过程将在下一节介绍。

（3）隐空间坐标空间（LatentToCoord）：在投影回隐空间的过程中，我们将坐标空间作为查询，输出隐令牌作为键值和数值，即

至此，我们得到了输出特征。

注意到，PDE通常在不同的观测尺度和观测区域表现出不同的物理状态。例如，在下图所表示的湍流中，非定常旋涡呈现不同的尺度，它们互相交互，使得物理过程非常复杂。为了应对PDE本质的多尺度属性，我们提出了分块多尺度架构（Patchified multiscale architecture），将上述投影和求解过程应用于不同层次的局部区域中，从而在不同区域和不同尺度中求解PDE。

湍流中的多尺度结构示例

3.2 神经谱单元

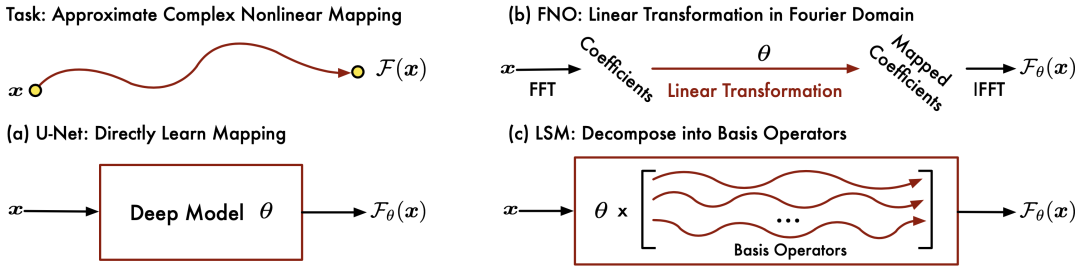
不同模型的映射拟合方式对比

为了拟合复杂映射，不同于之前学习单一算子的方法，受到经典谱方法的启发，我们设计了神经谱单元（Neural Spectral Block）。如上图所示，神经谱单元将复杂映射分解为多个基算子用于复杂映射的近似，即：

其中为超参数，表示正交基算子，为可学习参数。遵循谱方法中的经典设计，我们选取三角基算子进行实现：对于输入的函数，，我们如下定义基算子：

其中，，是偶数。

具体地，给定输入隐令牌，则输出隐令牌的计算方式为：

其中，为可学习参数，并使用残差链接便于模型优化。

我们将上述神经谱单元的求解过程定义为：。特别地，因为不同尺度上的PDE方程具有不同的系数，因此模型参数在不同层次之间独立，但在同一层次不同区域分块间共享。

由于PDE约束已经被蕴含在输入-输出数据中，随着深度模型的训练，将不断被优化，即求解PDE。此外，神经谱单元的设计也使得LSM具有了通用拟合能力。

3.3 收敛性质分析

接下来，我们将从高维谱方法开始分析，进而说明LSM设计对于复杂映射拟合的优势。

高维空间谱方法的收敛性分析：对于维空间中的周期函数，，, ，如果直接在高维空间中使用谱方法进行拟合，其三角近似为：

若满足Lipschitz条件，则存在常数，使得

值得注意的是，上述定理并没有给出高维谱方法的有效上界，因为即使是在非常简单的栅格图像中（），上述不等式给出的高维谱方法的收敛性质也很差。更进一步，目前学界也并没未给出谱方法在高维空间中的收敛性保证。

神经谱单元的收敛性分析：得益于隐空间的引入，我们将高维空间投影至独立的隐令牌中，且在不同的通道间进行独立的近似。上述设计使得谱方法可以作用在一维隐空间中，从而有效地了优化模型的收敛性质。

具体地，对于函数，如果其满足Lipschitz条件，则通过神经谱单元得到的近似函数（具有残差连接的三角近似）一致收敛于，且收敛速度为：

其中，为常数。上述定理表明，在隐空间中使用神经谱单元进行求解，可以实现优秀的近似和收敛性质。详细的理论分析及证明请见论文。

4. 实验

如下图所示，我们将LSM在7个广泛使用的数据集中进行了测试，涵盖了多样的输入格式，以及流体、固体模拟任务。

同时我们将LSM与13个基线模型进行了细致对比，包含经典的FNO（2021）等方法，也有U-NO（2022）、F-FNO（2023）以及HT-Net（2023）等最新工作。

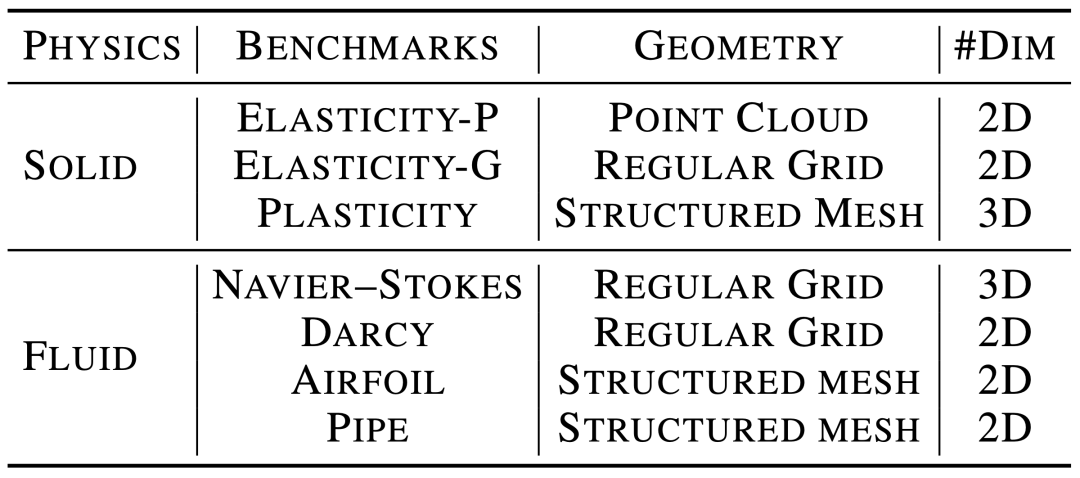
实验数据集

4.1 主要结果

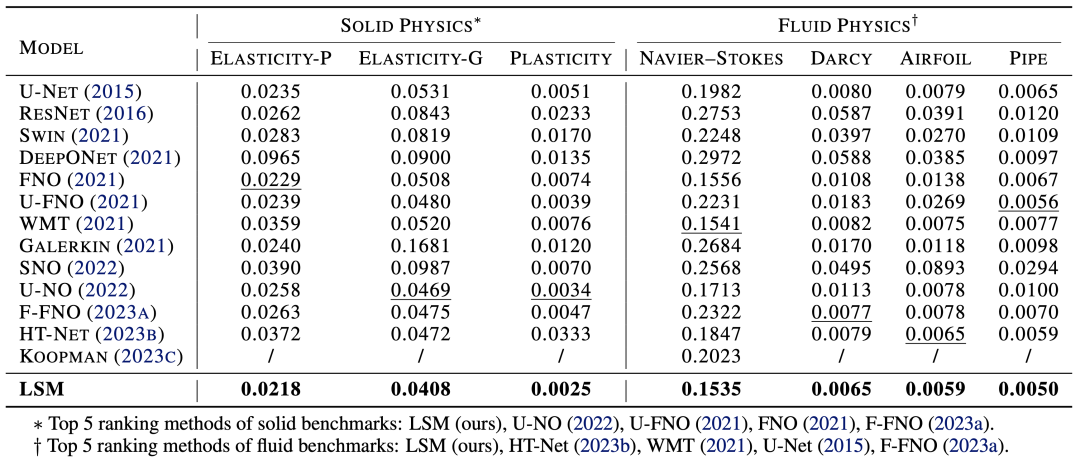
不同模型在7个任务上的均方误差（MSE）比较

如上表所示，LSM在7个任务上取得了一致的最优结果。同时，与各个数据集上之前的SOTA方法相比，MSE平均降低了11.5%。

值得注意的是，因为流体和固体物理性质差别较大，所以在这两类任务中，效果排名前五的模型具有较大差别。而LSM可以在两类任务上均取得最优的结果，体现了模型对于复杂映射的通用近似能力。

4.2 样例分析

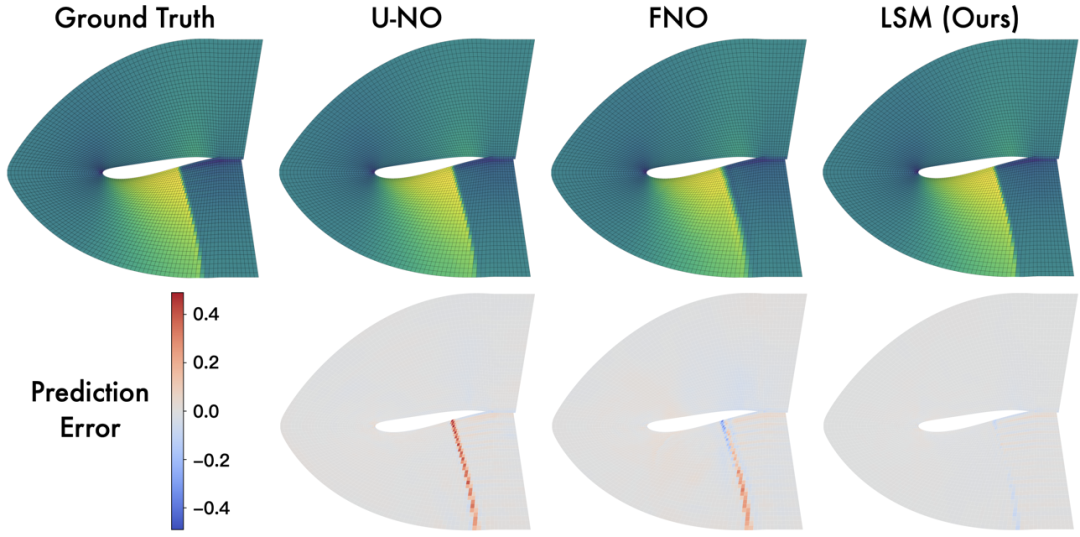
机翼周围风速估计

为了直观对比不同模型的效果，我们在上图中展现了不同模型对于机翼周围风速估计的效果。由于机翼的特殊结构，其周围会存在激波，而LSM可以准确捕捉这一特殊的物理现象，对于实际应用十分重要。

4.3 效率分析

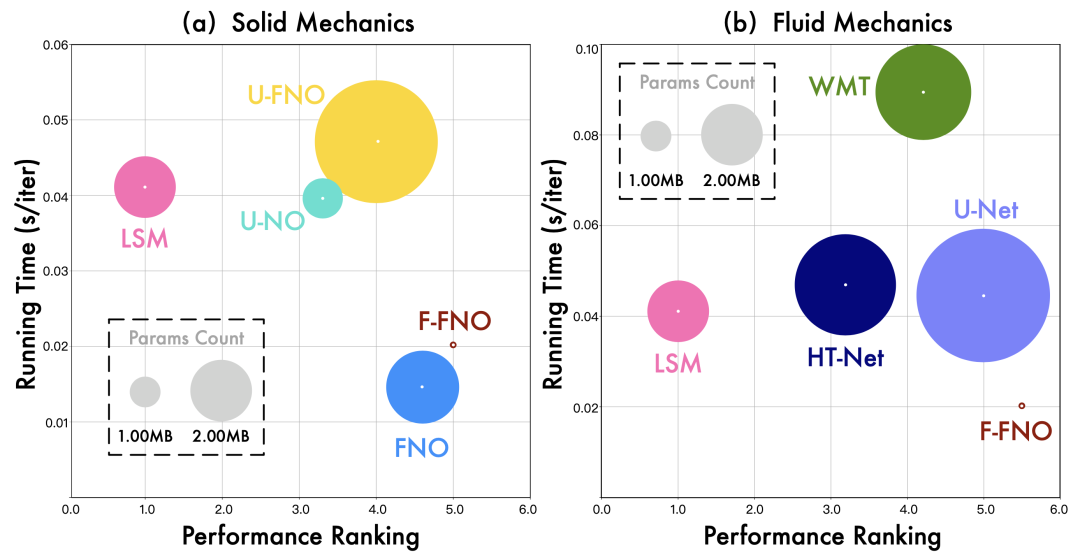
横轴：模型效果排名；纵轴：运行时间。

如上图所示，我们分别展示了固体和流体数据集上效果排名前五模型的计算效率情况。从中可以看到LSM除了取得一致的最优效果外，还在运行时间和模型参数量上得到了较好的平衡。

4.4 求解过程可视化

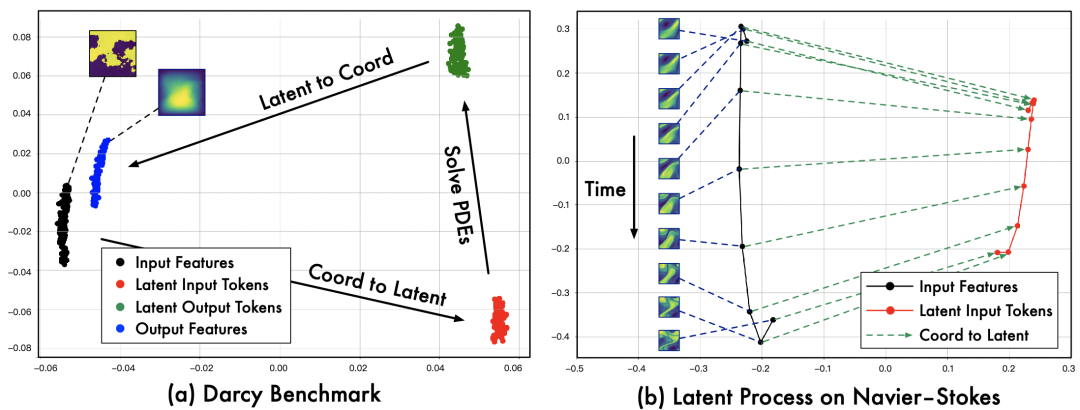
特征PCA降维可视化

我们对模型的深度特征以及隐令牌进行了PCA降维，上述可视化可以较为清晰地展现LSM的求解过程：

• 在Darcy数据集上（输入输出异质），LSM准确学习到了隐空间中较为明显的特征变换。
• 在Navier-Stokes数据集上（预测流体未来速度变化），LSM可以较好地捕捉到数据在隐空间中随时间的变化。

4.5 模型迁移

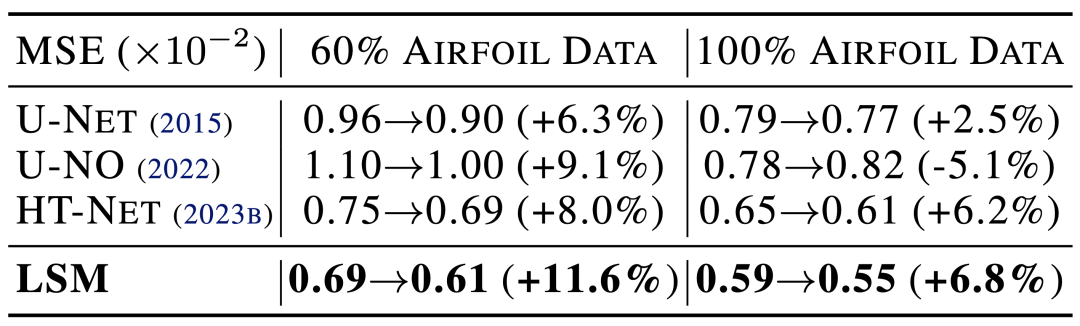
将Pipe预训练模型迁移至Airfoil上的MSE变化

进一步，我们测试了模型对于不同边界条件的迁移能力。如上表所示，LSM可以在管道流体（Pipe）和机翼风速（Airfoil）间完成高效的模型迁移，且在小数据和全量数据上均取得了显著的效果提升。

5. 总结

针对高维PDE求解这一关键科学问题，本文提出了隐谱模型（LSM），创新地将PDE求解过程投影至隐空间，并通过学习多个基算子实现了理论保证下高维复杂映射的高效、准确模拟。

LSM在广泛的固体和流体数据集上取得了一致最优结果，并在不同边界条件的

PDE求解中表现出良好的可迁移性，对于航空、气象、建筑等领域具有优秀的应用潜力。

欢迎感兴趣的朋友阅读我们的论文(https://arxiv.org/pdf/2301.12664.pdf)或者访问GitHub项目页面(https://github.com/thuml/Latent-Spectral-Models)查看更多细节内容。

编辑：黄继彦