Local Planning Path-三次螺旋曲线

YoungTimes

发布于 2023-09-25 19:16:46

6500

发布于 2023-09-25 19:16:46

文章被收录于专栏：半杯茶的小酒杯半杯茶的小酒杯

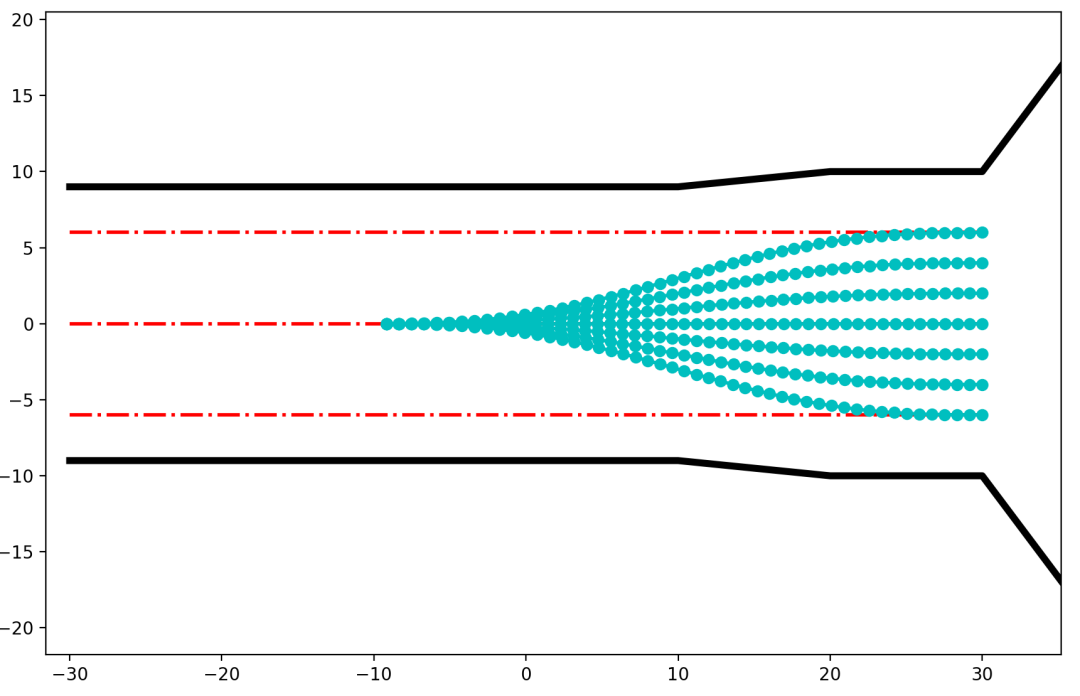
三次螺旋曲线效果

规划问题其实就是给定一个起点状态

(x_0, y_0, \theta_0, k_0)

，在满足运动学约束的前提下，找到一个达到终点状态

(x_f, y_f, \theta_f, k_f)

的路径。

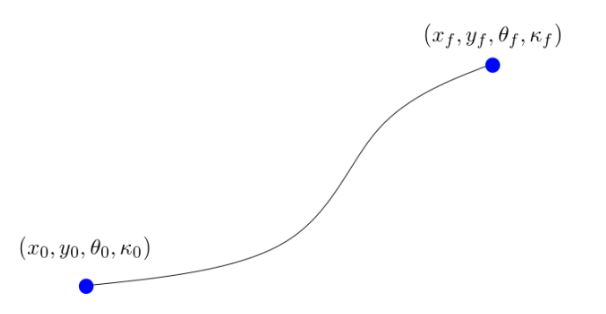
多项式螺旋线

为了简化对优化问题的表示，我们将路径定义为参数曲线，多项式螺旋线(Polynomial Spirals)是参数曲线的一种。

三次多项式螺旋线的定义如下：

k(s) = a_0 + a_1 * s + a_2 * s^2 + a_3 * s^3

它把曲率

定义为弧长

的函数。由于螺旋线是曲率的多项式函数，它的结构非常容易满足路径规划问题中的近似曲率约束，即通过限制螺旋线中几个点的曲率，就很可能满足了整个曲线上的曲率约束。

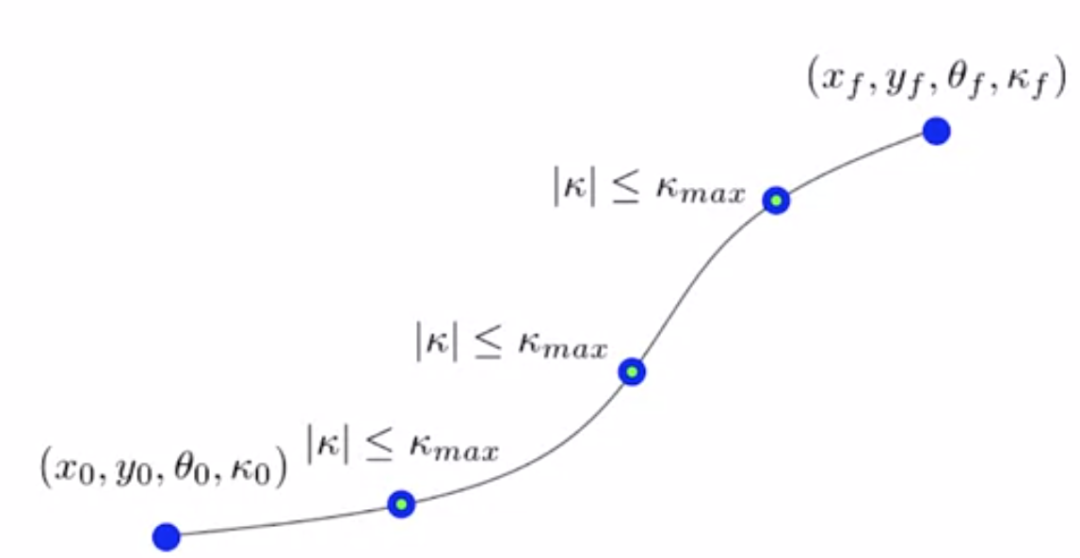
结合车辆运动学公式，可以得到:

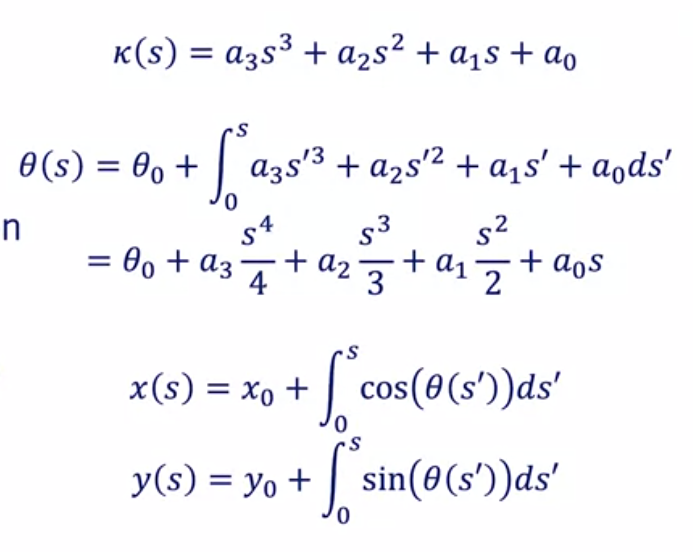
来源[2]

使用多项式螺旋的不足之处在于，螺旋线的位置和航向没有封闭解(Closed Form Solution)，必须通过迭代优化生成满足边界条件的螺旋线，用数值逼近来计算螺旋的最终端点。辛普森公式(Simpson's Rule)是其中一种常用的数值积分工具，通常比其他形式上的数值方法更加精确。

辛普森公式

辛普森公式(Simpson's Rule)是一种用于近似计算定积分的数值积分方法。

辛普森公式的具体计算公式为：

\int_a^b f(x)dx \approx h/3 [f(a) + 4f(a+h) + 2f(a+2h) + 4f(a+3h) + ... + 4f(b-h) + f(b)]

其中，h =(b-a)/n，其中n为分段的数量。

def simpson_rule(self, f, a, b, n):\ 
    """  
    f: 要积分的函数  
    a: 积分下限  
    b: 积分上限  
    n: 迭代次数  
    """  
    h = (b - a) / n  # 计算步长  
    x = [a + i * h for i in range(n + 1)]  # 生成分割点  
    y = [f(xi) for xi in x]  # 计算每个分割点处的函数值  
    
    # 根据辛普森公式进行计算  
    I = h / 3 * (y[0] + 4 * sum(y[1:-1:2]) + 2 * sum(y[2:-1:2]) + y[-1])  
    
    return I

对三次螺旋线应用辛普森公式(Simpson's Rule)，得到:

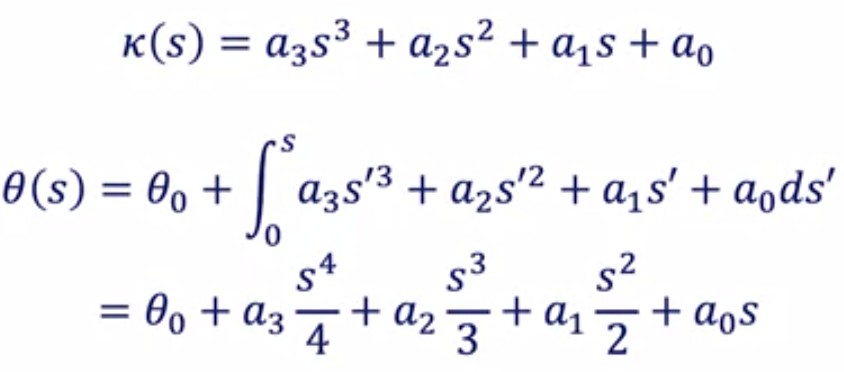
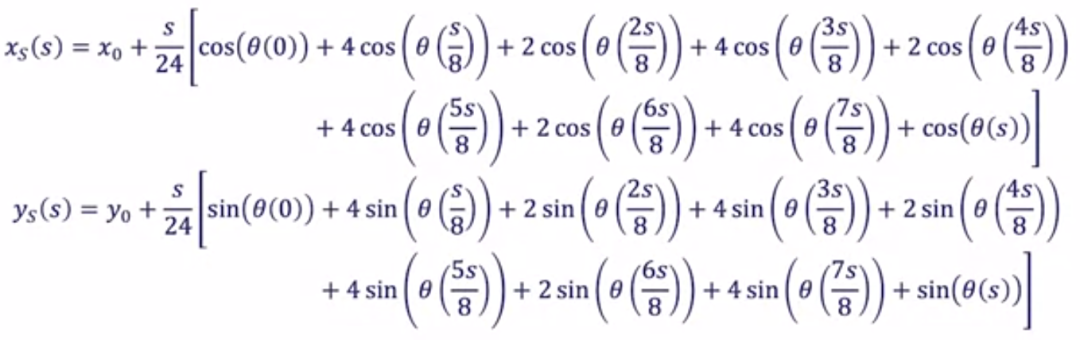
边界约束(Boundary Condition)

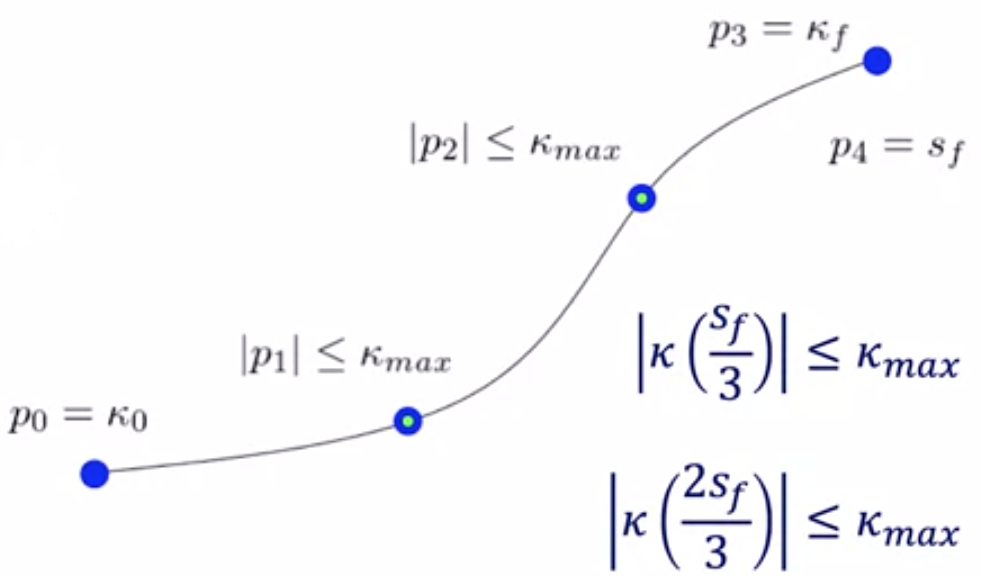
基于三次Spiral的终点边界条件约束如下：

曲率约束可以保证车辆的安全行驶和乘坐舒适性，假设汽车的最小转弯半径是2m，则局部路径的最大曲率是0.5。由于螺旋曲线的性质，只要采样几个均匀间隔的点，并对采样点施加曲率约束，就可以生成满足曲率限制的螺旋线。

优化目标函数

我们期望规划得到的路径是平稳舒适的, 这可以通过最小化我们规划的参数曲线的“弯曲能量”来完成，曲线的“弯曲能量”是指沿着路径的整个弧长的平方曲率的积分。

同时为了保证优化的最终位置和朝向与目标最终位置和朝向相同，将与目标位置和朝向的差值也作为惩罚项。

min(f_{be} (a_0, a_1, a_2, a_3, s_f) + \alpha (x_s(s_f) - x_f)^2 + \beta (y_s(s_f) - y_f)^2 + \gamma (\theta_s (s_f) - \theta_f)^2)

其中:

f_{be} = \int_{s_0}^{s_f} (a_0 + a_1 * s + a_2 * s^2 + a_3 * s^2) ds

def objective(self, p):
    p = [0.0, p[0], p[1], 0.0, p[2]]
        
    return self.fbe(p)  +  25.0 * (self.fxf(p)**2.0 + self.fyf(p)**2.0) + 30.0 * self.ftf(p)**2.0

参数重映射

三次多项式螺旋能够保持曲率的连续性，但是因为参数尺度的差异性，会导致不连续的转向率(steering rate)。在低速度场景下，该误差可以被忽略，但是在高速度场景下，会造成很大的误差。

因此，可以通过下面两种方法提高路径的稳定性

参数优化模型
五次多项式螺旋

稳定路径模型本文主要考虑参数化优化模型。为了建立稳定路径模型用于数值求解，定义一组新的参数为:

p = [p_0, p_1, p_2, p_3, s_f]

并根据：

k(0) = p_0

k(s_f / 3.0) = p_1

k(s_f * 2.0 / 3.0) = p_2

k(s_f) = p_3

得到：

不难发现:

p_0 = k_0

p_3 = k(s_f)

因此只要通过优化方式找到三个参数

p = [ p 1 , p 2 , s f ]

。

Python优化求解

SciPy优化库可以用来解决通用非线性优化问题。

result = scipy.optimize.minimize(objective_function, 
                     x_0,
					 method='L-BFGS-B', 
                     jac=objective_jacobian,
					 bounds=bounds, 
                     options={'disp' : True}
                     )

其中需要提供Jacobin矩阵。目标函数的Jacobin函数如下：

def objective_grad(self, p):
    p = [0.0, p[0], p[1], 0.0, p[2]]

    return np.add(np.add(np.add(self.fbe_grad(p), np.multiply(25, self.fxf_grad(p))), \
            np.multiply(25, self.fyf_grad(p))), np.multiply(30, self.ftf_grad(p)))

jacobin推导过程中，对

s_f

的偏导推了好多遍才算对。

目标函数fbe部分的Jacobin计算：

   def fbe_grad(self, p):
        grad = [0.0, 0.0, 0.0]

        num = self._integrate_steps

        delta = (p[4] - self._s0) / num

        for i in range(num + 1):
            s = self._s0 + i * delta

            param = delta / 3.0 
            if (i > 0 and i != num and i % 2 == 0):
                param = param * 2

            elif (i > 0 and i != num and i % 2 == 1):
                param = param * 4

            # print(self.curvature(s, p))

            grad[0] += (9.0 / p[4] * s \
                - 22.5 / (p[4]**2) * s**2 \
                + 13.5 / (p[4]**3) * s**3) * self.curvature(s, p) * 2.0 * param

            grad[1] += (-9.0 / (2 * p[4]) * s \
                + 18.0 / (p[4]**2) * (s**2) \
                - 27.0 / (2 * p[4]**3) * (s**3)) * self.curvature(s, p) * 2.0 * param

            grad[2] += (1.0 / (p[4]**2) * (5.5 * p[0] -9.0 * p[1] + 4.5 * p[2] - p[3]) * s \
                - 2.0 / (p[4]**3) * (9 * p[0] - 22.5 * p[1] + 18 * p[2] - 4.5 * p[3]) * (s**2) \
                + 3.0 / (p[4]**4) * (4.5 * p[0] - 13.5 * p[1] + 13.5 * p[2] - 4.5 * p[3]) * (s**3)) * self.curvature(s, p) * 2.0 * param


        return grad

目标函数x部分的Jacobin计算：

def fxf_grad(self, p):
    grad = [0.0, 0.0, 0.0]

    num = self._integrate_steps

    delta = (p[4] - self._s0) / num

    grad_2_1 = 0.0
    grad_2_2 = 0.0

    grad_2_param = 1.0


    for i in range(num + 1):
        s = self._s0 + i * delta

        param = delta / 3.0 
        if (i > 0 and i != num and i % 2 == 0):
            param = param * 2
            grad_2_param = 2.0

        elif (i > 0 and i != num and i % 2 == 1):
            param = param * 4
            grad_2_param = 4.0

        grad[0] += (-9.0 / p[4] * (s**2 / 2.0) \
                + 22.5 / (p[4]**2) * (s**3 / 3.0) \
                - 13.5 / (p[4]**3) * (s**4 / 4.0)) * np.sin(self.theta(s, p)) * self.fxf(p) * 2 * param

        grad[1] += (4.5 / p[4] * (s**2 / 2.0) \
                - 18.0 / (p[4]**2) * (s**3 / 3.0) \
                + 13.5 / p[4]**3 * (s**4 / 4.0)) * np.sin(self.theta(s, p)) * self.fxf(p) * 2 * param


        grad_2_1 += (-1.0 / (p[4]**2) * (5.5 * p[0] - 9.0 * p[1] + 4.5 * p[2] -  p[3]) * (s**2 / 2.0) \
                + (2.0 / (p[4]**3)) * (9 * p[0] - 22.5 * p[1] + 18.0 * p[2] - 4.5 * p[3]) * (s**3 / 3.0) \
                - (3.0 / (p[4]**4)) * (4.5 * p[0] - 13.5 * p[1] + 13.5 * p[2] - 4.5 * p[3]) * (s**4 / 4.0))  * np.sin(self.theta(s, p)) * param


        grad_2_2 += 1.0 / (3.0 * num) * np.cos(self.theta(s, p)) * grad_2_param

    grad[2] = (grad_2_1 + grad_2_2) * self.fxf(p) * 2 


    return grad

目标函数y部分的Jacobin计算：

   def fyf_grad(self, p):
        grad = [0.0, 0.0, 0.0]

        num = self._integrate_steps

        delta = (p[4] - self._s0) / num

        # tst = 0.0

        grad_2_1 = 0.0
        grad_2_2 = 0.0

        for i in range(num + 1):
            s =  self._s0 + i * delta

            # print("i="+str(i))

            param = delta / 3.0 
            grad_2_param = 1.0
            if (i > 0 and i != num and i % 2 == 0):
                param = param * 2
                grad_2_param = 2.0

            elif (i > 0 and i != num and i % 2 == 1):
                param = param * 4
                grad_2_param = 4.0

            grad[0] += (9.0 / p[4] * (s**2 / 2.0) \
                - 22.5 / (p[4]**2) * (s**3 / 3.0) \
                + 13.5 / (p[4]**3) * (s**4 / 4.0)) * np.cos(self.theta(s, p)) * 2 * self.fyf(p) * param

            grad[1] += (-4.5 / p[4] * (s**2 / 2.0) \
                + 18.0 / p[4]**2 * (s**3 / 3.0) \
                - 13.5 / p[4]**3 * (s**4 / 4.0)) * np.cos(self.theta(s, p)) * 2 * self.fyf(p) * param

            grad_2_1 += ((1.0 / p[4]**2.0) * (11.0 / 2.0 * p[0] - 18.0 / 2.0 * p[1] + 9.0 / 2.0 * p[2] - p[3]) * (s**2 / 2.0) \
                - (2.0 / p[4]**3.0) * (9.0 * p[0] - 22.5 * p[1] + 18.0 * p[2] - 4.5 * p[3]) * (s**3 / 3.0) \
                + (3.0 / p[4]**4.0) * (4.5 * p[0] - 13.5 * p[1] + 13.5 * p[2] - 4.5 * p[3]) * (s**4 / 4.0)) * np.cos(self.theta(s, p))  * param \

            grad_2_2 += 1.0 / (3.0 * num) * np.sin(self.theta(s, p)) * grad_2_param


        grad[2] = (grad_2_1 + grad_2_2) * 2 * self.fyf(p)


        return grad

目标函数

\theta

部分的Jacobin计算：

    def ftf_grad(self, p):
        grad = [0.0, 0.0, 0.0]

        s = p[4]

        grad[0] += 9.0 / p[4] * (s**2 /2.0) * 2 * self.ftf(p) \
                - 22.5 / (p[4]**2) * (s**3 / 3.0) * 2 * self.ftf(p) \
                + 13.5 / (p[4]**3) * (s**4 / 4.0) * 2 * self.ftf(p)

        grad[1] += -9.0 / (2 * p[4]) * (s**2 / 2.0) * 2 * self.ftf(p) \
                + 18.0 / (p[4]**2) * (s**3 / 3.0) * 2 * self.ftf(p) \
                - 27.0 / (2 * p[4]**3) * (s**4 / 4.0) * 2 * self.ftf(p)

        grad[2] += 1.0 / (p[4]**2) * (5.5 * p[0] - 9.0 * p[1] + 4.5 * p[2] + p[3]) * (s**2 / 2.0) * 2 * self.ftf(p) \
                - 2.0 / (p[4]**3) * (9 * p[0] - 22.5 * p[1] + 18 * p[2] - 4.5 * p[3]) * (s**3 / 3.0) *  2 * self.ftf(p) \
                + 3.0 / (p[4]**4) * (4.5 * p[0] - 13.5 * p[1] + 13.5 * p[2] - 4.5 * p[3]) * (s**4 / 4.0) *  2 * self.ftf(p)

        return grad

至此，输入目标状态

(x_f, y_f, \theta_f, k_f)

，就可以得到从起点状态到终点状态的Local Planning Path。

参考材料

1、[PathPlanning]State Lattice Plannerhttps://blog.csdn.net/qq_28366817/article/details/129330967?utm_medium=distribute.pc_relevant.none-task-blog-2~default~baidujs_baidulandingword~default-0-129330967-blog-117754864.235^v38^pc_relevant_anti_vip&spm=1001.2101.3001.4242.1&utm_relevant_index=3

2、Udacity自动驾驶课程 https://www.coursera.org/learn/motion-planning-self-driving-cars/lecture/l4Aab/lesson-1-parametric-curves

3、https://zhuanlan.zhihu.com/p/93980119?utm_id=0

本文参与腾讯云自媒体同步曝光计划，分享自微信公众号。

原始发表：2023-09-24 21:18，如有侵权请联系 cloudcommunity@tencent.com 删除

local