文章/答案/技术大牛

发布

社区首页 >专栏 >详解DDPG算法：解决对大量的超参数、随机重启、任务环境敏感问题，完成月球着陆器，双足机器人demo、以及超参数调优教学

详解DDPG算法：解决对大量的超参数、随机重启、任务环境敏感问题，完成月球着陆器，双足机器人demo、以及超参数调优教学

汀丶人工智能

发布于 2023-10-11 09:46:42

2.6K00

代码可运行

文章被收录于专栏：NLP/KGNLP/KG

运行总次数：0

代码可运行

0.demo展示

当我复现强化学习算法 DDPG 时，我发现论文中缺少必要的实现细节，例如：Gamma、噪声方差、最大训练步数等参数的取值。此外，在我调整参数，成功完成某次训练后，当我对随机种子进行修改，发现训练时长有很大变化，甚至有时候无法完成训练。更别提把在某个任务上 work 的代码换到相似任务上的艰辛历程了。

如果你被这些问题困扰，那么你可能需要这份代码。由于我找不到符合我要求的轮子（2019-08），所以我只能自己造了，我认为这份代码解决了以上问题，符合以下要求：

算法适用性广，适用于不同的任务（即便不做修改，也能完成不同的 Gym 的游戏）
算法比较简单，代码可读性强（若某个结构加入后对性能提升小，那么删去此结构）
算法训练时间短，训练稳定（训练时间不超过 1 小时，即使更换 RandomSeed）

通关双足机器人硬核版 (BipedalWalkerHardcore-v3), 训练比较快（旧记录是 10,000 + 轮）使用 IntelAC 算法，

4106 轮，1960k 步，31 小时，单 GPU

（平均分 310，target reward 是 300）（不稳定，有时候需要训练 7000 轮，3000k 步，40 小时）

训练最快 4106 轮（用 IntelAC 算法通关双足机器人硬核版）BipedalWalkerHardcore-v3_哔哩哔哩 (゜ - ゜) つロ干杯~-bilibili

此外，有一个的原创文章 kangaroo CreateAMind 在 2019-07-30 也通关了（使用了采用 state-of-the-art 的 model-free RL 算法 sac1，但是没有公布训练步数）（请注意：他们修改了 Reward 函数，将超时后 done=True 时的 - 100 改为 0），文章还分析了 OpenAI Leaderboard 上的两个解决了’BipedalWalkerHardcore-v2’ 的项目（分别是 A3C+LSTM 与 CMA-ES）。其中 A3C 需要开多个 agent 进行大量的异步交互，LSTM 可能是用来解决这个任务状态转移概率比较难以完整获取的问题。而 CMA-ES（Covariance Matrix 协方差 Adaptation Evolutionary Strategies 自适应遗传算法）则使用了遗传算法，有它的帮助，在大量交互后，获得巨大优势的个体可以很快地扩散出去（比如学会了在方格上面跳的 Agent）。如果是工业界做机器人的的可不会轻易用这种两种算法，因为会报废掉很多机器人，详细内容去看他们公众号写的文章吧，写得不错：

结果出乎我的意料，经过大刀阔斧的修改后，这份代码竟然在 OpenAI 官方的排行榜 Leaderboard 上的 3 个项目都拿了靠前的名次（使用更少的训练步数达到目标分数），如下：

Yonv1943/ElegantRL

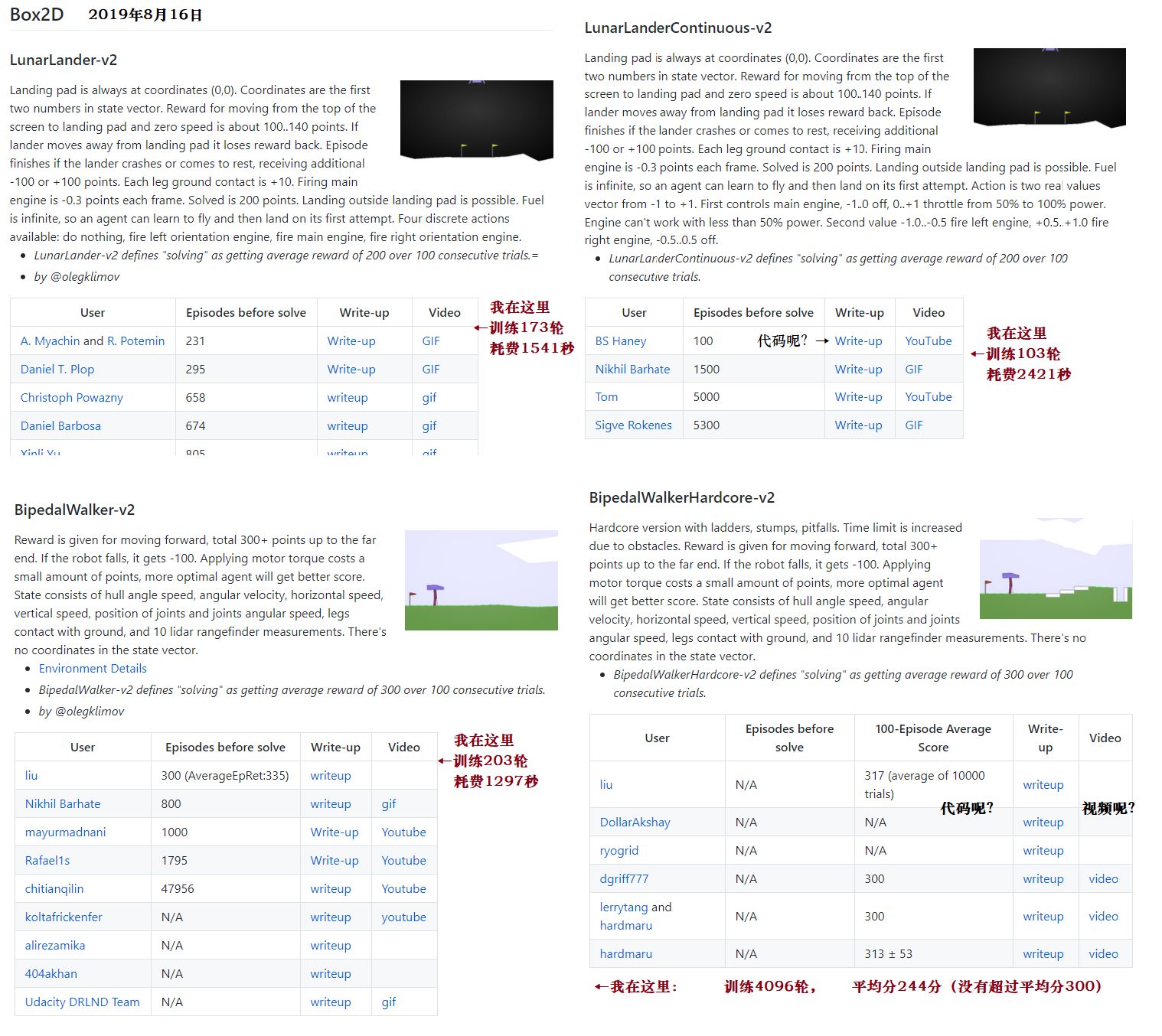
上面的代码参考了「GitHub, nikhilbarhate99 TD3 算法」，删去了 TD3 的双 actor 结构，然后把 Actor-Critic 框架当成 Generator-Discriminator 框架去训练，具体请看：

它可以不对模型进行任何修改的情况下，在下面几个 OpenAI-gym 的开游戏中，达到通关条件（硬件 RTX 2080Ti）：

月球着陆器：训练 114 轮，1231 秒（LunarLanderContinuous-v2 ，连续动作）
月球着陆器：训练 147 轮，1487 秒（LunarLander-v2 ，离散动作）
双足机器人：训练 165 轮，2011 秒（BipedalWalker-v2）
双足机器人：训练 4096 轮，28,143 秒（BipedalWalkerHardcore-v2，硬核版）平均分 244，无法达到通关条件平均分 300，若有人找到了通关此游戏的开源代码，请告诉我
正文目录
1. 原版 DDPG 的三个「敏感」：对大量的超参数、随机重启、任务环境敏感。
2. 改良 DDPG，克服「敏感」：使用延迟更新，并总结超参数选择方法
3. 如何选择强化学习的超参数：Gamma 值，训练步数，噪声方差
4. 适应连续、离散的动作
5. 适应不同的环境参数

1.原版 DDPG 的三个「敏感」：对大量的超参数、随机重启、任务环境敏感。

对**「敏感」**条件稍作修改，便会显著影响任务训练时间，甚至无法完成任务。我认为以 DDPG 为代表的 Actor-Critic 强化学习框架是具有美感的模型，让我想起了 2014 年的对抗网络（GANs），在 2015 年 GANs 刚出来的时候，也和 DDPG 一样，训练的时候非常不稳定。我想要为解决这个问题出一份力。对此的讨论请移步姊妹篇：xxxx

随机重启：换用随机种子 random seed，会使得训练时间出现波动，甚至无法收敛。根据我的观察**（猜测）**，若训练初期，误打误撞地出现了几次成功案例，那么智能体便得以快速地通关；若训练前期没有出现成功案例，那么对于一个没有好奇心的智能体，它就需要更长的训练时间，甚至会陷入自暴自弃的境地，此时增长训练时间并不能完成训练。

任务环境：通关「月球着陆器」的代码，需要进行新一轮的参数调整，才能通关「双足机器人」；通关「月球着陆器（连续版）」的代码，竟无法通关「月球着陆器（离散版）」。

大量敏感的超参数：

explore noise：探索时，需要为动作添加的噪声，此噪声的方差

γ

$\gamma$

\gamma gamma：对动作进行估值时，下一步动作的价值所占权重

τ

$\tau$

\tau tau：软更新时，该值越小，更新越 “软”

R^{(m)}

$R^{(m)}$

R^{(m)} m：记忆回放缓存的记忆容量 m （memory size）

R^{(n)}

$R^{(n)}$

R^{(n)} n：记忆回放时，进行抽样的批次大小（batch size）

M a x S t e p

$MaxStep$

MaxStep ：最大步数，若探索步数超过此最大值，则刷新环境，重新开始

对神经网络的超参数敏感：简单的任务不能用参数过多的神经网络

对应的算法如下：

=== 算法：策略梯度算法（DDPG 论文原文 ICLR 2016 [1]）===

建立两个网络：评价网络

Q (s, a | θ^{Q})

$Q(s,a|\theta^{Q})$

Q(s,a|\theta^{Q}) 以及策略网络

μ (s | θ^{μ})

$\mu (s|\theta^{\mu})$

θ^{Q} = R a n d o m I n i t (Q), θ^{μ} = R a n d o m I n i t (μ)

$\theta^{Q} = RandomInit(Q), \theta^{\mu} = RandomInit(\mu) \quad$

随机初始化网络的参数

$\theta^{Q'} = \theta^{Q}, \theta^{\mu'} = \theta^{\mu} \quad$

复制得到完全相同的两个目标网络

$Q', \mu'$

（用于软更新）

$R^{(m)} = \{s, a, r,s'\}^m_{i-1} \quad$

初始化记忆回放缓存，m 为记忆容量

For e=1, 最大训练次数 do

$\quad s_1 = Env.reset() \quad$

初始化环境，并得到初始状态

$\quad$

\quad For t=1, 最大步数 do

$\qquad a_t = \mu(s_t|\theta^{\mu}) \quad$

选择动作

$\qquad a_t =a_t+ Norm(ExploreNoise) \quad$

添加噪声，进行探索

$\qquad s_{t+1}, r_t = env.step(a) \quad$

与环境进行交互，得到状态与收益

$\qquad R.store(s_t, a_t,r_t,s_{t+1}) \quad$

保存到记忆 R 里面

$\qquad R^{(n)} = R.sample(n) \quad$

从记忆中抽样

$\qquad y_i = r_i + \gamma Q'(s_{i+1}, \mu'(s_{i+1}|\theta^{\mu'})|\theta^{Q'}) \quad$

使用评估网络进行对动作进行估值

$\qquad$

\qquad 更新评估网络与策略网络的参数

$\qquad \mathcal{L}_{Q} = \frac{1}{n}\sum^n_i \big( y_i - Q(s_i,a_i|\theta^{Q}) \big)^2 \quad$

\qquad \mathcal{L}_{Q} = \frac{1}{n}\sum^n_i \big( y_i - Q(s_i,a_i|\theta^{Q}) \big)^2 \quad 计算估值与记忆的差别

$\qquad \mathcal{L}_{\mu} = \nabla_{\theta^{\mu}}\mathcal{J} \approx \frac{1}{n}\sum^n_i \bigg( \nabla_a Q(s, a|\theta^Q)|_{s=s_i, a=\mu(s_i)} \nabla_{\theta^{\mu}}\mu(s|\theta^{\mu})|_{s_i} \bigg) \quad$

$\qquad Q.update(\mathcal{L}_Q), \mu.update(\mathcal{L}_{\mu}) \quad$

根据梯度更新参数

$\qquad \theta^{Q'} = \tau \theta^{Q} + (1-\tau)\theta^{Q'} \quad$

软更新目标评价网络的参数

$\qquad \theta^{\mu'} = \tau \theta^{\mu} + (1-\tau)\theta^{\mu'} \quad$

软更新目标策略网络的参数

$Save(\mu') \quad$

输出目标动作网络

翻译约定：

Actor Network 策略网络（演员：根据策略输出动作）
Critic Network 评估网络（评论家：根据状态，评估动作的价值）
soft update 软更新

$x' = \tau x + (1-\tau) x$

replay buffer 记忆回放缓存

2.解决 DDPG 的三个「敏感」

我参考了其他开源代码，得到了 DelayDDPG，因为它与原版 DDPG 相比，最大的不同是：它采用了延迟更新、软更新、设置更新间隔，科学计算超参数的方法，这使得强化学习算法变稳定。

**2.1 为何延迟更新，可以使强化学习算法变得更加稳定？**举月球登录器为例，我是这样解释的：现在有两种登陆的策略：

稳妥策略（降低月球登录器的移动速度，慢慢靠近地面，防止坠毁）
激进策略（只通过喷气维持平衡，接近地面时发动机全开，节省燃料）

这两种策略，都可以达到任务要求（任务要求：在连续的 100 次任务中，平均分超过 200，安全着陆且节省燃料会得到高分）。若当前状态 state 是：月球登陆器以较快的速度往下掉落，但是登录器姿态平稳，并且其距离地面还有一段距离。而策略网络的动作 action 是：不喷气，让它自由落体。那么此时评估网络应给这个 state-action 一个怎样的分数？

给低分惩罚，不喷气会增大坠毁风险，要稳一点（稳妥策略）
给高分鼓励，不喷气能节省燃料，我可以浪（激进策略）

我认为，只有当评估网络和策略网络采用相同的策略，对智能体的训练才能足够稳定，评估网络对于一个同一个 state-action 可以在训练的不同时期有不同的评估结果，但是在某一段时期内，一定要稳定，不应该发生太大的改变（陟罚臧否，不宜异同）。相比于原版 DDPG，DelayDDPG 修改了参数的更新方法，如图：

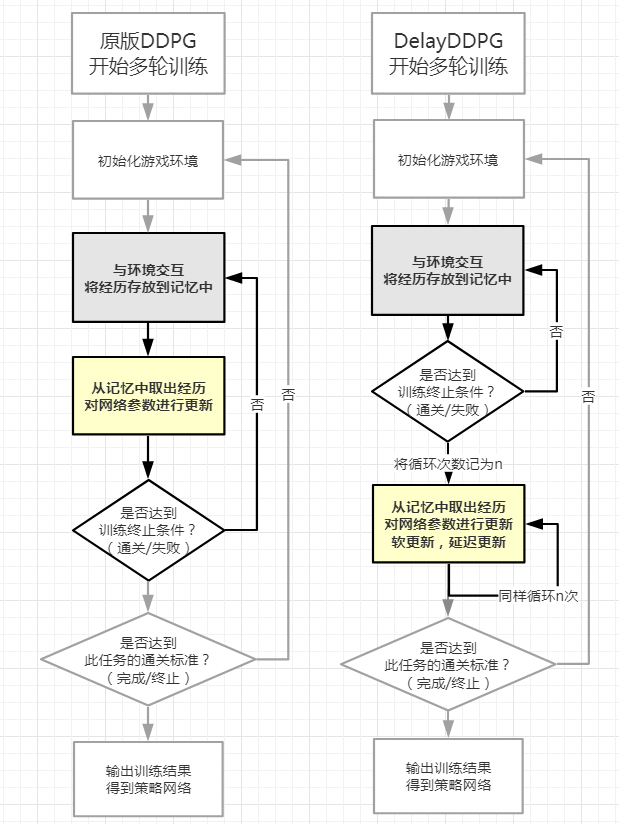
**2.2 「延迟更新」**可以稳定评估网络对 state-action 的判断。如果评估网络不断地变换战略目标，那么策略网络作为动作的实行者，将会陷入混乱。若每轮训练开始前，我先把策略网络固定下来（采用相同的策略）。等这一轮训练完成后，我再进行回忆，然后提升评估的精度，并修改我的策略。

稳定的训练过程，能够少走弯路，最终降低平均训练时间。我们可以看到一些改良算法也是这么做的。如：TRPO（Trust Region Policy Optimization），为了保证策略梯度的每一次优化，都能使网络变得更好，因此要保证在合适的步内进行参数更新，那么在这个合适的步长内内达到的区域就是信任域（Trust Region）。只要在信任域内进行策略的更新，就能保证策略稳定（更新前后，策略不会剧变）。后来的近端策略优化（PPO：Proximal Policy Optimization，2017）是对 TRPO 的改进版本，利用近似，简化了计算，成为了强化学习的一个基线模型（baseline）。

还有很多稳定训练的技巧（「设置更新间隔 update gap」，「使用软更新 soft update」，这些方法不等同于减少学习率），我也都用到了 DelayDDPG 算法中去：

"""算法：延迟策略梯度算法（DelayDDPG）"""
随机初始化 策略网络Act() 与 评估网络Cri()
为了软更新，因此我们复制得到一模一样的两个目标网络 Act'() 与 Cri'()
选择合适的损失函数 Criterion()
初始化记忆缓存R，设置最大记忆容量为m

for e in range(最大训练次数)：
  s = env.reset() 初始化环境，得到初始状态s
  for t in range(最大步数)：
    a = Act(s) 让策略网络根据状态输出动作
    a += explore_noise 在探索环境时添加噪声（epsilon-Greedy）
    s_, r, done = env.step(a) 与环境交互，得到收益与状态，任务结束时done==True
    R.store(s, r, done, a, s_) 将这些经历保存到记忆中去
    s = s_ 更新当前状态
    if done: break 若任务结束，则开始下一轮训练
  for i in range(t):  # 此处即 DelayDDPG 中的「延迟更新」
    s, r, done, a, s_ = R.sample(n) 每次从记忆中取出批次大小为n的记忆进行训练
    a_ = Act'(s_)  让目标策略网络得到下一步的动作
    a_ += polic_noise 在评估策略时，为下一步的动作添加噪声（epsilon-Greedy）
    
    q_target = r + (1-done) * gamma * Cri'(s_, a_) 使用目标评估网络评估接下来的动作
    q_eval = Cri(s, a) 将评估网络的结果与记忆对比
    Cri.update(argmin(Criterion(q_eval, q_target))) 最小化评估网络的预测误差

    a = Act(s) 离线学习，而不是通过与环境的直接交互去学习（与环境隔了一个评估网络）
    Act.update(argmax(Cri(s, a))) 最大化评估网络的估值，使用评估网络提供的梯度对策略进行优化

    update_counter += 1
    if update_counter == update_gap: 每隔一段时间，对两个目标网络进行软更新
      update_counter = 0
      Act'.p = tau * Act.p + (1-tau)*Act'.p
      Cri'.p = tau * Cri.p + (1-tau)*Cri'.p

  if r > target_reward: break 如果达到目标分数，那么训练终止
Save(Act')  训练完成后，保存目标策略网络，作为算法的输出结果

3. 如何选择强化学习的超参数？

我将代码中所有超参数都分离出来，放在 class Arguments 中，并给出了默认值。选择超参数前，你需要需要推测你的模型的**「每轮训练的步数」**。不需要准确估计，只需要数量级对得上就可以。尽管数量级是以 10 为底数，但是请注意，下面我使用 2 作为底数。

以月球登录器为例，我们可以使用未经训练的模型，测得坠毁需要的步数：
[68,142,72,99,73,89,197,59,88,59,92,93,64,81] ~= 91（2 ** 7）
那么我们猜测，平稳降落需要的步数将会和坠毁需要的步数处在相同数量级，也是2 ** 7

根据「每轮训练的步数 S」来制定多个超参数。以月球登录器为例，S 取 128（2**7）

3.1 「gamma」

*决策网络会做出让评估网络给出高评分的动作，评分的计算会使用到 gamma。为了体现决策的连续性，我们希望决策网络根据状态 state 选择动作 action 时，不仅要考虑这一步的收益，也要考虑这么做之后接下去几步的收益（下一步的局势）。根据 gamma 计算出来的 q 值，代表了这一步的质量（quality）。

q_target = r + gamma * Cri'(s_, a_)
q_eval   = Cri(s, a)
然后训练评估网络Cri()，使得 q_eval 接近于 q_target

令 q0 = Cri(s, a) ~= r0 + gamma * Cri'(s_, a_)
有 q1 = Cri(s_, a_) = r1 + gamma * Cri'(s__, a__)
则 q0 = r0 + gamma * Cri'(s_, a_)
      = r0 + gamma * q1
      = r0 + gamma * (r1 + gamma * q2)
      = r0 + gamma * (r1 + gamma * (r2 + gamma * q2))
      ... 迭代 ...
      = r0*gamma**0 + r1*gamma**1 + r2*gamma**2 + ... + rt*gamma**t
      = sum([r*gamma*i for i, r in enumrate(r_list)])

对于有通关条件的任务（如：安全降落 + 100 分，坠毁 - 100 分），其训练的最后一步是否完成任务是非常重要的。如下方图左，Gamma 值越大，就越能预见更遥远的未来。此处可以看出，在这个任务中，将 Gamma 取值为 0.99 是合适的。如下方的右图蓝色折线：从浅蓝色的第 300 步可以看出这是一次失败的降落（-100），而当 Gamma 取值为 0.99 时，一个好的评估网络应该在第 150 步之前就已经提前意识到局势危急（bad state），因而在接下去的训练中，评估网络可以很好地指导策略网络，让策略网络在坠毁的前 150 步就及时地意识到自己的错误，此时采取挽救措施还来得及。在此任务中，过小的 Gamma 值（如 0.9）将使评估网络无法及时地预见未来的事件，等到大难临头才向策略网络发出预警就来不及了。

如果 Gamma 值过大也不行，因为距离现在越远，评估网络对未来的预测精度越低，其预测结果越不可信，因此我们有必要加上一个小于 1 的 gamma 值降低遥远未来的权重。有兴趣的话，可以将 Gamma 值取最大值 1.0 体验一下。

3.2 根据「每轮训练的步数 S」

计算出合适的 Gamma 值我需要使策略网络做出判断的时候，考虑关键步骤的分数

在某轮训练中的某一步的q值为 q0，则有：
q0 = r0*gamma**0 + r1*gamma**1 + r2*gamma**2 + ... + rt*gamma**t （由前面推出）
其中，t步之后的reward 在q0 中体现为 rt * gamma**t

若t取值为「每轮训练的步数S」== 128 （128为估计值）
若该项系数 gamma**t == 0.50， 那么 0.50 ** (1/t) ==  0.5 ** (1/128) ~= 0.994 
若该项系数 gamma**t == 0.10， 那么 0.10 ** (1/t) ==  0.5 ** (1/128) ~= 0.982 # notic
若该项系数 gamma**t == 0.01， 那么 0.01 ** (1/t) ==  0.5 ** (1/128) ~= 0.964 

若t取值为「每轮训练的步数S」== 400 （400为实际值）
若该项系数 gamma**t == 0.50， 那么 0.50 ** (1/t) ==  0.5 ** (1/400) ~= 0.998 
若该项系数 gamma**t == 0.10， 那么 0.10 ** (1/t) ==  0.5 ** (1/400) ~= 0.994 # notic
若该项系数 gamma**t == 0.01， 那么 0.01 ** (1/t) ==  0.5 ** (1/400) ~= 0.988

可见，若希望 S 步后将出现的关键节点的权重为一个接近 0.1 的数，那么 gamma 值的合理区间应为 0.982~0.994，因此我在月球登陆器这个任务中，选择 0.99 作为默认值。总的来说，对 gamma 值进行调整，目的是使 q 值曲线尽可能平稳，如上图左所示，橙色曲线 gamma 值过小（gamma==0），曲线陡峭，调整后的折线两端平衡**，不会在关键节点出现极端值**。另外，如果 gamma 值过大，而评估网络的预测能力较弱（特别在复杂任务下），那么对 q 值的不准确的估计会影响策略网络的训练。因此我们需要在明确物理意义后，按照上面的计算方法去确定 gamma 值，而不是像炼丹一样去调参。条件允许的情况下，还是要尽可能举起数学的火炬照亮前方的路。

3.3 「记忆容量」

是记忆回放缓存中存放的最大记忆容量，若超过最大值，那么程序会自动会删除旧的记忆以维持容量稳定。每轮训练结束后需要通过梯度下降更新参数，更新次数为本轮训练的步数。若希望每轮训练结束后，将记忆中的所有数据都被拿出来训练，则：

记忆容量 memories_size = 本轮训练的步数 * batch_size ~= S * batch_size

3.4 「最大训练步数」

若每轮训练步数超过最大值，则强行终止，并判定为任务失败，进入参数更新步骤。如果不设置最大训练步数，那么可能会训练出一个磨磨蹭蹭的智能体，如：就差一步就到终点了，但是它就是不完成任务。则：

最大训练步数 max_step = S * 10

3.5 「探索噪声的方差」

原版 DDPG 只有探索噪声，它在与环境交互，收集训练数据存放到记忆里面时，为动作添加了噪声，促使智能体多探索未知（低阶的、被动的好奇）。

3.6 「策略噪声的方差」

在探索结束后，训练开始了，从记忆里面取出数据进行训练时，在计算 q 值的时候，也添加了噪声，促使智能体做出更加稳重的动作。

举例子，训练一个智能体过桥：距离远的桥，有宽阔的桥面；距离近的桥，桥面狭窄而没有护栏。河面以下有猛萌的黎曼鲲，掉下去后，除非证明出ζ(s) 函数的所有非平凡零点都位于临界线上，否则就会被吃掉。到达终点会，并且走的路程短就会得到奖励。那么我要如何选择两个方差呢？

可以看到，选择了大的噪声方差，会让智能体选择稳妥策略（即：加了噪声也不会掉河里），始终走在安全的地方，这样的好处是评估网络对 q 值的估计变得更加准确了，训练变得更加稳定。但是过大的噪声无法训练出采用激进策略的智能体——即便智能体以精细微操走在窄桥正中间，也无济于事，在大噪声的影响下，它还是会掉河里。如果选择了小的方差，那么我们可以训练出走橙色路径的智能体（激进策略），训练也会变得不稳定。

                 经验值         激进策略 稳妥策略
「探索噪声的方差」 explore_noise 0.4       0.1
「策略噪声的方差」 policy_nose   0.8       0.2

4. 适应连续、离散的动作

OpenAI 的 gym 刚好有两个用 Box2D 模拟的环境，动作空间为连续与离散，如下：

连续动作，LunarLanderContinuous-v2，action 为两个闭区间内的浮点数，控制两对发动机，符号决定喷射方向，绝对值决定喷射力度。
离散动作，LunarLander-v2，action 为一个整数（可为 0，1，2，3），控制四个发动机，被选中的发动机将会喷气。

我选择让策略网络输出一串浮点数矢量（闭区间），可以直接作为连续动作，也可以转换为离散动作。为了方便添加噪声，我在训练阶段使用「轮盘赌」，测试阶段使用「锦标赛」。这两个词在讨论「遗传算法 Genetic Algorithm」时会出现：

连续动作：

$a^{cont.}_i \subset \mathbb{R} \quad$

离散动作：

$a^{disc.} \in \mathbb{Z} \quad$

直接选择最大的数（锦标赛）：

$a^{disc.} = \arg \max(a^{cont.}_i) \quad$

按照概率随机选择（轮盘赌）：

$a^{disc} = RamdomChoiceByProb(a^{cont.}_i) \quad$

写成实际代码的时候，需要进行归一化处理与极小值处理，修改后的轮盘赌为：

a^{cont.}_i &= a^{cont.}_i - \min(a^{cont.}_i) + \epsilon

a^{cont.}_i &=a{cont.}_i\sum_{i=1}na^{cont.}_i \ a^{disc} &= RandomChoiceByProb(a^{cont.}_i)

其中，如果是 32 位浮点数（24 位数值），阿年 epsilon 取一个极小值为

$\epsilon = 0.00001$

= 0.00001 ；此外，

$\min(a^{cont.}_i) = -1.0$

。因而，代码中的相关函数为：

def adapt_action(action, action_max, action_dim, is_train):
    """
    action belongs to range(-1, 1), makes it suit for env.step(action)
    :return: state, reward, done, _
    """
    if action_max:  # action_space: Continuous
        return action * action_max
    else:  # action_space: Discrete
        if is_train:
            action_prob = action + 1.00001
            action_prob /= sum(action_prob)
            return rd.choice(action_dim, p=action_prob)
        else:
            return np.argmax(action)

5. 适应不同的游戏环境

让程序通过接口自行读取环境参数。例如：程序可以会自行向 gym 的环境确认动作空间的取值范围、数量、连续或者离散，然后自行去适应它，不需要手动修改：

env.make('ENV_NAME')

env.spec.reward_threshold # 通关目标，target_reward
env.observation_space.xxx # 状态空间，state
env.action_space.xxx      # 动作空间，action
...