密码学[1]：整数 模 多项式

1 整数

整数：没有小数的数字，用 Z 表示。

自然数：所有的正整数，用 N 表示。

实数：可用 n/m 表示，n ∈ Z，m ∈ N，用 Q 表示。

素数：对于自然数 p ∈ N，只可被自身和 1 整除，用 P 表示。

自然数的素数分解：每个自然数 n 都可分解为一系列素数，n = p1 · p2 · ... · pk

欧几里得除法：对于两个整数 a ∈ Z 和 b ∈ Z，且 b != 0，总是存在一个整数 m ∈ Z 和一个自然数 r ∈ N，0 ≤ r < |b|，使得 a = m · b + r，a 为被除数，b 为除数，m 是商，r 是余数。例如，−17 = −5 · 4 + 3

扩展的欧几里得算法：在计算两个自然数 a, b ∈ N 最大公约数（greatest common divisor）的同时，还能找到两个整数 s, t ∈ Z，使得 gcd(a, b) = s · a + t · b 成立。

扩展的欧几里得算法实现：

pub fn extended_euclidean(a: i32, b: i32) -> (i32, i32, i32) {
    if b == 0 {
        return (a, 1, 0);
    }

    let (d, mut t, s) = ext_euclidean(b, a % b);
    t -= a / b * s;
    return (d, s, t);
}

#[cfg(test)]
mod tests {
    use super::ext_euclidean;

    #[test]
    fn test_ext_euc() {
        let a = 6;
        let b = 8;
        let (d, s, t) = extended_euclidean(a, b);
        
        // [output] d: 2, s: -1, t: 1
        println!("d: {}, s: {}, t: {}", d, s, t);
        
        assert_eq!(a % d, 0);
        assert_eq!(b % d, 0);
        assert_eq!(d, s * a + t * b);
    }
}

两个整数互质：gcd(a, b) = 1

整数的表示：10 进制，2 进制（加上前缀 0b）、8 进制（加上前缀 0o）、16 进制（加上前缀 0x）

2 模

相似：两个整数 a, b ∈ Z 模一个自然数 n ∈ N, n >= 2 后相等，即 a mod n = b mod n，也可写作 a ≡ b ( mod n )

计算规则：

• 平移性：a1 ≡ b1 ( mod n ) ⇔ a1 + k ≡ b1 + k ( mod n )
• 缩放性：a1 ≡ b1 ( mod n ) ⇒ k · a1 ≡ k · b1 ( mod n )
• gcd(k, n) = 1 and k · a1 ≡ k · b1 ( mod n ) ⇒ a1 ≡ b1 ( mod n )
• k · a1 ≡ k · b1 ( mod k · n ) ⇒ a1 ≡ b1 ( mod n )
• 兼容加法：a1 ≡ b1 ( mod n ) 且 a2 ≡ b2 ( mod n ) ⇒ a1 + a2 ≡ b1 + b2 ( mod n )
• 兼容乘法：a1 ≡ b1 ( mod n ) 且 a2 ≡ b2 ( mod n ) ⇒ a1 ·a2 ≡ b1 ·b2 ( mod n )

费马小定理（Fermat's little theorem）：对于素数 p ∈ P 和整数 k ∈ Z, 有 k^p ≡ k ( mod p )。

所以，如果 k 和 p 互质，两边可同时除以 k，可得到 k^(p-1) ≡ 1 ( mod p )

中国余数定理（Chinese Remainder Theorem）：对于 k ∈ N 个互质的自然数 n1, n2, ..., nk ∈ N，以及任意的整数 a1, a2, ..., ak ∈ Z，下列一元线性同余方程组有解，且方程组任意两个解 x1, x2 模 N 同余，其中 N = n1 ·...· nk，即解的集合为 { x + m · N | m ∈ Z }

x ≡ a1 ( mod n1 )
x ≡ a2 ( mod n2 )
      ...
x ≡ ak ( mod nk )

中国余数定理实现：

pub fn chinese_remainder(n: Vec<i32>, a: Vec<i32>) -> (i32, i32) {
    assert_eq!(n.len(), a.len());

    let mut n_product = 1;
    for i in n.iter() {
        n_product *= *i;
    }

    let it = n.into_iter().zip(a.into_iter());
    let mut x = 0;

    for (ni, ai) in it {
        let nn = n_product / ni;
        let (_, s, _) = extended_euclidean(nn, ni);
        x += ai * s * nn;
        x %= n_product;
    }

    (x, n_product)
}

#[cfg(test)]
mod tests {
    use super::*;
    
	#[test]
    fn test_chinese_remainder() {
        let n: Vec<i32> = vec![7, 3, 5, 11];
        let a: Vec<i32> = vec![4, 1, 3, 0];
        let (x, n_product) = chinese_remainder(n, a);

        assert_eq!(x, 88);
        assert_eq!(n_product, 1155);
    }
}

余数类（remainder class or residue class）：模 n 后余数相等的一类数字。

余数类上的运算：假如 n = 6，2 + 5 = 8 + 11，因为 2 ≡ 8 ( mod 6 )，5 ≡ 11 ( mod 6 )

Z_6 表示余数为 6 的余数类及相关的运算。

模逆 Modular Inverses

一个整数在整数集 Z 上没有乘法逆，但是可能会在余数类 Z_6 上存在乘法逆。比如在 Z_6 上，5 · 5 = 1，所以 5 的乘法逆是 5。

对于模 n 运算 Z_n ，一个整数 r 是否有乘法逆，在于 n 和 r 是否互质。因为 gcd(n, r) = 1，根据扩展的欧几里得算法，存在 s, t ∈ Z，使得 1 = s · n + t · r 成立。如果该式子两边都模 n，那么 s · n 就会消失，即 1 = (t mod n) · r，所以 t mod n 就是 r 在 Z_n 上的乘法逆。

费马小定理提供了一种计算 Z_n 上的乘法逆的方法：对于素数 p 且 r < p，r^p ≡ r ( mod p ) ⇔ r^(p - 1) ≡ 1 ( mod p ) ⇔ r · r^( p- 2) ≡ 1 ( mod p ) ，所以 r 在模 p 运算 Z_p 上的乘法逆就是 r^(p-2)

3 多项式

主要系数（ leading coefficient）：多项式中最高度的系数。

零多项式（zero polynomial）：多项式的所有系数都是 0，即 p(x) = 0

一多项式（one polynomial）：多项式中只有常数 1，其它所有系数都是 0，即 p(x) = 1

整数多项式（Integer Polynomials）：多项式的系数必须都是整型，写作 Zx。

多项式长除法（Polynomial Long Division）：整数多项式 A(x) = x^5 + 2x^3 − 9 ∈ Zx 可被整数多项式 B(x) = x^2 + 4x − 1 ∈ Zx 整除。因为 B 不是零多项式，且主要系数是 1，在整数上拥有乘法逆，因此可以应用多项式欧几里得算法。

质因子分解（prime factors）：P = F1 · F2 · ... · Fk，其中，P 是多项式，F 是不可约多项式（类似于整数中的素数），被称为 P 的质因子（prime factor）

拉格朗日插值法（Lagrange Interpolation）：度为 m 的多项式可由 m + 1 个点唯一确定。当多项式的系数拥有乘法逆时，可用拉格朗日插值法根据 m + 1 个点计算出度为 m 的多项式：

例如，对于点集 S = {(0, 4), (-2, 1), (2, 3)}，可在实数域上计算出度为 2 的多项式：

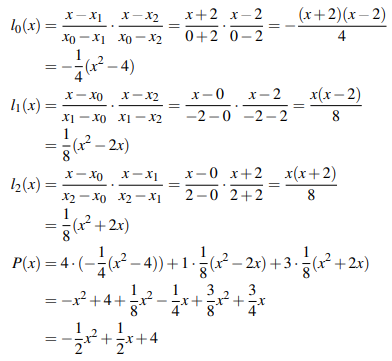
参考

The MoonMath Manual 第 3 章