数据结构与算法 | 二分搜索（Binary Search）

二分搜索（Binary Search）

文承上篇，搜索算法中除了深度优先搜索（DFS）和广度优先搜索（BFS），二分搜索（Binary Search）也是最基础搜索算法之一。

二分搜索也被称为折半搜索（Half-interval Search）也有说法为对数搜索算法（Logarithmic Search），用于在已排序的数据集中查找特定元素。

搜索过程从排序数据集的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束返回元素；如果某一特定元素大于或者小于中间元素，则在排序数据集中大于或小于中间元素的那一半中查找，继续重复开始的流程。反之亦然，如果在某一步骤排序数据集为空，则代表找不到。正如其名“二分”：每一次比较都使搜索范围缩小一半。

如果是对算法发展史有兴趣，二分搜索算法是算得上拥有一段悠长历史。最早可追溯到公元前200年的巴比伦尼亚中就有出现利用已排序的物件序列去加快搜索的构想，虽然该算法在计算机上的清楚描述出现在1946年约翰莫齐利（John Mauchly）的一篇文章里。

基本应用

二分搜索，最基本的应用就是查找特定元素。

LeetCode 35. 搜索插入位置【简单】

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。

使用递归进行编码逻辑也二分搜索常见的编程技巧之一，当然也并非一定要用递归的方式；不妨再练习一道题。

LeetCode 275. H指数 II 【中等】

给你一个整数数组 citations ，其中 citationsi 表示研究者的第 i 篇论文被引用的次数，citations 已经按照 升序排列 。计算并返回该研究者的 h 指数。 h 指数的定义：h 代表“高引用次数”（high citations），一名科研人员的 h 指数是指他（她）的 （n 篇论文中）总共有 h 篇论文分别被引用了至少 h 次。 请你设计并实现对数时间复杂度的算法解决此问题。

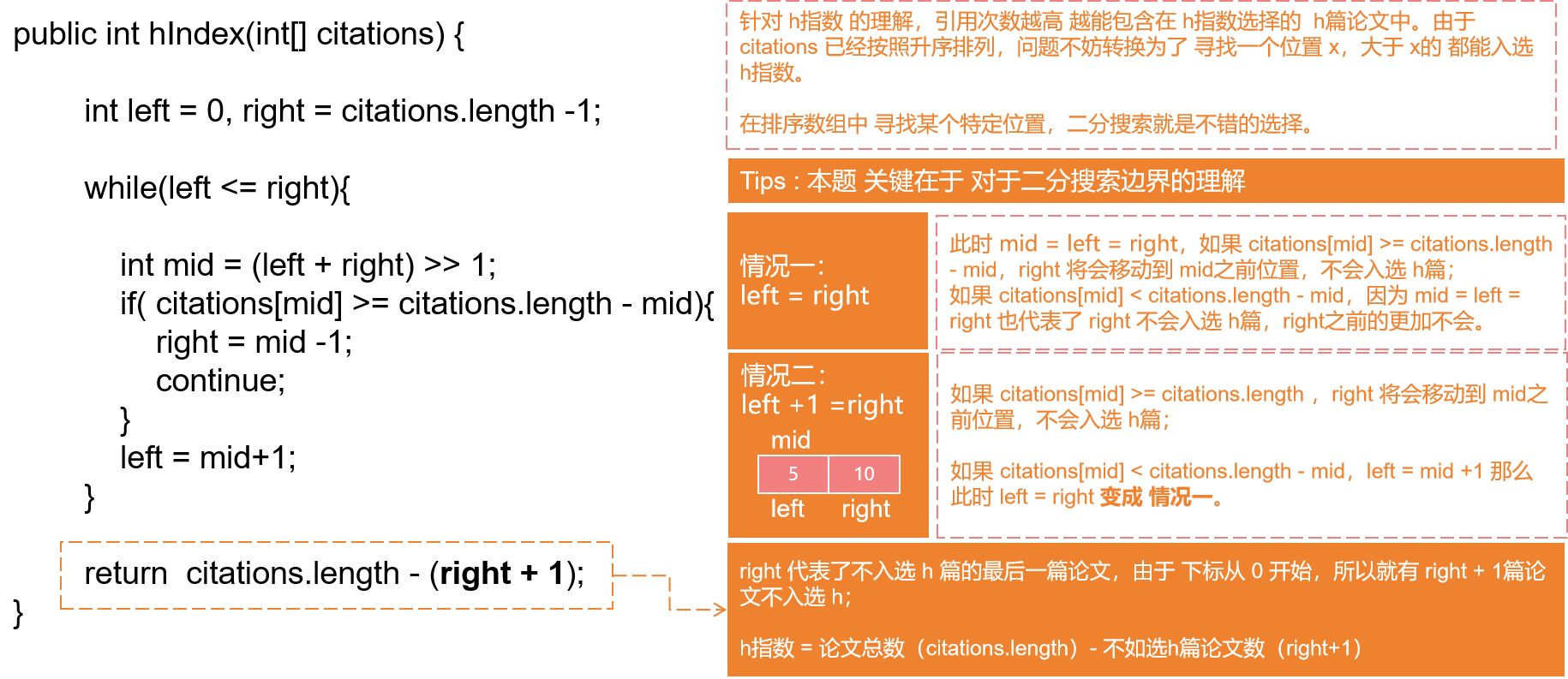
综合应用

对于问题解决往往可以有不同的算法思路来实现，对比来看或许更能感受到"二分"与"折半"的意义。不妨来一起感受下下面这题：

LeetCode 209. 长度最小的子数组【中等】

给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 numsl, numsl+1, ..., numsr-1, numsr ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

除开以上的解法，抛开使用前缀和的思路，也可以应用本系列第一篇数组中双指针的编程技巧来解。利用两个指针标识连续子数组的首位，再根据 总和 与 target之间的情况进行灵活调整指针也可以计算出最小长度；

在此不过多描述，附上代码：

public int minSubArrayLen(int target, int[] nums) {
        
        int left = 0,right = 0,sum = 0,min = Integer.MAX_VALUE;
        
        while(right < nums.length){
            sum += nums[right++];
            while (sum  >= target && left < right){
                min = Math.min(min,right - left);
                sum -= nums[left++];
            } 
        }
        
        return  min == Integer.MAX_VALUE ? 0:min;
    }

总结下

• 二分搜索是一种具有悠久历史的高效搜索算法，介绍基本算法流程；
• 透过算法问题进行了递归编码、递推编码以及使用JDK库函数实现二分搜索；
• 算法问题一般都有多种解法，通过对比更好理解二分的特性；

我正在参与2023腾讯技术创作特训营第三期有奖征文，组队打卡瓜分大奖！