半正矢公式（Haversine公式）
如果我们需要批量求两个已知经纬度的点之间的距离, 就会用到半正矢公式，本文记录公式内容和推导过程。
简介
半正矢公式是一种根据两点的经度和纬度来确定大圆上两点之间距离的计算方法，在导航有着重要地位。
hav 函数
定义 hav （半正失 Haversine 的缩写）函数：
这一步可以简单地通过半角公式推导得到
半正矢公式
对于任何球面上的两点，圆心角的半正矢值可以通过如下公式计算：
- {\displaystyle d} 是两点之间的距离（沿大圆，见球面距离）；
- {\displaystyle r} 是球的半径；
- {\displaystyle \varphi _{1}\varphi _{2}} ：点 1 的纬度和点 2 的纬度，以弧度制度量；
- {\displaystyle \lambda _{1}\lambda _{2}} ：点 1 的经度和点 2 的经度，以弧度制度量。
左边的等号 {\displaystyle {\frac {d}{r}}} 是圆心角，以弧度来度量。
：
其中
$$ \begin{aligned}\text{d}&=2r\arcsin\left(\sqrt{\mathrm{hav}(\varphi_2-\varphi_1)+\cos(\varphi_1)\cos(\varphi_2) \mathrm{hav}(\lambda_2-\lambda_1)}\right)\&=2r\arcsin\left(\sqrt{\sin^2\left(\frac{\varphi_2-\varphi_1}2\right)+\cos(\varphi_1)\cos(\varphi_2)\sin^2\left(\frac{\lambda_2-\lambda_1}2\right)}\right)\end{aligned} $$
误差说明
因为地球是一个不完美的球体，故当其应用于地球时，无论哪一个公式只是做一个近似测算，“地球半径” {\displaystyle R} 在极点地区是 {\displaystyle 6356.752} 公里，在赤道地区为 {\displaystyle 6378.137} 公里。另外，半径曲率在极点处（{\displaystyle \approx 6399.594} 公里）比在赤道处({\displaystyle \approx 6335.439} 公里)大 1% ，所以半正矢公式或者球面余弦定理是不能保证 0.5% 以内的误差。更准确的方法，应该是使用考虑地球离心率的 Vincenty 的公式或其他有关地理距离的论文所给出方法。
证明 1
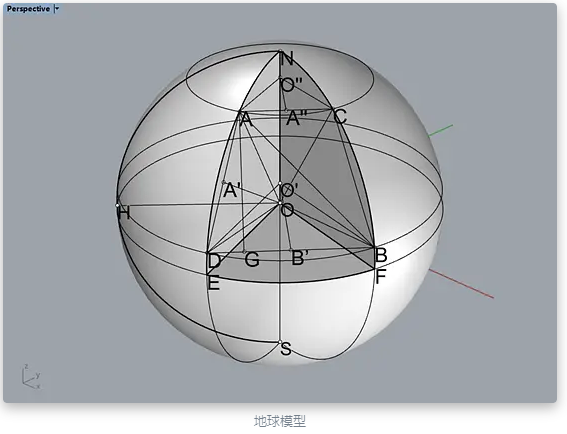
已知A(φ1，λ1)，B(φ2，λ2)，地球半径R。
在图中，A，B为地球表面已知经纬度的两点。N为北极点，S为南极点。弧NHS为本初子午线。弧HEF为赤道。弧NADES为经过A点的经线，弧AC为经过A点的纬线。弧NCBFS为经过B点的经线，弧DB为经过B点的纬线。
线段OA’是过O点的线段AD的垂线，又因为AO=DO，所以线段OA’是线段AD的中垂线；同理线段A’’O’’是线段AC的中垂线；线段B’O’是线段BD的中垂线。另，线段AG是过A点的线段BD的垂线，这根垂线是等腰梯形ACBD的高。
φ1=∠AOE=∠O’’AO，λ1=∠EOH，φ2=∠BOF=∠DOE=∠O’DO，λ2=∠FOH。
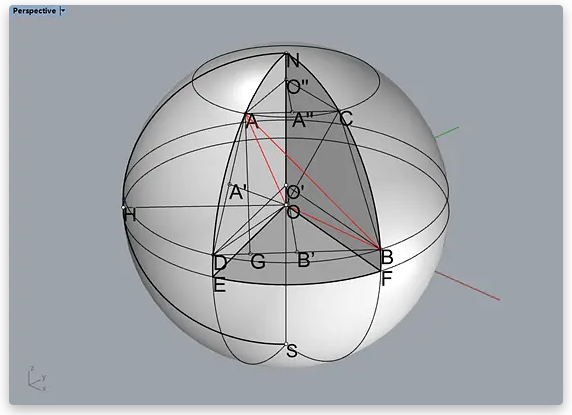
这个算法的思路，是计算线段AB的长度LAB，再结合线段AO和BO的长度都等于地球半径R，可以反向计算∠AOB的大小，并计算出弧AB的长度。
加一句题外话，在AB距离较小，∠AOB趋近于零的时候，弧AB的长度近似等于线段AB也不是不可以。
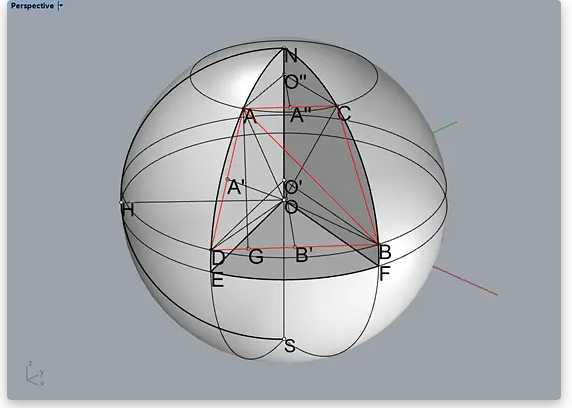
为了计算线段AB的长度LAB，就得借助一套辅助线，就是等腰梯形ACBD，线段AB是等腰梯形ACBD的对角线。
而用一系列的三角函数和勾股定理，可以根据A、B点的坐标计算出线段AD、BD、AC、BC的长度，其中AD=BC。
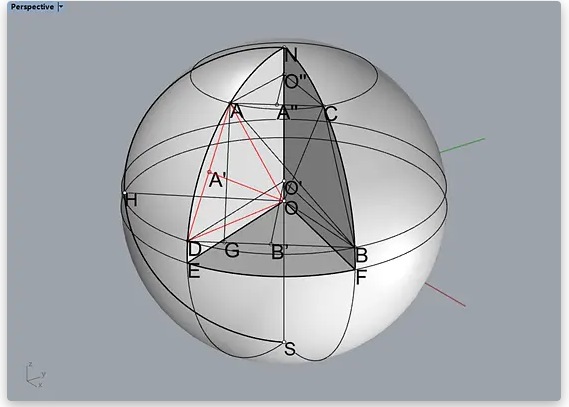
先求线段AD也就是线段BC的长度LAD，这里是用三角函数来求的。
∠AOE=φ1，∠DOE=∠BOF=φ2。
所以∠AOD=(φ1-φ2)。因为OA’是线段AD的中垂线，所以∠AOA’=∠AOD/2。LAA’=R_Sin(∠AOA’)=R_Sin(∠AOD/2)=R*Sin((φ1-φ2)/2)。
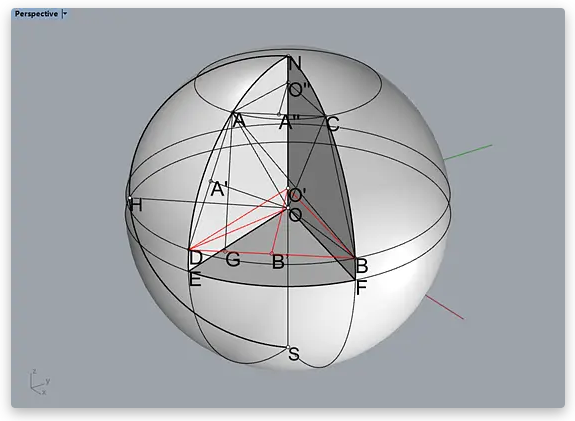
这里关于∠DO’B要多说一句：因为弧NAEDS和弧NCDFS都是经线，而NS是穿南北极的地轴，所以∠DO’B=∠EOF=∠AO’’C=λ2-λ1。
那么先算线段DO’的长度LDO’，LDO’=R_Cos(∠DOE)=R_Cos(φ2)。
结合以上两步，得出 L_{BD}=2R\cos(φ_2)\sin((λ_2-λ_1)/2) .
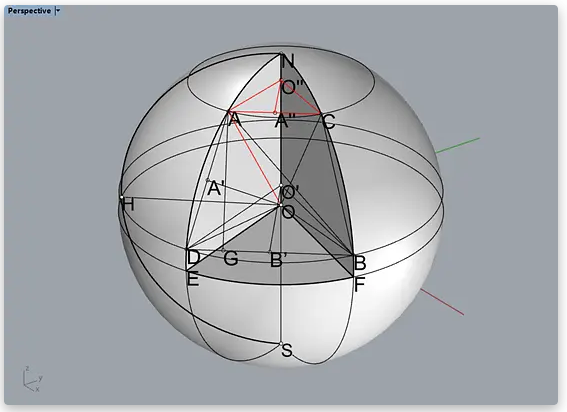
这时再来求线段AC的长度LAC，思路和求LBD是一模一样的，就不再写一遍了。
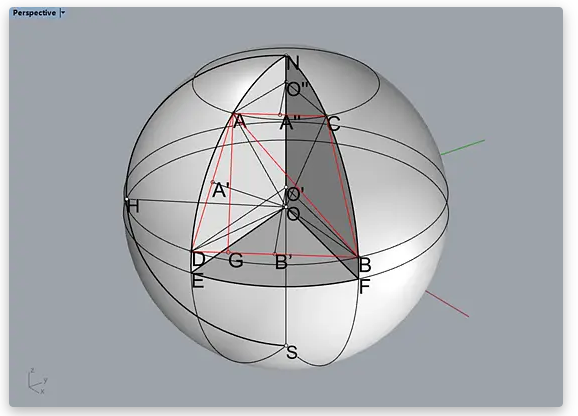
经过前面的一系列计算，已经得出了以下数据：
一个已知四条边长度的等腰梯形的对角线长度，应该有非常成熟的公式，但既然来写笔记，就一并过一遍。
先算线段AG的长度L_{AG} ，而要算L_{AG} ，就在直角三角形ADG里面用勾股定理， L_{AG}^2=L_{AD}^2-L_{DG}^2 。那就得先算线段DG的长度L_{DG} ，L_{DG}=(L_{DB}-L_{AC})/2 。
于是:
$$ L_{AG}^2=(2R\sin((φ_1-φ_2)/2))^2-(R(\cos(φ_2)-\cos(φ_1))\sin((λ_2-λ_1)/2)^2 $$
这里就先不忙开方了，因为为了算线段AB的长度LAB，又会用到一个勾股定理，L_{AB}2=L_{AG}2+L_{BG}^2 。
先线段BG的长度，L_{BG}=L_{BD}-L_{DG}=(L_{DB}+L_{AC})/2 ，把这个带进上面的勾股定理里面，就可以得到：
$$ \begin{array}{l} L_{AB}^2&=&(2R\sin((φ_1-φ_2)/2))^2-(R(\cos(φ_2)-\cos(φ_1))\sin((λ_2-λ_1)/2)^2+(R(\cos(φ_2)+C\cos(φ_1))*\sin((λ_2-λ_1)/2)^2\ &=&4R^2(\sin((φ_1-φ_2)/2)^2+\cos(φ_1)\cos(φ_2)\sin((λ_2-λ_1)/2)) \end{array} $$ $$ L_{AB}=2R(\sin ((φ_1-φ_2)/2)^2+\cos(φ_1)\cos(φ_2)(\sin((λ_2-λ_1)/2))^2)^{0.5} $$
证明 2
取单位球上a、b两点对应A、B，（坐标系绕南北极旋转后）令点a经度为0、点b经度为λ≡λ₂－λ₁，两点纬度保持φ₁和φ₂不变。
向量 Oa≡(cos(φ₁), 0, sin(φ₁))
代入 haversine 函数可知上述结果与半正矢公式等价。