正式宣战，DeepSeek 顶得住吗？

宫水三叶的刷题日记

发布于 2025-02-05 16:34:15

1750

文章被收录于专栏：宫水三叶的刷题日记宫水三叶的刷题日记

写在前面

DeepSeek

DeepSeek 火了，昨天聊到 DeepSeek 这家公司的薪资水平的时候，还有不少读者表示没听过，今天再来给大家好好介绍一下。

要是大家对 DeepSeek 的出圈程度还没概念的话，我举个例子，或许大家就理解了。

连创始人回家过年，都能上热搜第四：

这可是顶流雷军都没有的待遇啊？！🤣🤣🤣

好了，言归正传。

DeepSeek 的母公司是国内头部量化对冲基金「幻方量化」，是一家百亿规模的私募机构。

DeepSeek 如此强大，要是和母公司的量化模型稍稍结合，那么收割散户是秒秒钟（不是分分钟，量化没这么慢）的事儿。

虽然幻方量化曾公开表示并未将 DeepSeek 和量化交易程序结合，但冥冥中，我仍然觉得活跃在 A 股市场的我，对 DeepSeek 尽过不少"捐献"的义务

这几天看了不少关于 DeepSeek 的新闻，印象最深刻的，是一位曾经面试过 DeepSeek 的应届生该公司的评价。

❝“只招 1% 的天才，去做 99% 中国公司做不到的事情。” ❞

某种程度上 DeepSeek 确实和早期的 OpenAI 很像，二者都更像是纯粹的研究机构（不融资，不考虑商业化）。

但随着 ChatGPT 的爆火，OpenAI 很多决定都开始往"如何实现盈利最大化"的方向去考虑，而非单纯的技术本身。再后来甚至一度上演「创始人退出，CEO 出走」等宫斗剧情，之后还被马斯克讽刺其为"ClosedAI"。

DeepSeek-R1 的出现，一定程度打击了这些"只搞闭源，藏着掖着，想靠自己手上领先一步的 AI 模型大赚一笔"的公司。

就在刚刚，Open AI 的创始人兼 CEO 正式对回应了 DeepSeek：

奥特曼表示：DeepSeek-R1 确实让人眼前一亮，尤其是在成本方面。但 OpenAI 很快就会提供更好的模型，有了像 DeepSeek 这样的对手，让他们感到兴奋，承诺很快会发布新的产品。

这一定程度也算是正式宣战了。

这也是科技领域真正有趣的地方，不会有"百年企业"，所谓的技术护城河可能会在一夜间坍塌，"以下犯上"式的超越基本上每天都会发生。

今天你领先我，明天就不一定了。

对此，你怎么看？你觉得 OpenAI 还能稳坐行业头把交椅，发布领先时代的新模型吗？还是由 DeepSeek 作为开端，百花齐放的时代将要到来？欢迎评论区交流。

...

回归主题。

大年初一，来一道简单算法题。

题目描述

平台：LeetCode

题号：661

图像平滑器是大小为

3 \times 3

的过滤器，用于对图像的每个单元格平滑处理，平滑处理后单元格的值为该单元格的平均灰度。

每个单元格的平均灰度定义为：该单元格自身及其周围的

个单元格的平均值，结果需向下取整（即需要计算蓝色平滑器中

个单元格的平均值）。

如果一个单元格周围存在单元格缺失的情况，则计算平均灰度时不考虑缺失的单元格（即，需要计算红色平滑器中

个单元格的平均值）。

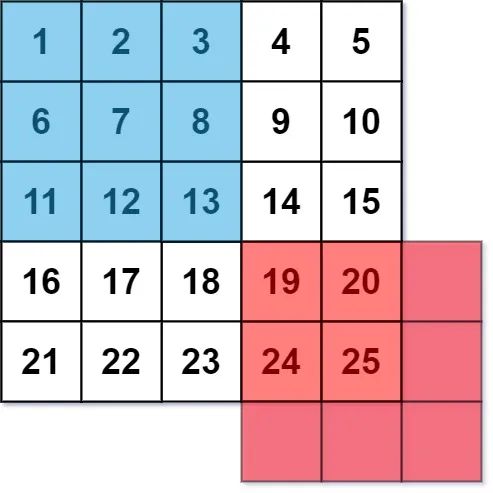
给你一个表示图像灰度的

m \times n

整数矩阵 img ，返回对图像的每个单元格平滑处理后的图像。

示例 1:

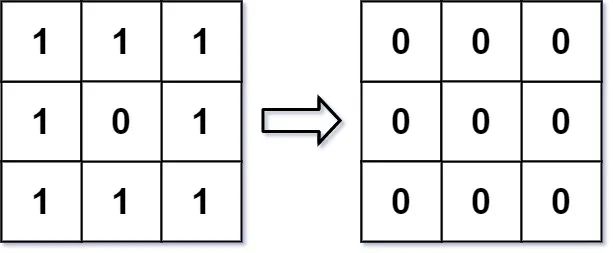
输入:img = [[1,1,1],[1,0,1],[1,1,1]]

输出:[[0, 0, 0],[0, 0, 0], [0, 0, 0]]

解释:
对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0
对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0
对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0

示例 2:

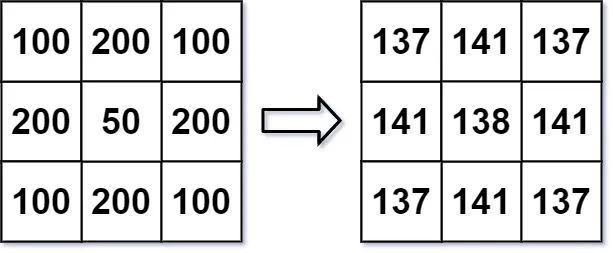
输入: img = [[100,200,100],[200,50,200],[100,200,100]]

输出: [[137,141,137],[141,138,141],[137,141,137]]

解释:
对于点 (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
对于点 (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
对于点 (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138

提示:

m = img.length

n = img[i].length

1 <= m, n <= 200

0 <= img[i][j] <= 255

模拟

为了方便，我们称每个单元格及其八连通方向单元格所组成的连通块为一个 item。

数据范围只有

200

，我们可以直接对每个 item 进行遍历模拟。

Java 代码：

class Solution {
    public int[][] imageSmoother(int[][] img) {
        int m = img.length, n = img[0].length;
        int[][] ans = new int[m][n];
        int[][] dirs = new int[][]{{0,0},{1,0},{-1,0},{0,1},{0,-1},{-1,-1},{-1,1},{1,-1},{1,1}};
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int tot = 0, cnt = 0;
                for (int[] di : dirs) {
                    int nx = i + di[0], ny = j + di[1];
                    if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
                    tot += img[nx][ny]; cnt++;
                }
                ans[i][j] = tot / cnt;
            }
        }
        return ans;
    }
}

C++ 代码：

class Solution {
public:
    vector<vector<int>> imageSmoother(vector<vector<int>>& img) {
        int m = img.size();
        if (m == 0) return {};
        int n = img[0].size();
        vector<vector<int>> ans(m, vector<int>(n, 0));
        vector<vector<int>> dirs = {{0, 0}, {1, 0}, {-1, 0}, {0, 1}, {0, -1}, {-1, -1}, {-1, 1}, {1, -1}, {1, 1}};
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int tot = 0, cnt = 0;
                for (const auto& di : dirs) {
                    int nx = i + di[0], ny = j + di[1];
                    if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
                    tot += img[nx][ny]; cnt++;
                }
                ans[i][j] = tot / cnt;
            }
        }
        return ans;
    }
};

Python 代码：

dirs = list(product(*[[-1,0,1]] * 2))
class Solution:
    def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:
        m, n = len(img), len(img[0])
        ans = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                tot, cnt = 0, 0
                for di in dirs:
                    if 0 <= (nx := i + di[0]) < m and 0 <= (ny := j + di[1]) < n:
                        tot += img[nx][ny]
                        cnt += 1
                ans[i][j] = tot // cnt
        return ans

TypeScript 代码：

function imageSmoother(img: number[][]): number[][] {
    const m = img.length;
    if (m === 0) return [];
    const n = img[0].length;
    const ans = new Array(m).fill(0).map(() => new Array(n).fill(0));
    const dirs = [[0, 0], [1, 0], [-1, 0], [0, 1], [0, -1], [-1, -1], [-1, 1], [1, -1], [1, 1]];
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            let tot = 0, cnt = 0;
            for (const di of dirs) {
                const nx = i + di[0], ny = j + di[1];
                if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
                tot += img[nx][ny]; cnt++;
            }
            ans[i][j] = Math.floor(tot / cnt);
        }
    }
    return ans;
};

时间复杂度：

O(m \times n \times C)

，其中

为灰度单位所包含的单元格数量，固定为

空间复杂度：

O(m \times n)

前缀和

在朴素解法中，对于每个

ans[i][j]

我们都不可避免的遍历

联通方向，而利用「前缀和」我们可以对该操作进行优化。

对于某个

ans[i][j]

而言，我们可以直接计算出其所在 item 的左上角

(a, b) = (i - 1, j - 1)

以及其右下角

(c, d) = (i + 1, j + 1)

，同时为了防止超出原矩阵，我们需要将

(a, b)

与

(c, d)

对边界分别取 max 和 min。

当有了合法的

(a, b)

和

(c, d)

后，我们可以直接计算出 item 的单元格数量（所包含的行列乘积）及 item 的单元格之和（前缀和查询），从而算得

ans[i][j]

。

Java 代码：

class Solution {
    public int[][] imageSmoother(int[][] img) {
        int m = img.length, n = img[0].length;
        int[][] sum = new int[m + 10][n + 10];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + img[i - 1][j - 1];
            }
        }
        int[][] ans = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int a = Math.max(0, i - 1), b = Math.max(0, j - 1);
                int c = Math.min(m - 1, i + 1), d = Math.min(n - 1, j + 1);
                int cnt = (c - a + 1) * (d - b + 1);
                int tot = sum[c + 1][d + 1] - sum[a][d + 1] - sum[c + 1][b] + sum[a][b];
                ans[i][j] = tot / cnt;
            }
        }
        return ans;
    }
}

C++ 代码：

class Solution {
public:
    vector<vector<int>> imageSmoother(vector<vector<int>>& img) {
        int m = img.size(), n = img[0].size();
        vector<vector<int>> sumv(m + 2, vector<int>(n + 2, 0));
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                sumv[i][j] = sumv[i - 1][j] + sumv[i][j - 1] - sumv[i - 1][j - 1] + img[i - 1][j - 1];
            }
        }
        vector<vector<int>> ans(m, vector<int>(n, 0));
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int a = max(0, i - 1), b = max(0, j - 1);
                int c = min(m - 1, i + 1), d = min(n - 1, j + 1);
                int cnt = (c - a + 1) * (d - b + 1);
                int tot = sumv[c + 1][d + 1] - sumv[a][d + 1] - sumv[c + 1][b] + sumv[a][b];
                ans[i][j] = tot / cnt;
            }
        }
        return ans;
    }
};

Python 代码：

class Solution:
    def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:
        m, n = len(img), len(img[0])
        sum = [[0] * (n + 10) for _ in range(m + 10)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + img[i - 1][j - 1]
        ans = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                a, b = max(0, i - 1), max(0, j - 1)
                c, d = min(m - 1, i + 1), min(n - 1, j + 1)
                cnt = (c - a + 1) * (d - b + 1)
                tot = sum[c + 1][d + 1] - sum[a][d + 1] - sum[c + 1][b] + sum[a][b]
                ans[i][j] = tot // cnt
        return ans

TypeScript 代码：

function imageSmoother(img: number[][]): number[][] {
    const m = img.length, n = img[0].length;
    const sum = Array.from({ length: m + 10 }, () => new Array(n + 10).fill(0));
    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + img[i - 1][j - 1];
        }
    }
    const ans = Array.from({ length: m }, () => new Array(n).fill(0));
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            const a = Math.max(0, i - 1), b = Math.max(0, j - 1);
            const c = Math.min(m - 1, i + 1), d = Math.min(n - 1, j + 1);
            const cnt = (c - a + 1) * (d - b + 1);
            const tot = sum[c + 1][d + 1] - sum[a][d + 1] - sum[c + 1][b] + sum[a][b];
            ans[i][j] = Math.floor(tot / cnt);
        }
    }
    return ans;
};