《机器学习核心算法》六、决策树-信息熵与信息增益计算

大家好！今天我们来聊聊决策树-信息熵与信息增益计算，这是一种非常直观且强大的机器学习算法。想象一下，你正在玩一个“二十问”游戏，通过一系列问题来猜出对方心里想的东西。决策树的工作方式与之类似，它通过一系列的决策规则，将数据逐步划分到不同的类别中。决策树在医疗诊断、金融风险评估等领域都有广泛应用，因为它不仅能做出预测，还能清晰地展示决策过程。

一、决策树的基本结构

决策树由节点和分支组成。每个内部节点代表一个特征属性上的判断，比如“年龄是否大于30岁？”。每个分支代表一个判断结果，比如“是”或“否”。最终，每个叶节点代表一个类别标签或一个连续值，也就是我们的预测结果。简单来说，决策树就像一棵倒立的树，从根节点开始，沿着分支向下，最终到达叶节点。

决策树的构建过程

假设我们要判断一个人是否适合户外运动，我们的决策树会考虑天气和温度这两个因素。

1. 根节点：从最重要的特征开始，比如“天气是否晴朗？”。
2. 分支：根据天气的判断结果，分为“晴朗”和“非晴朗”两个分支。
3. 叶节点：如果天气晴朗，进一步检查温度是否适宜。如果温度适宜，则判断为“适合户外运动”；否则判断为“不适合户外运动”。

这种透明的决策过程使得决策树在需要解释模型决策的关键领域非常受欢迎。

二、信息熵的概念

现在，我们来了解一个重要的概念：信息熵。信息熵用来衡量随机变量的不确定性。熵越高，数据越混乱；熵越低，数据越纯净。举个例子，如果一个盒子里面全是红球，那么它的熵为0，因为没有不确定性。如果一个盒子里面红球和蓝球各一半，那么它的熵就比较高，因为我们无法确定下次摸出的是什么颜色的球。

信息熵的计算公式

示例计算

假设我们有一个硬币，正面和反面出现的概率都是 0.5。那么它的信息熵为：

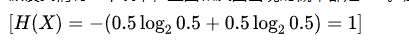
这意味着当两个事件的概率相等时，系统的不确定性最大，信息熵也最大。

三、信息增益的定义

接下来，我们来学习信息增益。信息增益是指通过某个特征进行分裂后，数据集纯度的提升程度。简单来说，就是看使用哪个特征来划分数据，能让数据变得更“纯净”。信息增益越大，表示该特征对于分类的贡献越大，我们就应该优先选择这个特征来构建决策树。

信息增益的计算公式

示例计算

四、ID3 算法：使用信息增益选择特征

ID3 算法是决策树构建的经典算法之一，它使用信息增益作为选择特征的准则。ID3 算法会计算每个特征的信息增益，然后选择信息增益最大的特征来划分数据。这个过程会递归地进行下去，直到所有数据都被划分到同一个类别，或者没有更多的特征可以用来划分数据。

ID3 算法的步骤

1. 计算所有特征的信息增益。
2. 选择信息增益最大的特征作为当前节点的分裂特征。
3. 对每个子集递归执行相同的过程。
4. 满足停止条件时，将当前节点设为叶节点。

示例

假设我们有一个关于天气和出门决策的数据集，包含天气、温度、湿度、风力四个特征，目标是预测是否适合运动。

1. 计算每个特征的信息增益：
   • 天气：0.421
   • 温度：0.247
   • 湿度：0.152
   • 风力：0.048
2. 选择信息增益最大的特征：
   • 选择“天气”作为根节点的分裂特征。
3. 递归构建决策树：
   • 晴天子集：继续选择“风力”作为分裂特征。
   • 阴天子集：全部是“是”，成为叶节点。
   • 雨天子集：继续选择“风力”作为分裂特征。
4. 停止条件：
   • 当前节点的所有样本都属于同一类别。
   • 没有更多特征可用于划分。
   • 样本数量太少。

ID3 算法具有算法简单、易于理解的优点，生成的决策树具有良好的可解释性。但它也有一些局限性，比如偏向于选择取值较多的特征，无法直接处理连续型特征，容易产生过拟合等问题。

五、C4.5 算法：使用信息增益比改进 ID3

C4.5 算法是 ID3 算法的改进版本。ID3 算法有一个缺点，就是它偏向于选择取值数目较多的特征。为了克服这个缺点，C4.5 算法使用信息增益比来选择特征。信息增益比是对信息增益进行归一化处理后的结果，它可以有效地避免选择取值数目较多的特征。

示例计算

六、CART 算法：使用基尼系数进行特征选择

CART 算法是另一种常用的决策树算法，它使用基尼系数作为选择特征的准则。基尼系数衡量随机选择的属性被错误分类的频率。基尼系数越小，表示数据集的纯度越高。CART 算法会选择基尼系数最小的特征来划分数据。

七、信息熵与基尼系数的比较

信息熵和基尼系数都是用来衡量数据集纯度的指标。在数据维度较低、数据比较清晰的情况下，信息熵和基尼系数没有太大的区别。但是在处理数据维度很大、噪音很大的数据时，基尼系数通常表现更好。

信息熵与基尼系数的对比

• 信息熵：计算复杂度较高，但在清晰数据上表现好。
• 基尼系数：计算简单，且在噪音数据上更鲁棒。

选择使用哪个指标主要取决于你的数据特征。理解这一点将帮助你在实际应用中做出更好的决策。

八、决策树的剪枝：防止过拟合

决策树很容易过拟合，也就是说，它在训练数据上表现很好，但在测试数据上表现很差。为了防止过拟合，我们需要对决策树进行剪枝。剪枝有两种方法：预剪枝和后剪枝。预剪枝是在决策树构建过程中进行剪枝，比如限制树的深度或叶节点的最小样本数。后剪枝是在决策树构建完成后进行剪枝，比如通过交叉验证来评估每个节点的重要性，然后删除不重要的节点。

预剪枝与后剪枝

• 预剪枝：在构建决策树的过程中进行剪枝，比如限制树的深度或叶节点的最小样本数。
• 后剪枝：在决策树构建完成后进行剪枝，通过评估每个节点的重要性来删除不重要的节点。

剪枝的效果非常明显。通过合理的剪枝，我们可以显著提高模型在测试数据上的表现，让决策树既准确又实用。

九、集成学习：提升决策树的性能

为了进一步提升决策树的性能，我们可以使用集成学习方法。集成学习是将多个弱学习器组合成一个强学习器的方法。常用的决策树集成学习方法包括随机森林和梯度提升树。随机森林通过随机选择特征和样本来构建多个决策树，然后对这些决策树的预测结果进行平均或投票。梯度提升树通过迭代地训练多个决策树，每个决策树都试图纠正前一个决策树的错误。

随机森林与梯度提升树

• 随机森林：通过随机选择特征和样本来构建多个决策树，然后对这些决策树的预测结果进行平均或投票。
• 梯度提升树：通过迭代地训练多个决策树，每个决策树都试图纠正前一个决策树的错误。

随机森林和梯度提升树都是强大的集成学习方法，可以显著提升决策树的性能。

十、随机森林：多个决策树的组合

随机森林是一种非常流行的集成学习算法，它由多个决策树组成。随机森林通过随机选择特征和样本来构建多个决策树，这使得随机森林具有很强的泛化能力，不容易过拟合。随机森林的预测结果是通过对所有决策树的预测结果进行平均或投票得到的。

随机森林的工作原理

1. 随机选择特征和样本：从原始数据集中随机选择特征和样本，构建多个不同的决策树。
2. 构建决策树：使用每个子集构建一个决策树。
3. 预测结果：对所有决策树的预测结果进行平均或投票，得到最终的预测结果。

随机森林具有许多优势：它能有效减少过拟合风险，提高模型的泛化能力，对噪声数据具有很好的鲁棒性，还能处理缺失值并提供特征重要性信息。这些特点使得随机森林成为实际应用中非常受欢迎的算法。

十一、梯度提升树：迭代地提升性能

梯度提升树是另一种常用的集成学习算法。梯度提升树通过迭代地训练多个决策树，每个决策树都试图纠正前一个决策树的错误。梯度提升树的预测结果是通过将所有决策树的预测结果加权求和得到的。梯度提升树通常比随机森林具有更高的预测准确性，但也更容易过拟合。

梯度提升树的工作原理

1. 初始化：从一个简单的决策树开始，比如一个常数树。
2. 迭代训练：在每次迭代中，计算当前模型的残差，训练一个新的决策树来拟合这些残差。
3. 更新模型：将新训练的决策树加到当前模型中，更新模型的预测结果。
4. 重复迭代：重复上述过程，直到达到预定的迭代次数或模型收敛。

梯度提升树通过逐步纠正错误，逐步提升模型的性能。它通常能达到更高的预测准确性，但也需要注意过拟合的问题。

十二、决策树的可解释性

决策树最大的优点之一就是它的可解释性。决策树的决策过程非常直观，我们可以很容易地理解决策树是如何做出预测的。这使得决策树在需要解释模型决策过程的领域非常受欢迎，比如医疗诊断和金融风险评估。

决策树在医疗诊断中的应用

在医疗诊断中，决策树可以根据病人的症状和检查结果，构建决策树模型来辅助医生进行诊断。例如，我们可以构建一个决策树来判断病人是否患有糖尿病，这个决策树会根据病人的血糖水平、年龄、体重等特征来进行判断。决策树的可解释性使得医生可以理解模型是如何做出诊断的，从而更好地信任模型。

决策树在客户流失预测中的应用

企业可以利用决策树分析客户行为模式，预测哪些客户可能流失，并采取相应措施。例如，我们可以构建一个决策树来预测客户是否会取消订阅服务，这个决策树会根据客户的消费记录、登录频率、投诉次数等特征来进行判断。通过预测客户流失，企业可以提前采取措施，挽留潜在的流失客户。

决策树在金融风险评估中的应用

银行可以使用决策树来评估贷款申请人的信用风险。例如，我们可以构建一个决策树来判断贷款申请人是否会违约，这个决策树会根据贷款申请人的收入、信用记录、工作年限等特征来进行判断。通过评估信用风险，银行可以更好地控制贷款风险。

决策树在问卷调查中的应用

在问卷调查中，我们可以通过信息熵和信息增益选择区分能力最强的问题，设计更简短的问卷。例如，我们可以先收集一些候选问题，然后计算每个问题的信息增益，选择信息增益最大的问题作为问卷的第一个问题。然后，我们可以根据第一个问题的答案，再次计算剩余问题的信息增益，选择信息增益最大的问题作为问卷的第二个问题。这个过程会一直进行下去，直到我们得到一个足够短且区分能力强的问卷。

十三、决策树的未来发展趋势

决策树算法仍然是机器学习领域中一个活跃的研究方向。未来，决策树将更多地与其他算法结合，构建更强大的模型，如随机森林、梯度提升树等。同时，决策树将更多地应用于需要解释模型决策过程的领域，例如医疗诊断、金融风险评估等。此外，研究人员还将继续研究如何利用决策树处理高维数据、缺失数据和非线性数据，以及如何将决策树应用于在线学习场景。

决策树处理复杂数据的挑战

虽然决策树有很多优点，但也面临着一些挑战。例如，决策树在处理高维数据时容易过拟合，因为高维数据包含大量的噪声。此外，决策树在处理缺失数据时也比较困难，因为缺失数据会导致信息熵的计算不准确。最后，决策树在处理非线性数据时表现不佳，因为决策树只能进行线性划分。

决策树的在线学习应用

在线学习是指模型能够适应不断变化的数据流。决策树可以应用于在线学习场景，使其能够适应不断变化的数据流。例如，我们可以使用一种称为“Hoeffding树”的决策树算法来进行在线学习。Hoeffding树会根据数据流中的样本逐步构建决策树，并在每次接收到新的样本时更新树的结构。

十四、总结与展望

今天我们学习了决策树的基本概念、信息熵和信息增益的计算方法，以及决策树在各个领域的应用。决策树是一种非常强大且易于理解的机器学习算法，它在医疗诊断、金融风险评估等领域都有广泛应用。未来，随着研究的不断深入，决策树将在更多领域发挥重要作用。