【优选算法必刷100题】第003~004题（双指针算法）：快乐数、盛最多水的容器问题求解

003 快乐数

力扣链接：202. 快乐数

力扣题解链接：快慢双指针、鸽巢原理解决【快乐数】

题目描述：

1.1 题目分析与简单证明

1.1.1 题目分析

为了方便叙述，将【对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和】这个操作记为 x 操作；题目告诉我们，当我们不断重复 x 操作的时候，计算一定会【死循环】，这个【死循环】有两种“死法”：

情况一：一直在 1 中死循环，即1 -> 1 -> 1 -> 1…… 情况二：在历史的数据中死循环，但始终变不到1

由于以上两种情况只会出现一种，因此，只要我们能确定循环是在【情况一】中进行，还是在【情况二】中进行，就能得到结果。

1.1.2 简单证明

（1）经过一次变化之后的最大值 9 ^ 2 * 10 = 810（2 ^ 31 - 1 = 2147483647。选一个更大的，最大9999999999），也就是变化的区间在[1 , 810]之间； （2）根据【鸽巢原理】，一个数变化811次之后，必然会形成一个循环； （3）因此，变化的过程最终会走到一个圈里面，因此可以用【快慢指针】来解决。

1.2 思路

双指针算法——

用快慢指针解决。 1、定义快慢指针； 2、慢指针每次向后移动一步，快指针每次向后移动两步； 3、判断相遇时候的值即可

1.3 算法流程

我们的思路：根据上面的题目分析，我们可以知道，当重复执行x的时候，数据会陷入到一个【循环】之中。而【快慢指针】有一个特性，就是在一个圆圈中，快指针总是会追上慢指针，即它们总是会相遇在一个位置上。如果相遇位置的值是1，那么这个数一定是快乐数；如果相遇位置不是1的话，那就不是快乐数。

补充知识：如何求一个数n在每个位置上的平方和。

1、把数 n 每一位的数提取出来——

循环迭代下面步骤：

（1）提取个位

int t = n % 10;

（2）干掉个位

n /= 10;

直到 n 的值变为0。

2、提取每一位的时候，用一个变量tmp来记录这一位的平方与之前提取位数的平方和

tmp = tmp + t * t;

1.4 代码实现

代码演示：

class Solution {
public:
    int bitSum(int n)
    {
        int sum = 0;
        while(n)
        {
            int t = n % 10;
            sum += t * t;
            n /= 10;
        }
        return sum;
    }
    bool isHappy(int n) {
        int slow = n,fast = bitSum(n);
        while(slow != fast)
        {
            slow = bitSum(slow);
            fast = bitSum(bitSum(fast));
        }
        return slow == 1;
    }
};

时间复杂度：O(N)，空间复杂度：O(1)。

1.5 过程推算

本题整个的思路、算法原理、解题过程博主在纸上推导了一遍，大家可以参考一下！

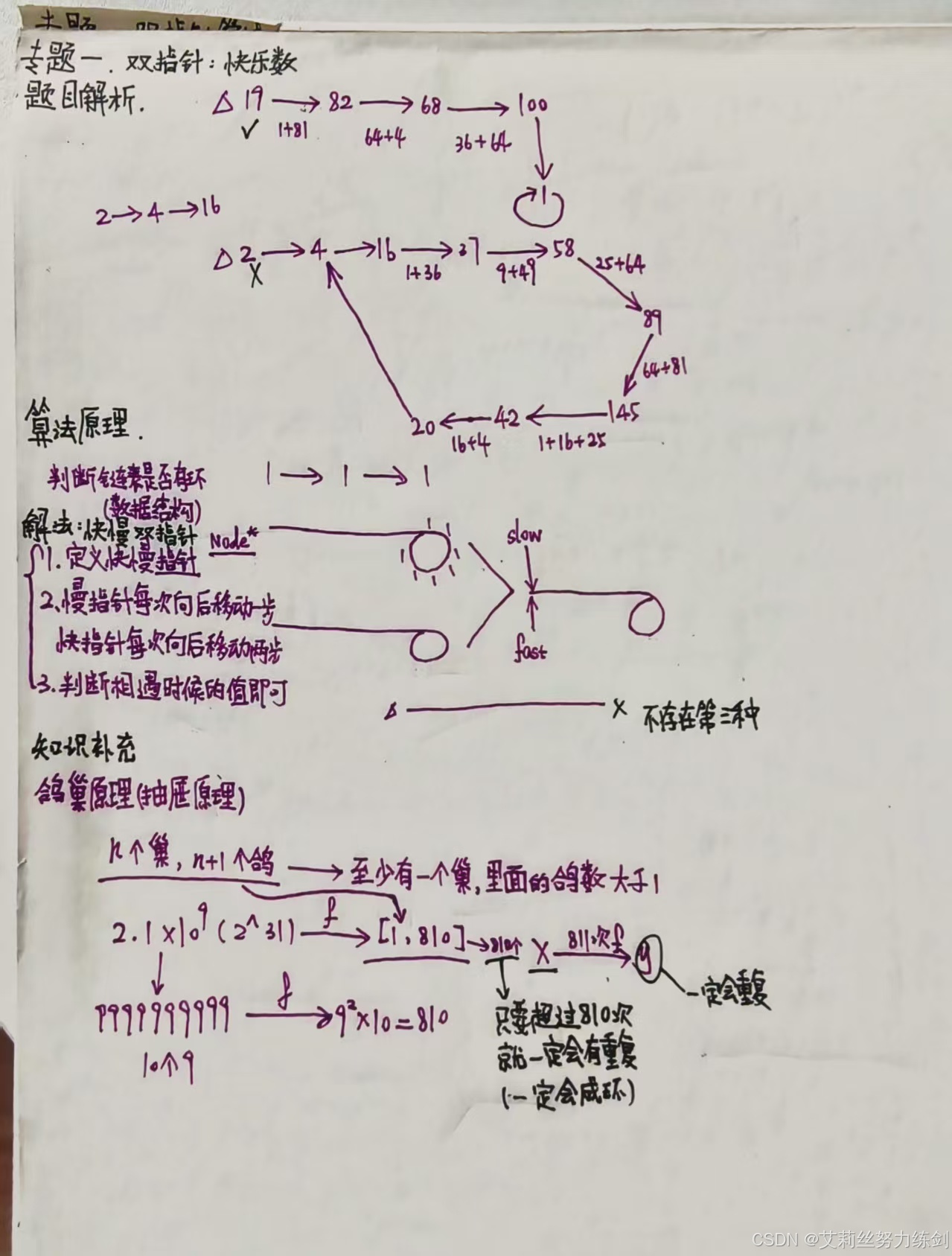
004 盛最多水的容器

力扣链接：11. 盛最多水的容器

力扣题解链接：双指针解决【盛最多水的容器】问题

题目描述：

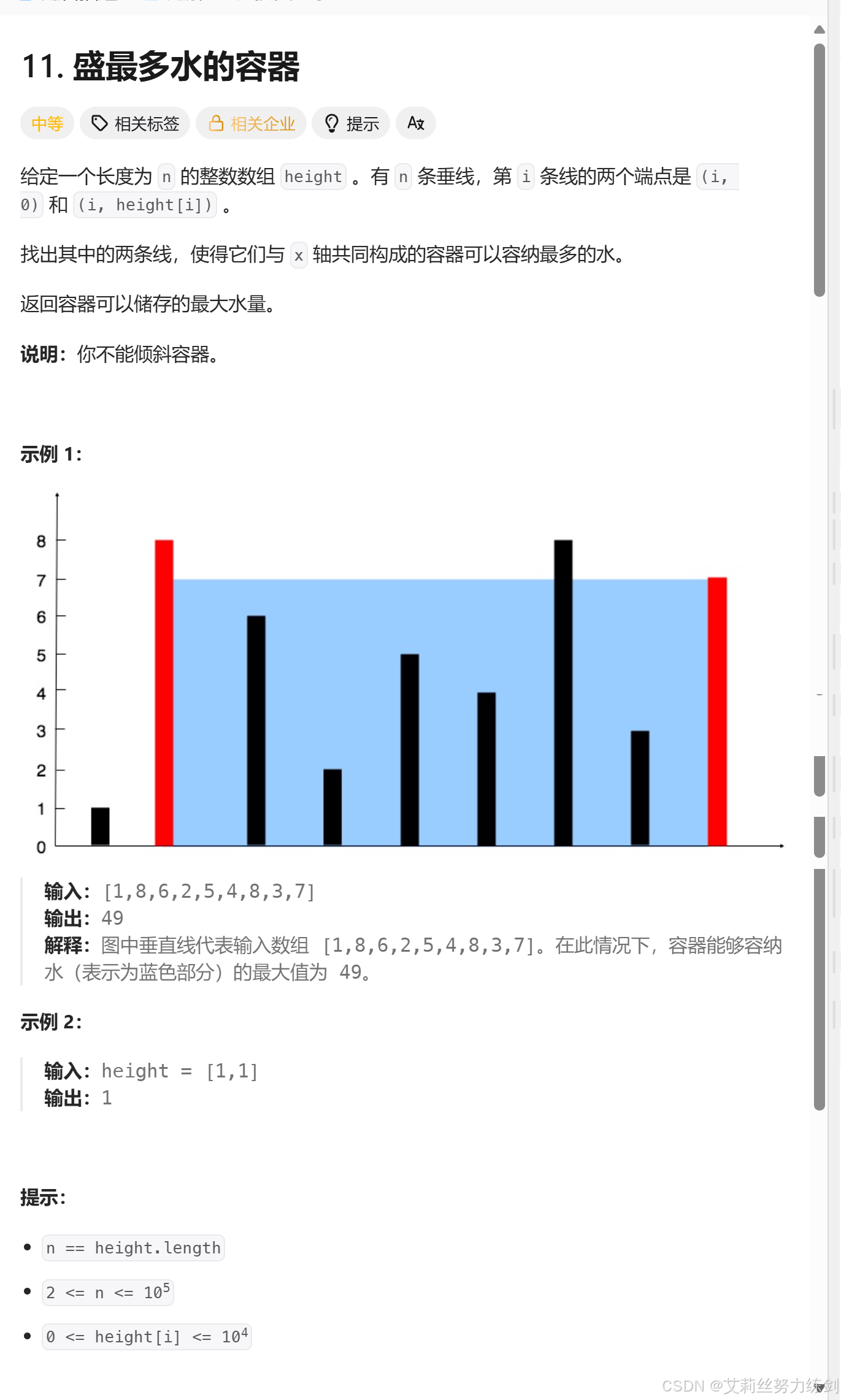
2.1 思路

2.1.1 暴力算法

这道题用暴力求解，最后会超时。

算法思路： 枚举出能构成的所有容器，找出其中容积最大的值。

容器容积的计算方式：

设两指针 i , j ，分别指向水槽板的最左端以及最右端，此时容器的宽度为 j - i 。由于 容器的高度由两板中的短板决定，因此可得容积公式： v = (j - i) * min( height[ i ], height[ j ] )。

代码演示：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int ret = 0;
        // 两层 for 枚举出所有可能出现的情况 
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                // 计算容积，找出最⼤的那⼀个 
                ret = max(ret, min(height[i], height[j]) * (j - i));
            }
        }
        return ret;
    }
};

2.1.2 双指针算法

双指针算法——

利用单调性，使用双指针来解决问题。 v = h * d（h即height，d即宽度），d = (right - left)。

2.2 算法流程

设两个指针 left ， right 分别指向容器的左右两个端点，此时容器的容积 :

v = (right - left) * min( height[ right ], height[ left ])。

容器的左边界为 height[ left ] ，右边界为 height[ right ] 。

（1）容器的宽度一定变小； （2）由于左边界较小，决定了水的高度。如果改变左边界，新的水面高度不确定，但是一定不会超过右边的柱子高度，因此容器的容积可能会增大； （3）如果改变右边界，无论右边界移动到哪里，新的水面高度一定不会超过左边界，也就是不会 超过现在的水面高度，但是由于容器的宽度减小，因此容器的容积一定会变小的。

由此可见，左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界，继续去判断下一个左右边界。

当我们不断重复上述过程，每次都可以舍去大量不必要的枚举过程，直到 left 与 right 相遇。期间产生的所有的容积里面的最大值，就是最终答案。

2.3 对撞指针——双指针算法的代码实现

代码演示：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0, right = height.size() - 1, ret = 0;
        while (left < right)
        {
            int v = min(height[left], height[right]) * (right - left);
            ret = max(ret, v);

            //移动指针
            if (height[left] >= height[right])
            {
                right--;
            }
            else
            {
                left++;
            }
        }
        return ret;
    }
};

时间复杂度：O(N)，空间复杂度：O(1)。

2.4 过程推算

本题整个的思路、算法原理、解题过程博主在纸上推导了一遍，大家可以参考一下！

结尾

往期回顾：

【优选算法必刷100题】第001~002题（双指针算法）：移动零、复写零问题求解

结语：本文内容到这里就结束了，大家不要忘记给博主“一键四连”哦！