直线上最多的点数
直线上最多的点数
给你一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
示例 1：
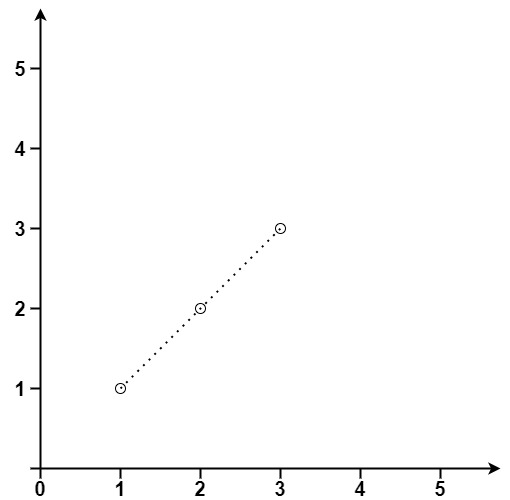
输入：points = [[1,1],[2,2],[3,3]]
输出：3示例 2：
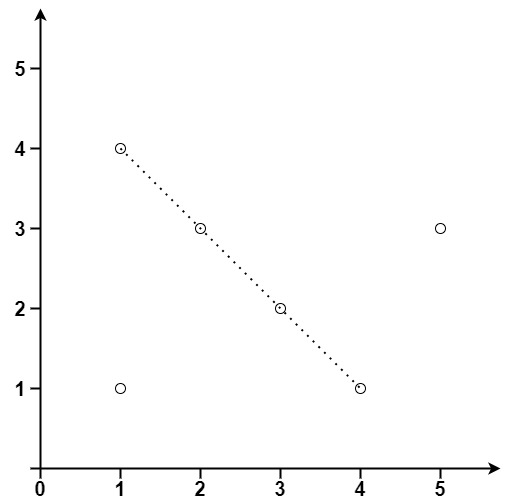
输入：points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出：4思路及解法
我们可以考虑枚举所有的点，假设直线经过该点时，该直线所能经过的最多的点数。
假设我们当前枚举到点 iii，如果直线同时经过另外两个不同的点 jjj 和 kkk，那么可以发现点 iii 和点 jjj 所连直线的斜率恰等于点 iii 和点 kkk 所连直线的斜率。
于是我们可以统计其他所有点与点 iii 所连直线的斜率，出现次数最多的斜率即为经过点数最多的直线的斜率，其经过的点数为该斜率出现的次数加一（点 iii 自身也要被统计）。
如何记录斜率
需要注意的是，浮点数类型可能因为精度不够而无法足够精确地表示每一个斜率，因此我们需要换一种方法来记录斜率。
一般情况下，斜率可以表示为
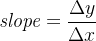
的形式，因此我们可以用分子和分母组成的二元组来代表斜率。但注意到存在形如
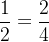
这样两个二元组不同，但实际上两分数的值相同的情况，所以我们需要将分数
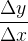
化简为最简分数的形式。
将分子和分母同时除以二者绝对值的最大公约数，可得二元组
。
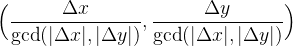
令
，
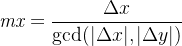
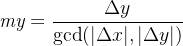
，则上述化简后的二元组为
。
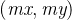
此外，因为分子分母可能存在负数，为了防止出现形如
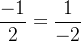
的情况，我们还需要规定分子为非负整数，如果
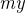
为负数，我们将二元组中两个数同时取相反数即可。
特别地，考虑到
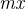
和
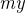
两数其中有一个为
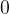
的情况（因为题目中不存在重复的点，因此不存在两数均为
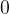
的情况），此时两数不存在数学意义上的最大公约数，因此我们直接特判这两种情况。当
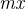
为 000 时，我们令
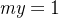
；当
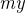
为
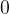
时，我们令
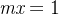
即可。
经过上述操作之后，即可得到最终的二元组
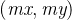
。在本题中，因为点的横纵坐标取值范围均为
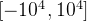
，所以斜率
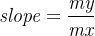
中，
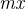
落在区间
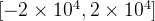
内，
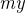
落在区间
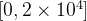
内。注意到
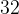
位整数的范围远超这两个区间，因此我们可以用单个
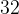
位整型变量来表示这两个整数。具体地，我们令
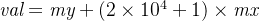
即可。
优化
最后我们再加四个小优化：
在点的总数量小于等于
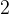
的情况下，我们总可以用一条直线将所有点串联，此时我们直接返回点的总数量即可； 当我们枚举到点
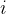
时，我们只需要考虑编号大于
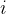
的点到点
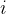
的斜率，因为如果直线同时经过编号小于点
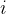
的点
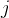
，那么当我们枚举到
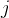
时就已经考虑过该直线了； 当我们找到一条直线经过了图中超过半数的点时，我们即可以确定该直线即为经过最多点的直线； 当我们枚举到点
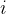
（假设编号从
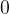
开始）时，我们至多只能找到
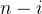
个点共线。假设此前找到的共线的点的数量的最大值为
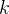
，如果有
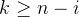
，那么此时我们即可停止枚举，因为不可能再找到更大的答案了。
class Solution {
public:
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a;
}
int maxPoints(vector<vector<int>>& points) {
int n = points.size();
if (n <= 2) {
return n;
}
int ret = 0;
for (int i = 0; i < n; i++) {
if (ret >= n - i || ret > n / 2) {
break;
}
unordered_map<int, int> mp;
for (int j = i + 1; j < n; j++) {
int x = points[i][0] - points[j][0];
int y = points[i][1] - points[j][1];
if (x == 0) {
y = 1;
} else if (y == 0) {
x = 1;
} else {
if (y < 0) {
x = -x;
y = -y;
}
int gcdXY = gcd(abs(x), abs(y));
x /= gcdXY, y /= gcdXY;
}
mp[y + x * 20001]++;
}
int maxn = 0;
for (auto& [_, num] : mp) {
maxn = max(maxn, num + 1);
}
ret = max(ret, maxn);
}
return ret;
}
};复杂度分析
时间复杂度：
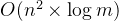
，其中
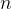
为点的数量，
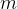
为横纵坐标差的最大值。最坏情况下我们需要枚举所有
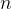
个点，枚举单个点过程中需要进行
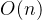
次最大公约数计算，单次最大公约数计算的时间复杂度是
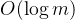
，因此总时间复杂度为
。
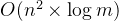
空间复杂度：
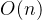
，其中
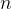
为点的数量。主要为哈希表的开销。
腾讯云开发者
