几何非线性| 应变张量

fem178

发布于 2024-04-30 17:39:15

1060

发布于 2024-04-30 17:39:15

文章被收录于专栏：数值分析与有限元编程数值分析与有限元编程

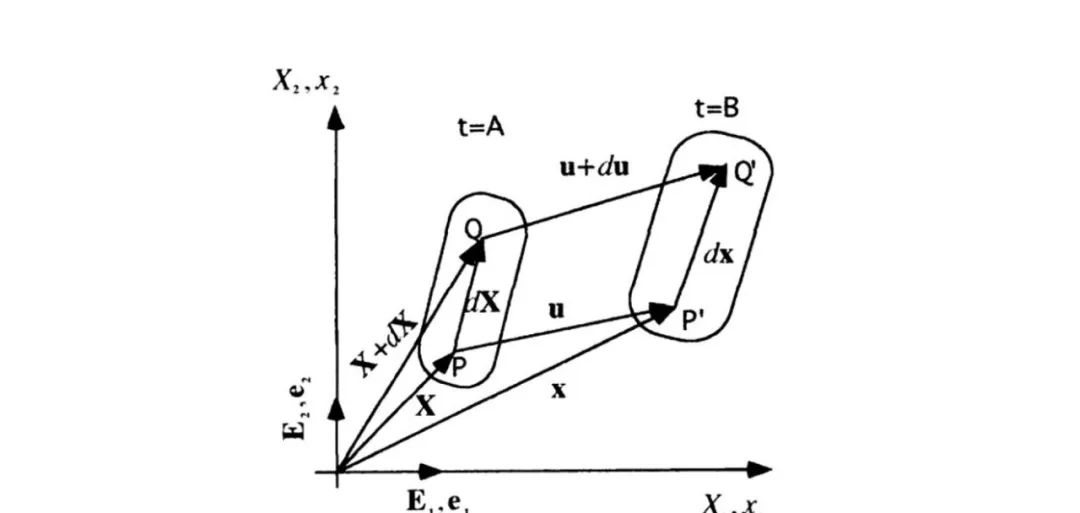
考虑二维空间中的一个连续体,分别是其中的两个物质点，如图3.1所示。在连续体变形前(时刻)引入物质坐标系，另外，在连续体变形之后(时刻)引入空间坐标系。两个坐标系相关的基向量分别为和。

按照描述，位置矢量

\begin{split} \mathbf X &= X_1 \mathbf E_1 + X_2 \mathbf E_2 \\ \end{split} \tag{1.1}

\begin{split} \mathbf x &= x_1 \mathbf E_1 + x_2 \mathbf E_2 \\ \end{split} \tag{1.2}

位移矢量

\mathbf u = u_1 \mathbf E_1 + u_2 \mathbf E_2 \tag{2}

变形前后的位置矢量之间的关系为

\begin{split} \mathbf x &= \mathbf X + \mathbf u \\ d\mathbf x &= d \mathbf X + d \mathbf u \end{split} \tag{3}

使用坐标系,变形后的物体中任意点的位置矢量：

\begin{split} x_1 &= x_1(X_1,X_2) \\ \end{split} \tag{4.1}

\begin{split} x_2 &= x_2(X_1,X_2) \\ \end{split} \tag{4.2}

变形前的在变形后移动到新的位置,记

\begin{split} dS^2 &= d \mathbf X \cdot d \mathbf X = dX_1dX_1+dX_2dX_2\\ ds^2 &= d \mathbf x \cdot d \mathbf x = dx_1dx_1+dx_2dx_2 \end{split} \quad (5)

于是

\Delta^2= ds^2-dS^2 = d \mathbf x \cdot d \mathbf x-d \mathbf X \cdot d \mathbf X \quad (6)

定义梯度算子

\begin{split} \nabla(\cdot) &= \frac{\partial(\cdot) } {\partial\mathbf X}\\ \nabla_x(\cdot) &= \frac{\partial(\cdot) } {\partial\mathbf x} \end{split} \quad (7)

则

\begin{split} d\mathbf x &= \nabla(\mathbf x) d \mathbf X = \mathbf F \cdot d \mathbf X = \frac{\partial\mathbf x(\mathbf X,t) }{\partial\mathbf X}d \mathbf X \\ d\mathbf u &= \nabla(\mathbf u) d \mathbf X = \mathbf H\cdot d \mathbf X \end{split} \quad (8)

其中，叫做变形梯度，叫做位移梯度。

由(3)可得

\begin{split} \mathbf H &= \nabla(\mathbf x -\mathbf X) \\ &= \nabla \mathbf x -\nabla \mathbf X \\ &= \frac{\partial\mathbf x}{\partial\mathbf X}- \frac{\partial\mathbf X}{\partial\mathbf X} \\ &= \mathbf F - \mathbf I \end{split} \tag{9}

\begin{split} \Delta^2 &= ds^2-dS^2\\ &=(\mathbf F \cdot d \mathbf X)(\mathbf F \cdot d \mathbf X) - d \mathbf X \cdot d \mathbf X \\ &= (d \mathbf X\cdot \mathbf F^T)(\mathbf F \cdot d \mathbf X)-d \mathbf X \cdot d \mathbf X\\ &=d\mathbf X(\mathbf F^T\mathbf F)d\mathbf X - d\mathbf X(\mathbf I)d\mathbf X\\ &=d\mathbf X(\mathbf F^T\mathbf F-\mathbf I)d\mathbf X \end{split} \tag{10}

定义应变

\mathbf E = \frac{1}{2}(\mathbf F^T\mathbf F-\mathbf I) \tag{11}

则

\Delta^2 = 2 d\mathbf X (\mathbf F^T\mathbf F-\mathbf I) d\mathbf X \tag{12}

由(9)可得

\mathbf F = \mathbf H + \mathbf I \tag{13}

则

\mathbf E = \frac{1}{2}((\mathbf H + \mathbf I)^T(\mathbf H + \mathbf I)-\mathbf I) \tag{14}

展开，得

\mathbf E = \frac{1}{2}(\mathbf H + \mathbf H^T + \mathbf H^T \mathbf H ) \tag{15}

忽略高阶量，线性化的拉格朗日应变张量为

\hat{\mathbf E }= \frac{1}{2}(\mathbf H + \mathbf H^T ) \tag{16}

[例1] 给出如下的运动

\begin{split} x_1 &= X_1 - X_2X_3\\ x_2 &= X_2 + X_1X_3\\ x_3 &= X_3 + \phi(X_1,X_2)\\ \end{split}

则由得

\begin{split} u_1 &= - X_2X_3\\ u_2 &= X_1X_3\\ u_3 &= \phi(X_1,X_2)\\ \end{split}

作求导运算

\begin{split} \frac{\partial u_1 }{\partial X_1} &= 0 \\ \frac{\partial u_1 }{\partial X_2} &= -X_3\\ \frac{\partial u_1 }{\partial X_3} &= -X_2\\ \frac{\partial u_2 }{\partial X_1} &= X_3 \\ \frac{\partial u_2 }{\partial X_2} &= 0\\ \frac{\partial u_2 }{\partial X_3} &= X_1\\ \frac{\partial u_3 }{\partial X_1} &= \frac{\partial \phi }{\partial X_1} \\ \frac{\partial u_3 }{\partial X_2} &= \frac{\partial \phi }{\partial X_2} \\ \frac{\partial u_3 }{\partial X_3} &= 0\\ \end{split}

位移梯度

\begin{split} \mathbf H &= \frac{\partial \mathbf u_i }{\partial \mathbf X_j } \\ &= \begin{bmatrix} \frac{\partial u_1 }{\partial X_1} & \frac{\partial u_1 }{\partial X_2} & \frac{\partial u_1 }{\partial X_3} \\ \frac{\partial u_2 }{\partial X_1} & \frac{\partial u_2 }{\partial X_2} & \frac{\partial u_2 }{\partial X_3} \\ \frac{\partial u_3 }{\partial X_1} & \frac{\partial u_3 }{\partial X_2} & \frac{\partial u_3 }{\partial X_3} \\ \end{bmatrix} \\ &= \begin{bmatrix} 0 & -X_3 & -X_2 \\ X_3 & 0 & X_1\\ \frac{\partial \phi }{\partial X_1} & \frac{\partial \phi }{\partial X_2} & 0\\ \end{bmatrix} \\ \end{split}

本文参与腾讯云自媒体分享计划，分享自微信公众号。

原始发表：2024-04-28，如有侵权请联系 cloudcommunity@tencent.com 删除

partial

split

本文分享自数值分析与有限元编程微信公众号，前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体分享计划，欢迎热爱写作的你一起参与！

partial

split

登录后参与评论

0 条评论

热度

几何非线性| 应变张量

几何非线性| 应变张量

社区

活动

资源

关于

腾讯云开发者

热门产品

热门推荐

更多推荐