机器学习中牛顿法凸优化的通俗解释
版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/red_stone1/article/details/80821760
红色石头的个人网站:redstonewill.com
之前,我发过一篇文章,通俗地解释了梯度下降算法的数学原理和推导过程,推荐一看。链接如下:
我们知道,梯度下降算法是利用梯度进行一阶优化,而今天我介绍的牛顿优化算法采用的是二阶优化。本文将重点讲解牛顿法的基本概念和推导过程,并将梯度下降与牛顿法做个比较。
1. 牛顿法求解方程的根
有时候,在方程比较复杂的情况下,使用一般方法求解它的根并不容易。牛顿法通过迭代的方式和不断逼近的思想,可以近似求得方程较为准确的根。
牛顿法求根的核心思想是泰勒一阶展开。例如对于方程 f(x) = 0,我们在任意一点 x0 处,进行一阶泰勒展开:
f(x)=f(x0)+(x−x0)f′(x0)f(x)=f(x0)+(x−x0)f′(x0)
f(x)=f(x_0)+(x-x_0)f'(x_0)
令 f(x) = 0,带入上式,即可得到:
x=x0−f(x0)f′(x0)x=x0−f(x0)f′(x0)
x=x_0-\frac{f(x_0)}{f'(x_0)}
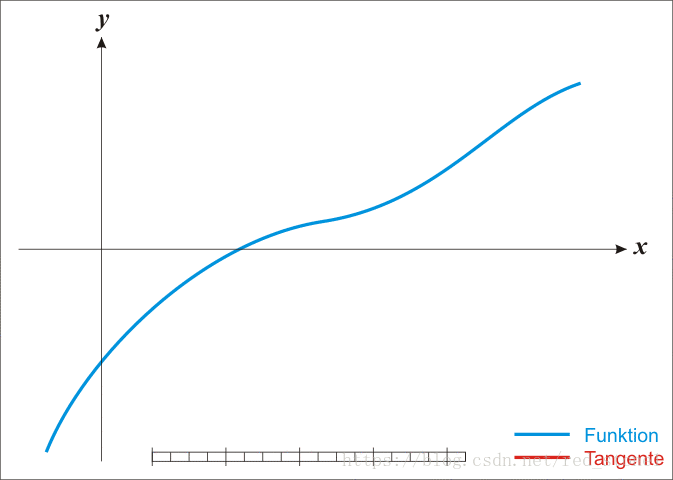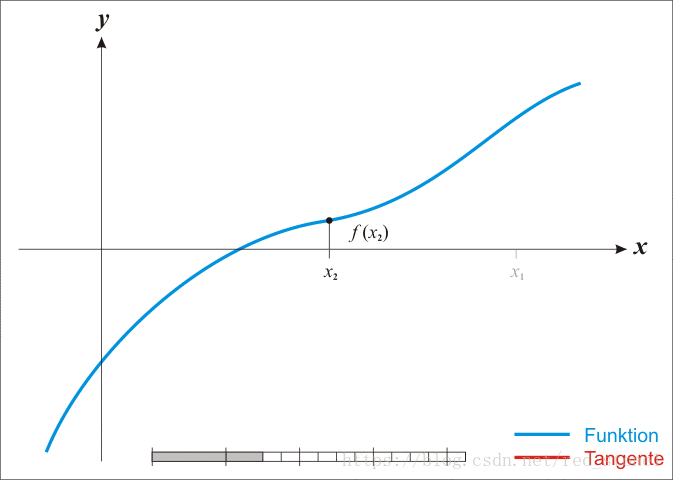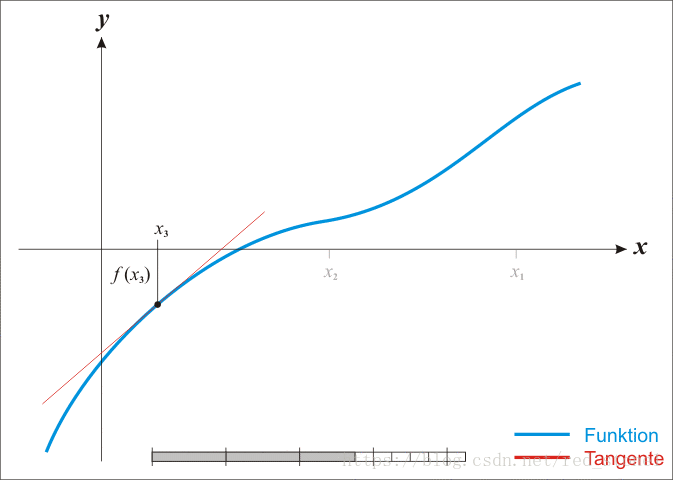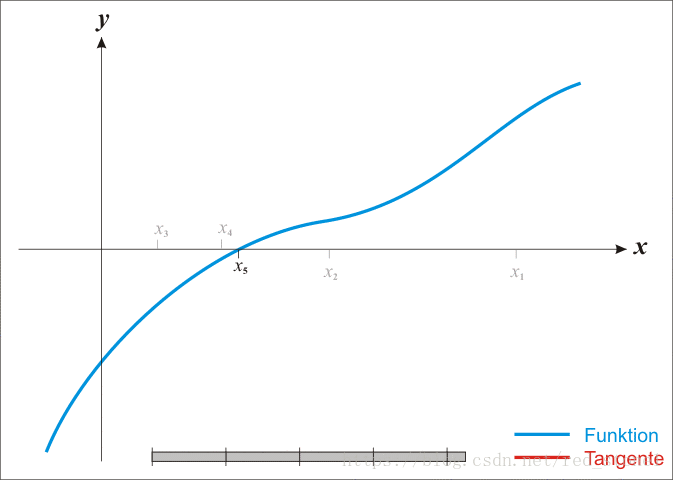
注意,这里使用了近似,得到的 x 并不是方程的根,只是近似解。但是,x 比 x0 更接近于方程的根。效果如下图所示:
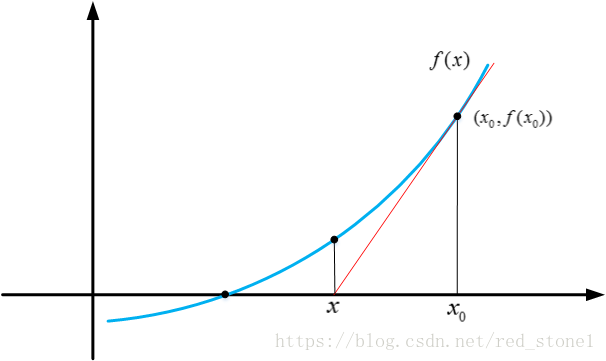
xn+1=xn−f(xn)f′(xn)xn+1=xn−f(xn)f′(xn)
x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}
经过一定次数的有效迭代后,一般都能保证在方程的根处收敛。下面给出整个迭代收敛过程的动态演示。
2. 牛顿法凸优化
上一部分介绍牛顿法如何求解方程的根,这一特性可以应用在凸函数的优化问题上。
机器学习、深度学习中,损失函数的优化问题一般是基于一阶导数梯度下降的。现在,从另一个角度来看,想要让损失函数最小化,这其实是一个最值问题,对应函数的一阶导数 f’(x) = 0。也就是说,如果我们找到了能让 f’(x) = 0 的点 x,损失函数取得最小值,也就实现了模型优化目标。
现在的目标是计算 f’(x) = 0 对应的 x,即 f’(x) = 0 的根。转化为求根问题,就可以利用上一节的牛顿法了。
与上一节有所不同,首先,对 f(x) 在 x0 处进行二阶泰勒展开:
f(x)=f(x0)+(x−x0)f′(x0)+12(x−x0)2f′′(x0)f(x)=f(x0)+(x−x0)f′(x0)+12(x−x0)2f″(x0)
f(x)=f(x_0)+(x-x_0)f'(x_0)+\frac12(x-x_0)^2f''(x_0)
上式成立的条件是 f(x) 近似等于 f(x0)。令 f(x) = f(x0),并对 (x - x0) 求导,可得:
x=x0−f′(x0)f′′(x0)x=x0−f′(x0)f″(x0)
x=x_0-\frac{f'(x_0)}{f''(x_0)}
同样,虽然 x 并不是最优解点,但是 x 比 x0 更接近 f’(x) = 0 的根。这样,就能得到最优化的迭代公式:
xn+1=xn−f′(xn)f′′(xn)xn+1=xn−f′(xn)f″(xn)
x_{n+1}=x_n-\frac{f'(x_n)}{f''(x_n)}
通过迭代公式,就能不断地找到 f’(x) = 0 的近似根,从而也就实现了损失函数最小化的优化目标。
3. 梯度下降 VS 牛顿法
现在,分别写出梯度下降和牛顿法的更新公式:
xn+1=xn−ηf′(xn)xn+1=xn−ηf′(xn)
x_{n+1}=x_n-\eta f'(x_n)
xn+1=xn−f′(xn)f′′(xn)xn+1=xn−f′(xn)f″(xn)
x_{n+1}=x_n-\frac{f'(x_n)}{f''(x_n)}
梯度下降算法是将函数在 xn 位置进行一次函数近似,也就是一条直线。计算梯度,从而决定下一步优化的方向是梯度的反方向。而牛顿法是将函数在 xn 位置进行二阶函数近似,也就是二次曲线。计算梯度和二阶导数,从而决定下一步的优化方向。一阶优化和二阶优化的示意图如下所示:
梯度下降,一阶优化:

牛顿法,二阶优化:

以上所说的是梯度下降和牛顿法的优化方式差异。那么谁的优化效果更好呢?
首先,我们来看一下牛顿法的优点。第一,牛顿法的迭代更新公式中没有参数学习因子,也就不需要通过交叉验证选择合适的学习因子了。第二,牛顿法被认为可以利用到曲线本身的信息, 比梯度下降法更容易收敛(迭代更少次数)。如下图是一个最小化一个目标方程的例子, 红色曲线是利用牛顿法迭代求解, 绿色曲线是利用梯度下降法求解。显然,牛顿法最优化速度更快一些。

然后,我们再来看一下牛顿法的缺点。我们注意到牛顿法迭代公式中除了需要求解一阶导数之外,还要计算二阶导数。从矩阵的角度来说,一阶导数和二阶导数分别对应雅可比矩阵(Jacobian matrix)和海森矩阵(Hessian matrix)。
Jacobian 矩阵:

Hessian 矩阵:

牛顿法不仅需要计算 Hessian 矩阵,而且需要计算 Hessian 矩阵的逆。当数据量比较少的时候,运算速度不会受到大的影响。但是,当数据量很大,特别在深度神经网络中,计算 Hessian 矩阵和它的逆矩阵是非常耗时的。从整体效果来看,牛顿法优化速度没有梯度下降算法那么快。所以,目前神经网络损失函数的优化策略大多都是基于梯度下降。
值得一提的是,针对牛顿法的缺点,目前已经有一些改进算法。这类改进算法统称拟牛顿算法。比较有代表性的是 BFGS 和 L-BFGS。
BFGS 算法使用近似的方法来计算 Hessian 矩阵的逆,有效地提高了运算速度。但是仍然需要将整个 Hessian 近似逆矩阵存储起来,空间成本较大。
L-BFGS 算法是对BFGS 算法的改进,不需要存储 Hessian 近似逆矩阵, 而是直接通过迭代算法获取本轮的搜索方向,空间成本大大降低。
总的来说,基于梯度下降的优化算法,在实际应用中更加广泛一些,例如 RMSprop、Adam等。但是,牛顿法的改进算法,例如 BFGS、L-BFGS 也有其各自的特点,也有很强的实用性。