图解LeetCode——662. 二叉树最大宽度（难度：中等）

一、题目

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

二、示例

2.1> 示例 1：

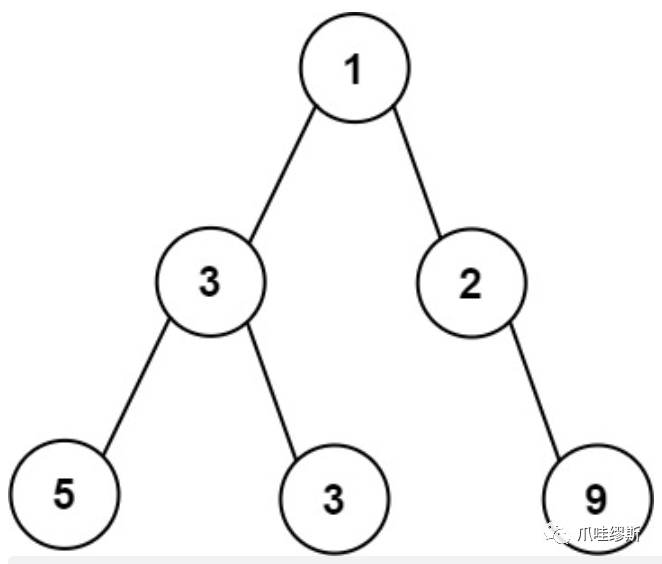
【输入】root = [1,3,2,5,3,null,9] 【输出】4 【解释】最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

2.2> 示例 2：

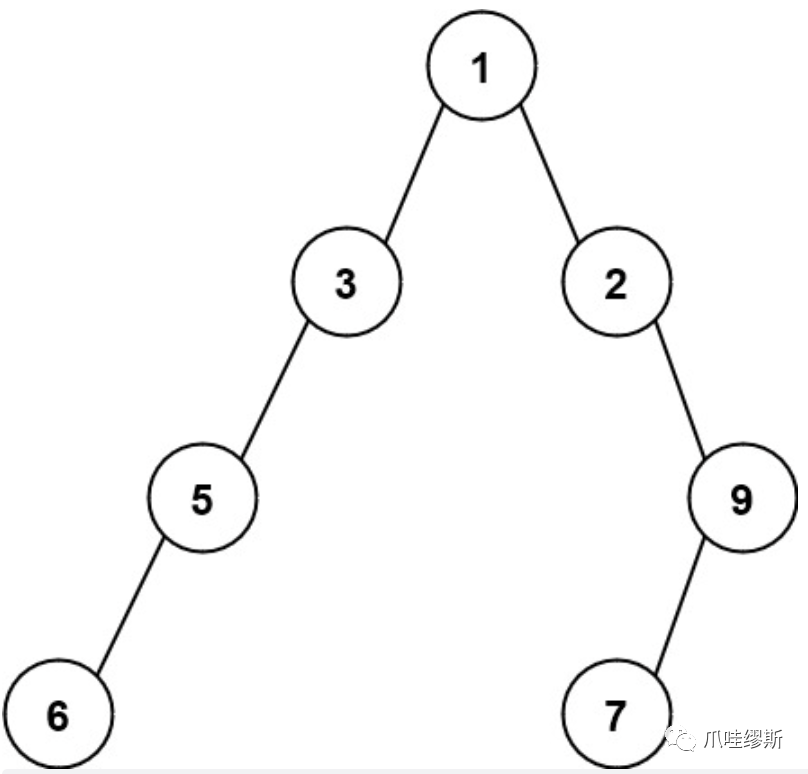
【输入】root = [1,3,2,5,null,null,9,6,null,7] 【输出】7 【解释】最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

2.3> 示例 3：

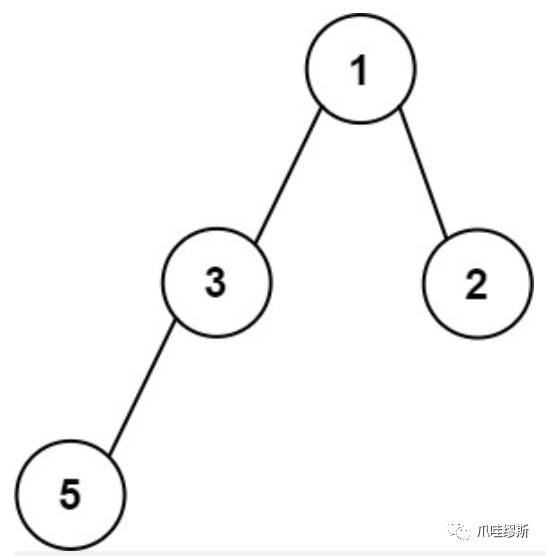
【输入】root = [1,3,2,5] 【输出】2 【解释】最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

• • 树中节点的数目范围是 [1, 3000]
• • -100 <= Node.val <= 100

三、解题思路

3.1> 思路1：广度优先 + 节点编号

根据题意，要统计树的最大宽度是所有层中最大的宽度。那么，既然涉及到要对每一层的树节点进行操作，我们会很自然的想到要用广度优先遍历。但是，如果采用广度优先算法，我们遇到的一个麻烦就是，如何去处理空节点？类似于，一个节点它只有一个子节点。这种空节点也是需要被统计在内的。所以，首先考虑的一个办法是，采用构建一个空的虚拟节点，由于题目中提示：-100 <= Node.val <= 100，所以我们可以指定虚拟节点的val值为-101，即：如果发现没有左子节点或者右子节点的话，我们就创建一个new TreeNode(-101, null, null)。这样，就可以构建一个全都有字节点的二叉树了。

那么，由于没有子节点就创建空的虚拟节点，如果不添加某个判断条件，这种构建空节点的操作将会无限的创建下去。那么我们可以通过判断某一层的节点值是否有非-101的，如果节点的val值都是-101，则说明这一层都是空节点，结束循环操作。如下图所示：

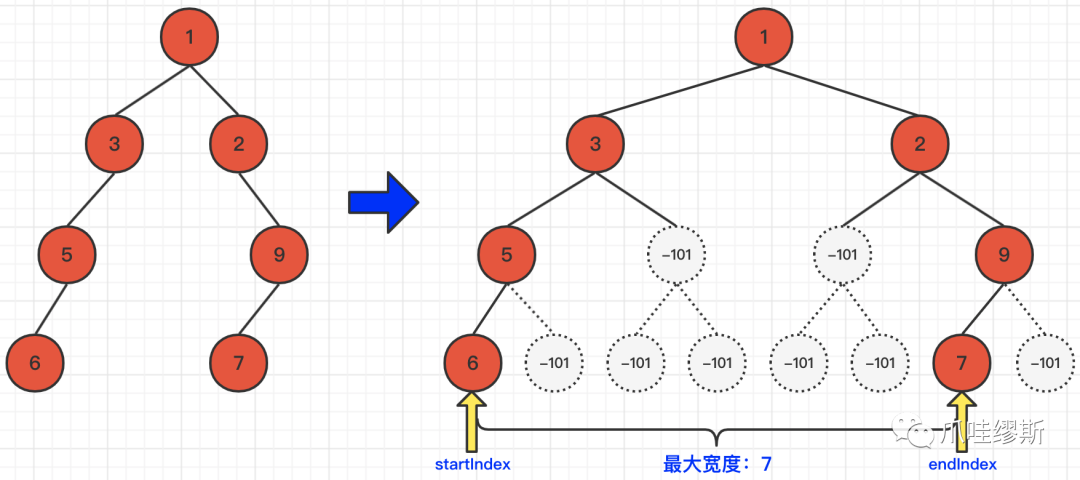
构建虚拟的空节点虽然可以满足题目的计算逻辑，但是，由于要大量的创建空的虚拟节点，而且越到层级越深且该层级真是节点越少，那么创建的空节点将会非常的多，那么在提交的时候，就会造成超出内存限制的问题。

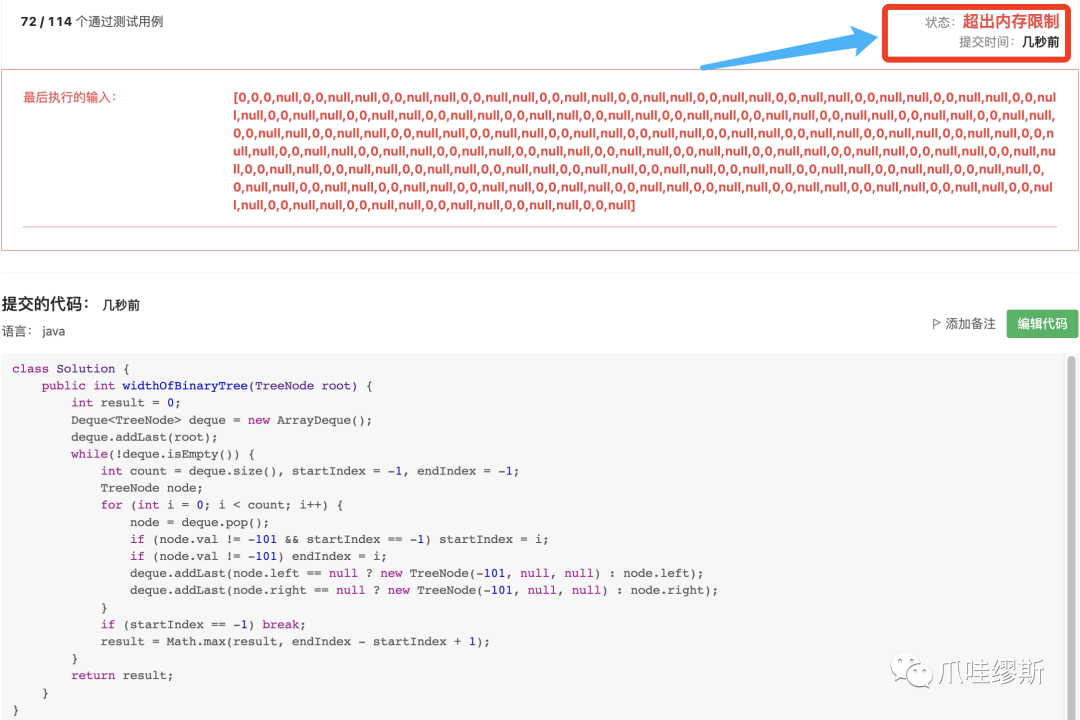
那么，除了创建虚拟节点，我们还有什么办法呢？其实，通过观察我们会发现一个规律：假设根节点的编号为1，左子节点为2，右子节点为3……以此类推，会得出如下结论：

root的编号=N root.left的编号=2N root.right的编号=2N + 1

那么我们通过编号就可以计算同层中两个节点之间的距离了。我们还是以root = [1,3,2,5,null,null,9,6,null,7]为例，看看通过编号怎么去解题。

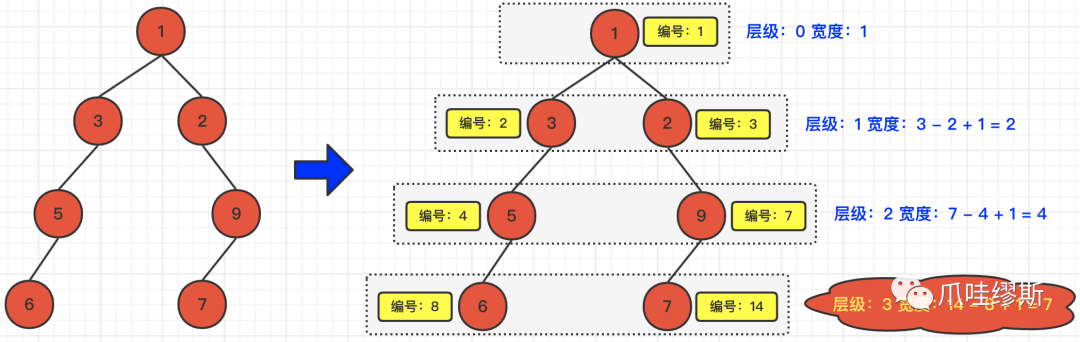
对于编号的存储，我们可以创建一个对象，里面包含编号和TreeNode这两个变量，也可以使用JDK内置的Pair对象，由于本题中，节点的val值没有任何用处，所以，编号我就存储到了val属性值中，这样更易于存储和获取。具体实现，请参照：4.1> 代码1：广度优先 + 节点编号

3.2> 思路2：深度优先 + 节点编号

既然广度优先可以解决该问题，那么理论上，通过深度优先也是可以解题的。由于深度优先，是先从最上层沿着一条父子关系链遍历的下层，类似一个分支一个分支的去遍历，那么，我们就需要一个Map来帮助我们存储层级与当前层级最小值的对应关系了——即：key=level，value=minValue。那么，我们每当遍历一个节点时，就可以通过当前的level值去获取最小节点值：

如果Map中不存在该level的最小值，则将该节点的值放入到map中作为当前level下的最小值； 如果存在，那么则用当前节点值node.val减去从Map中获取的当前level下的最小值；

我们还是以root = [1,3,2,5,null,null,9,6,null,7]为例，看看通过深度优先怎么去解题。请见下图：

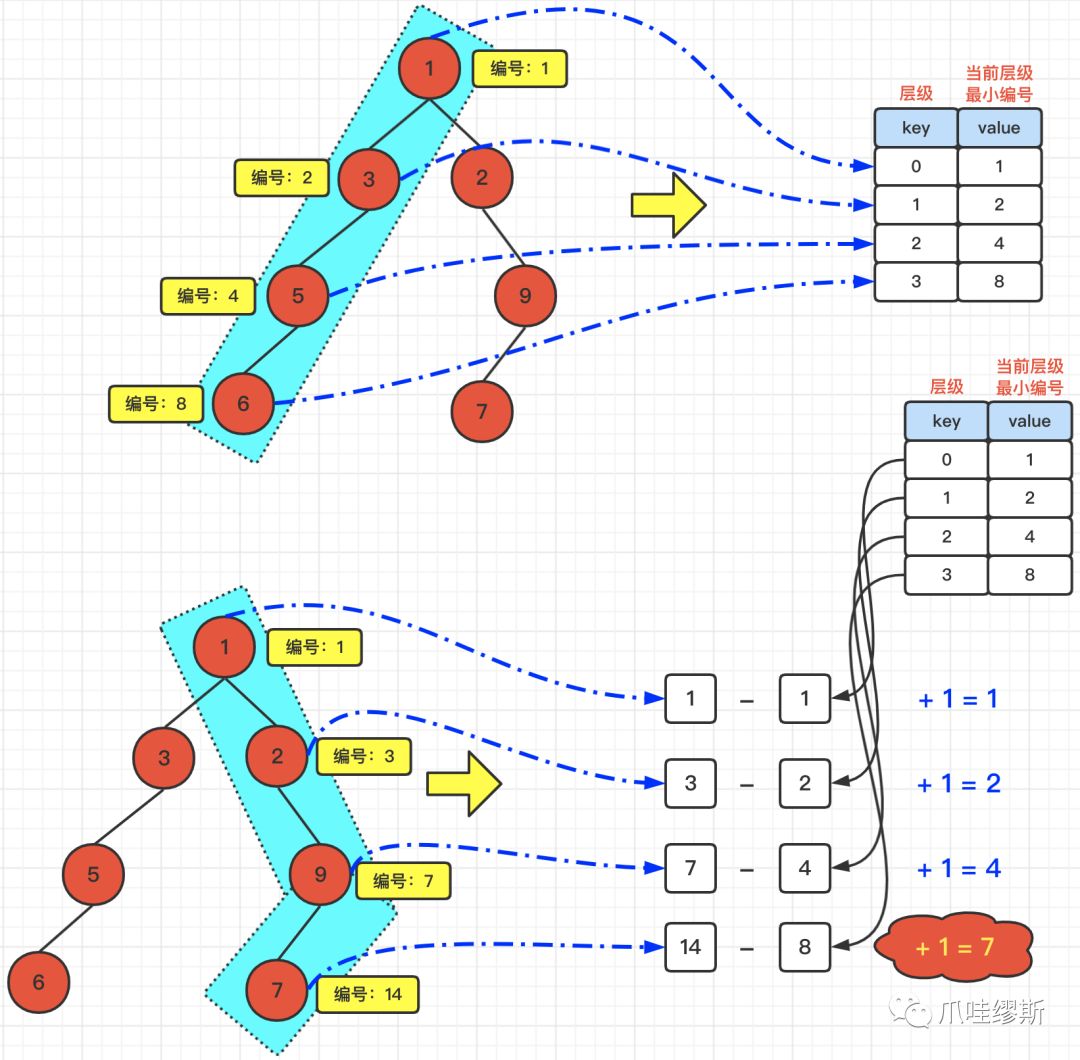
针对于采用深度优先算法的具体实现，请参照：4.2> 代码2：深度优先 + 节点编号

四、代码实现

4.1> 代码1：广度优先 + 节点编号

class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        int result = 0;
        Deque<TreeNode> deque = new ArrayDeque();
        deque.addLast(new TreeNode(1, root.left, root.right));
        while(!deque.isEmpty()) {
            int count = deque.size(), startIndex = -1, endIndex = -1;
            for (int i = 0; i < count; i++) {
                TreeNode node = deque.pop();
                endIndex = node.val;
                if (startIndex == -1) startIndex = node.val;
                if (node.left != null) deque.addLast(new TreeNode(node.val * 2, node.left.left, node.left.right));
                if (node.right != null) deque.addLast(new TreeNode(node.val * 2 + 1, node.right.left, node.right.right));
            }
            result = Math.max(result, endIndex - startIndex + 1);
        }
        return result;
    }
}

4.2> 代码2：深度优先 + 节点编号

class Solution {
    int result = 0;
    Map<Integer, Integer> minValue = new HashMap();
    public int widthOfBinaryTree(TreeNode root) {
        depth(root, 1, 0);
        return result;
    }

    public void depth(TreeNode node , int nodeIndex, int level) {
        if (node == null) return;
        minValue.putIfAbsent(level, nodeIndex);
        result = Math.max(result, nodeIndex - minValue.get(level) + 1);
        depth(node.left, 2 * nodeIndex, level + 1);
        depth(node.right, 2 * nodeIndex + 1, level + 1);
    }
}