【KMP】KMP算法的一些小理解&总结

半生瓜的blog

发布于 2023-05-13 14:25:11

4190

文章被收录于专栏：半生瓜のblog半生瓜のblog

KMP

相关补充及内容来源和给我的一些启发
- 《代码随想录》
- labuladong-有限状态机之 KMP 字符匹配算法

我想对你说:
- 其实我感觉，写完本文我其实还不是特别透彻，也许在三刷或者更多刷的时候，或者说也许在未来的某一刻我会突然顿悟，到时候我可能还会更新一篇文章。
- 希望这篇文章能够给你一些启发。

前言:
- 以下内容中，我们称要匹配的字符串为模式串，使用模式串去匹配看是否存在该子串的叫文本串。
  - 即，使用模式串在文本串中匹配，看文本串中是否存在该模式串。
我们以力扣——28. 找出字符串中第一个匹配项的下标为例。
先弄清楚暴力怎么解决。

class Solution {
public:
    int strStr(string haystack, string needle) {
        int hs = haystack.size();
        int ns = needle.size();
        for(int i = 0; i < hs;i++){
            int tmp = i;// 保存开始匹配i的位置
            for(int j = 0;j < ns;j++){
                if(haystack[i] != needle[j]){
                    i = tmp;// 将i重置回去
                    break;
                }else{
                    if(j == ns-1)return tmp;// 相等并且已经到达结尾模式串结尾
                    i++;// 继续走
                }
            }
        }
        return -1;
    }
};

从上述代码可以看出，我们每次匹配失败就会从文本串下一个位置重新匹配模式串。
KMP算法就是要利用之前已经匹配过的信息，为后面匹配所用。O(n²)——>O(n)
那么我们如何例如之前匹配过的信息呢?
- 使用next数组!
求next数组的这个过程就是在求以首字母开头的各个子串的最长相等前后缀
- 什么是最长相等前后缀？
  - 前缀: 不包括最后一个字符的所有以第一个字符为开头的连续子串
  - 后缀: 不包括第一个字符的所有以最后一个字符为结尾的连续子串
  - 最长相等前后缀: 即如字面意思，前缀后缀中，最长的相等连续子串。
  - 举例: abfab，最长相等前后缀为前缀ab，后缀ab,为2。
不同的人,next数组的写法会有所不同，本代码中，我们不进行整体右移或是什么操作，求出来next数组是什么，我们的前缀表就用什么。
- 核心思想是相同的，只是在具体的使用上回有所差异。
如何求next数组?
- 具体步骤:
  - 初始化
  - 前后缀相同情况
  - 前后缀不同情况
- 补充:
  - 这里有些动态规划那味儿，根据当前的状态，并且结合之前的匹配状态，推出当前next数组的值。
- 实际操作:
  - i指向前缀末尾,j指向后缀末尾，从视觉上来看，就是i在后面，j在前面。i负责向后遍历，j则复杂一些，需要根据匹配情况进行向前/后调整。其实j既是下标，也是计数。i则为控制当前所求的子串是哪个。
  - 可以理解为，我们有个固定的i去指向子串尾部，但是j会随着匹配情况进行前移动或后移；
  - 其中，回退while语句的控制条件中的j>0，是因为最多只能退到字符串开头。即如果一直不相等，最终使得j=next[0];

下面我们好好说下j的作用，例如求:aabaa的最长相等前后缀，即next[4]。

要求next[4]，我们首先需要求出next[3],即aaba的最长相等前后缀。如下图所示(为j移动后的结果)，因为s[j]==s[i]，所以j++，j=1next[3]=1。

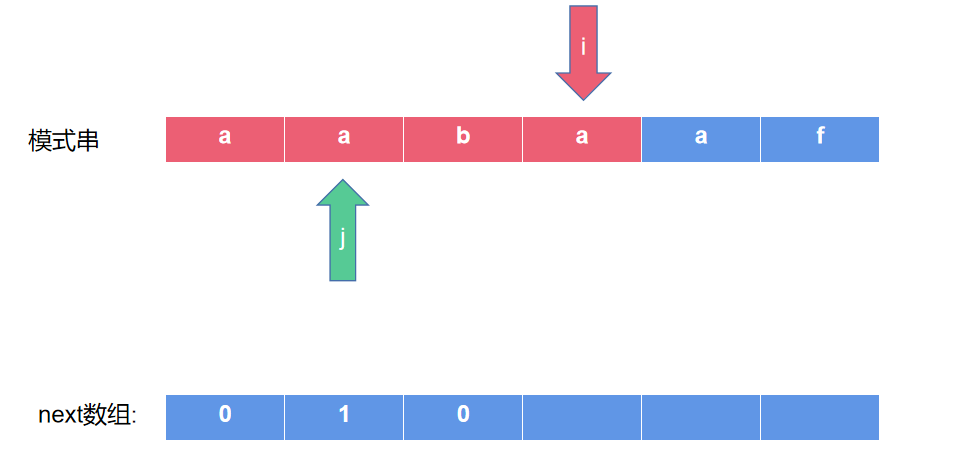
之后i++,我们开始求aabaa的最长相等前后缀。如下图所示。

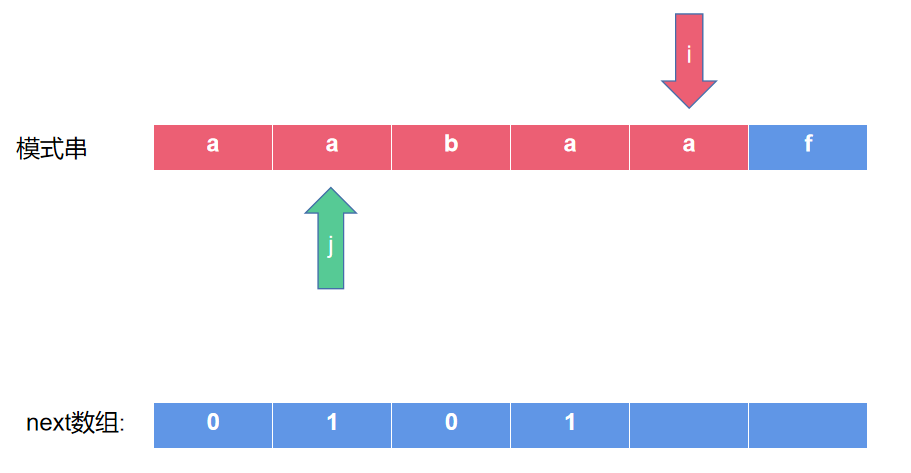
s[i] == s[j],j++,next[4]=2;
这是借助上一步的j=1得来的，可以理解为，当前i的前一个位置，有一个a,在j的前一个位置，即j-1处，也有一个a,因为这样，所以上一步才j++,使得j=1。即next[3]=1。
现在，s[j] = a,s[i] = a,s[j]==s[i]，相等，j在之前的基础上再次++,可以在之前基础上的条件是什么，就是现在的前后缀相等(j-1 i-1这两个对应的字符也相等)，即s[j]==s[i]，相等则推出s[j-1]+s[j]==s[i-1]+s[i],此时j=2。即next[4]=2。
否则假如当前s[j]!=s[i]，即不能再能延长公共前后缀了，那么j就回退，直到相等，或是j=0，如求aabaaf的最长相等前后缀。如下图所示:

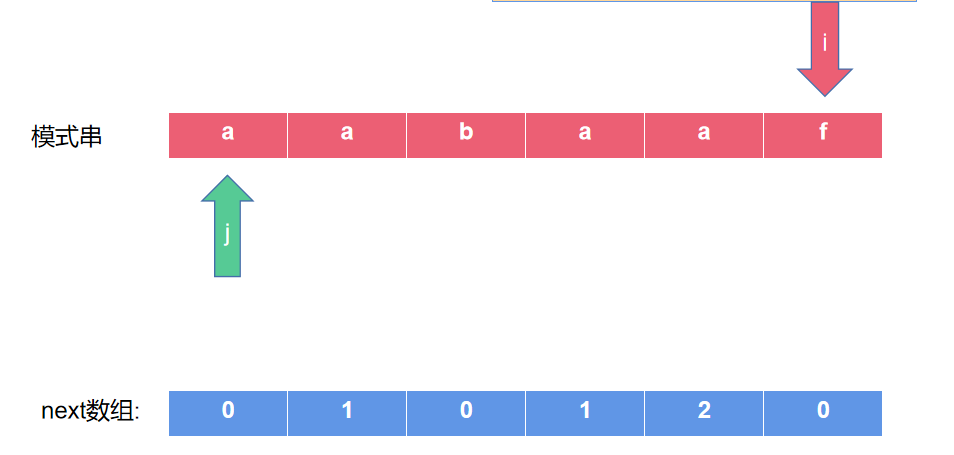
回退到了开头，next[5]=0,但是如果我们将f换成a,如下图所示:

不相等，开始回退，

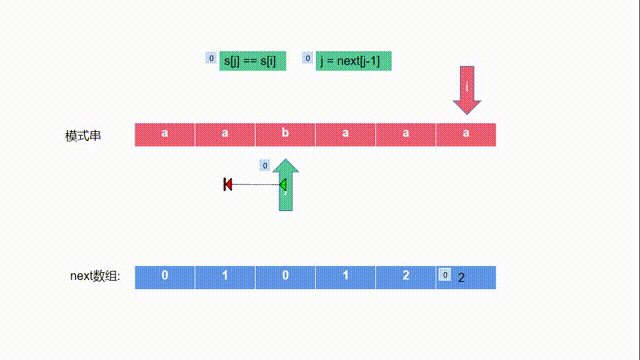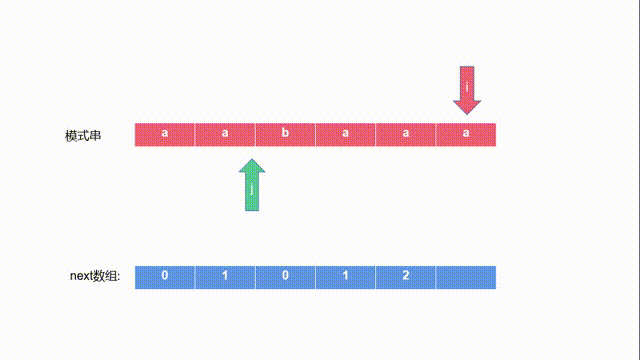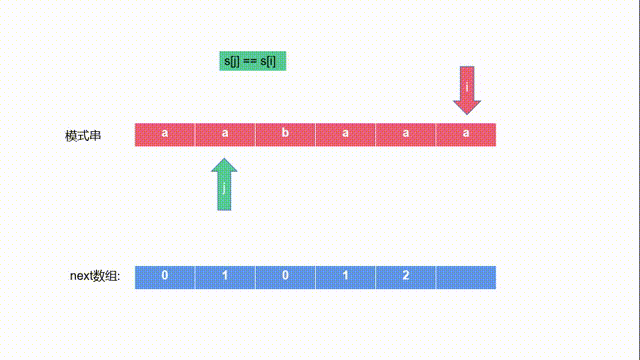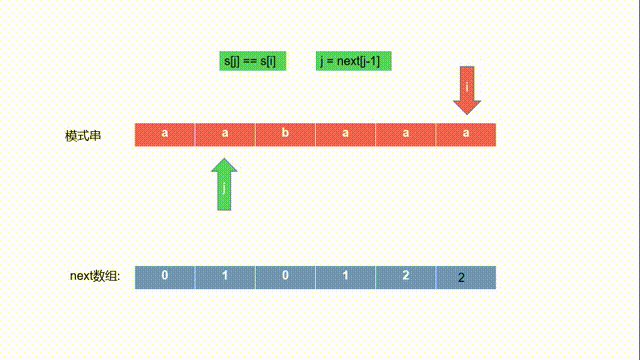
补充理解，为什么j=next[j-1]了，s[j]==s[i]就停止了，不用在往前判断，因为就是从前面判断过来的，因为前面j-1和i-1也相等，所以才行。
下面给出求next数组的动画:

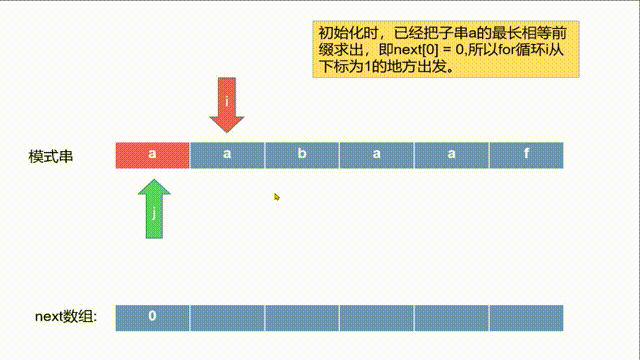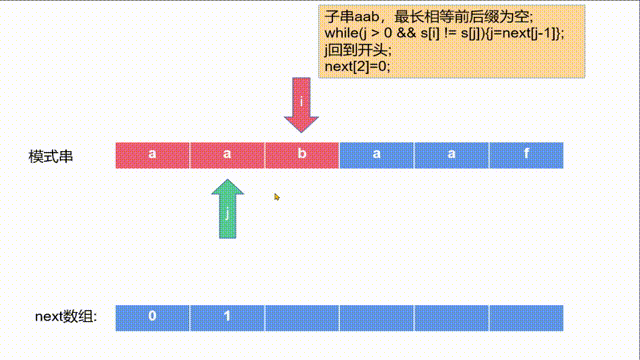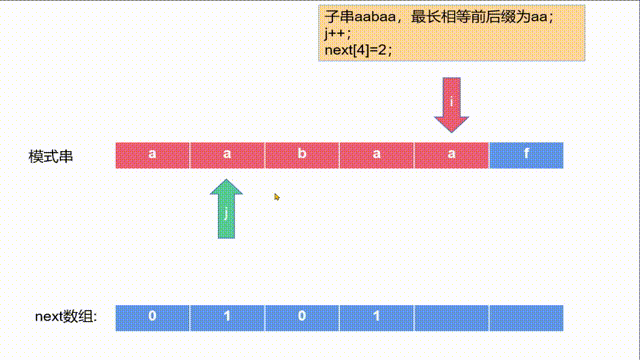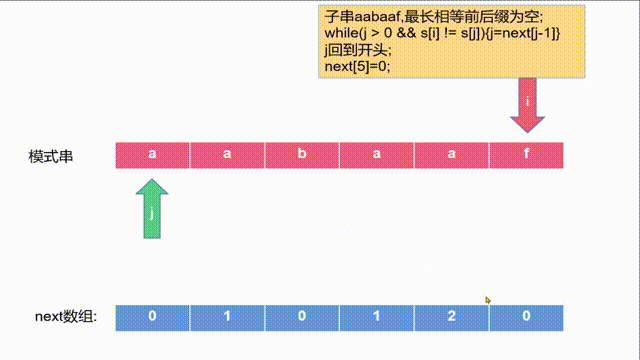
接着我们使用next数组进行匹配，如下图动画所示:

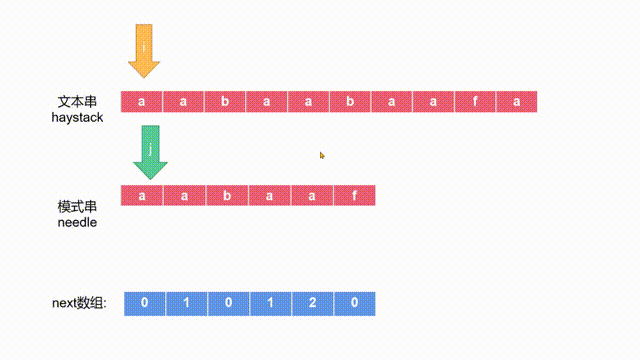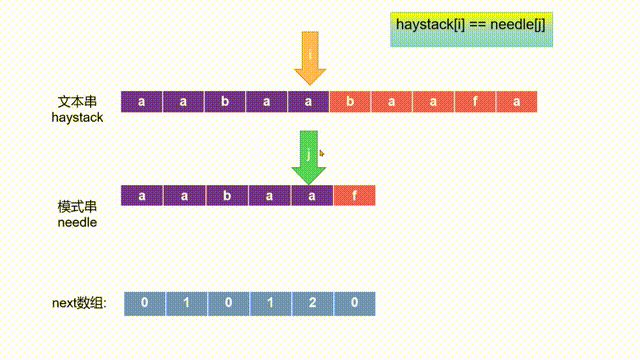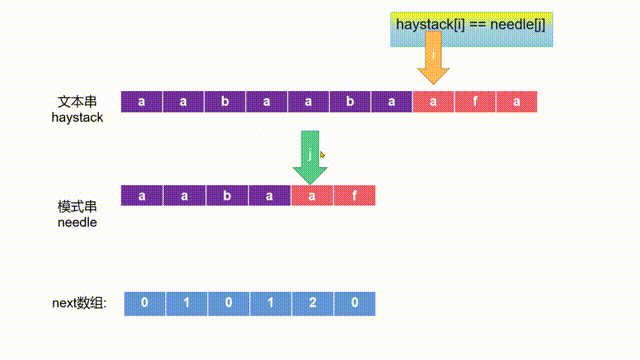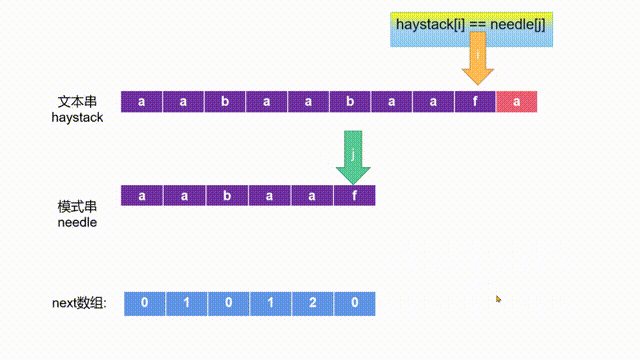
当文本串与模式串对应位置的字符不匹配了，我们需要调整模式串的位置，继续进行匹配。如下两图所示:

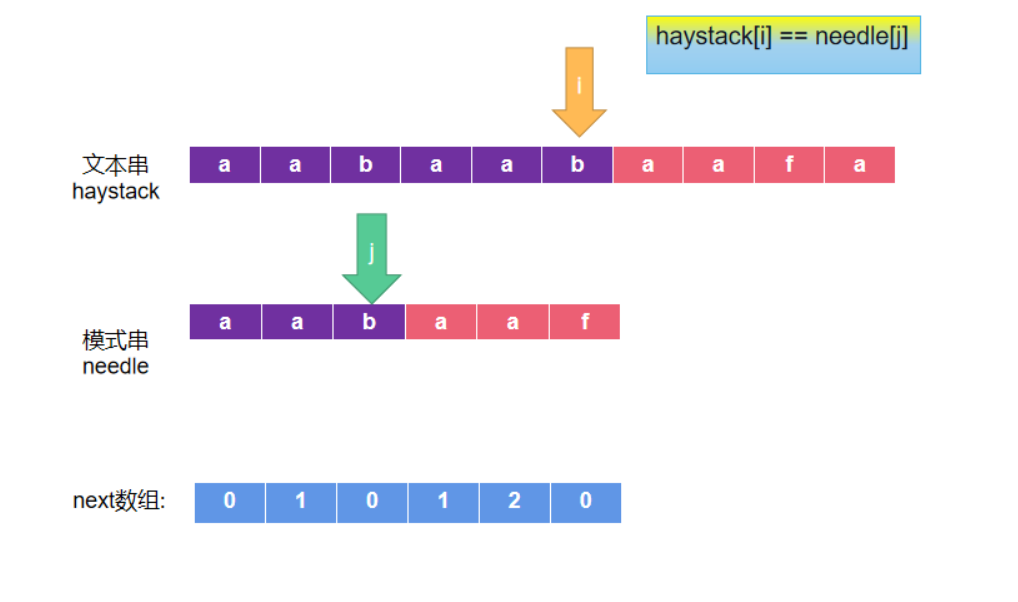
上图中当b f不匹配的时候，就往前回退，next[j-1]=2，说明后缀有aa,前面还有个与其相等的前缀aa，所以跳到b，继续匹配。
- 这就是——利用已经匹配过的内容，继续匹配。

全部代码如下:

class Solution {
public:
    void getNext(int* next,const string s){
        int n = s.size();
        int j = 0;
        next[0] = 0;
        // i 为前缀末尾
        // j 为后缀末尾
        for(int i = 1; i < n ;i++){
            while(j > 0 && s[i] != s[j]){// 控制回退，最多回退到开头，即j=0
                j = next[j-1];
            }
            if(s[i] == s[j])j++;
            next[i] = j;
        }
    }
    //  本题中next数组的求与使用很相似。
    int strStr(string haystack, string needle) {
        int next[needle.size()];
        // j负责遍历模式串
        // i负责遍历文本串
        getNext(next,needle);
        int j = 0;
        for(int i = 0;i < haystack.size();i++){
            // 当前这个字符不同，通过移动j指针指向的模式串位置，来调整继续匹配的位置。
            while(j > 0 && haystack[i] != needle[j]){
                j = next[j-1];
            }
            if(haystack[i] ==  needle[j])j++;
            if(j == needle.size()){
                return i-needle.size()+1;
            }

        }
        return -1;
    }
};

示例2: 459. 重复的子字符串
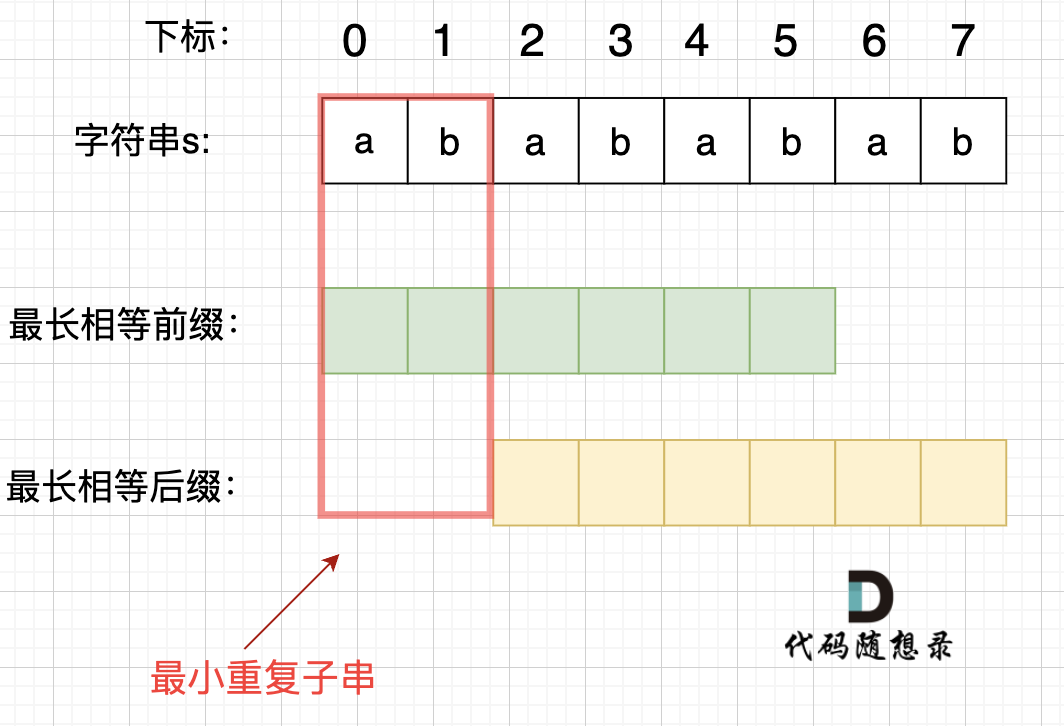
重复的子串的最小单位，就是字符串中最长相等前后缀所不包含的那个一个子串。
- 实际操作中，字符串的长度，减去最长相等前后缀的长度，即重复子串最小重复的单位的长度。
- 这一块(最小重复单位)的长度如果能被字符串的长度整除，说明该字符串是由重复的子串构成的。
  - 即，数组长度减去最长相同前后缀的长度相当于是第一个周期的长度，也就是一个周期的长度，如果这个周期可以被整除，就说明整个数组就是这个周期的循环。
  - 相关数学证明这里不做赘述，而且我也不想去深究这个，详见《代码随想录》-重复的子字符串
- 如下图所示:

举两个字符串的例子:
- asdfasdf
  - next数组: 0 0 0 0 1 2 3 4
- abababab
  - next数组: 0 0 1 2 3 4 5 6

class Solution {
public:
    void getNext(int* next,const string& s){
        int j = 0;
        next[0] = 0;
        for(int i =1; i < s.size();i++){
            while(j > 0 && s[i] != s[j]){
                j = next[j-1];
            }
            if(s[i] == s[j])j++;
            next[i] = j;
        }
    }
    bool repeatedSubstringPattern(string s) {
        if(s.size() == 0)return false;
        int next[s.size()];
        getNext(next,s);
        int len = s.size();
        // next[len-1] == 0就说明，以整体为子串的最长相等前后缀为0。
        // 如果是通过某一子串重复得到的，以整体为子串的最长相等前后缀不会为0。
        // 最小重复单位如果能被字符串的长度整除，说明该字符串是由重复的子串构成的。
        if(next[len-1] != 0 && len % (len-(next[len-1])) == 0)return true;
        return false;
    }
};