嵌入式基础知识-RSA非对称加密基本原理

1 RSA算法基本原理

RSA加密算法是由罗纳德·李维斯特（Ronald Linn Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德尔曼（Leonard Adleman）于1977年共同发明的。它的密钥计算规则可由下图所示。

公钥和私钥的基本特点为：

• 公钥和私钥中都有两个数字构成，并且其中一个数字是相同的，即图中所示的N，示例为33
• 公钥有自己特有的数字，即图中所示的E，示例为3
• 私钥有自己特有的数字，即图中所示的D，示例为7

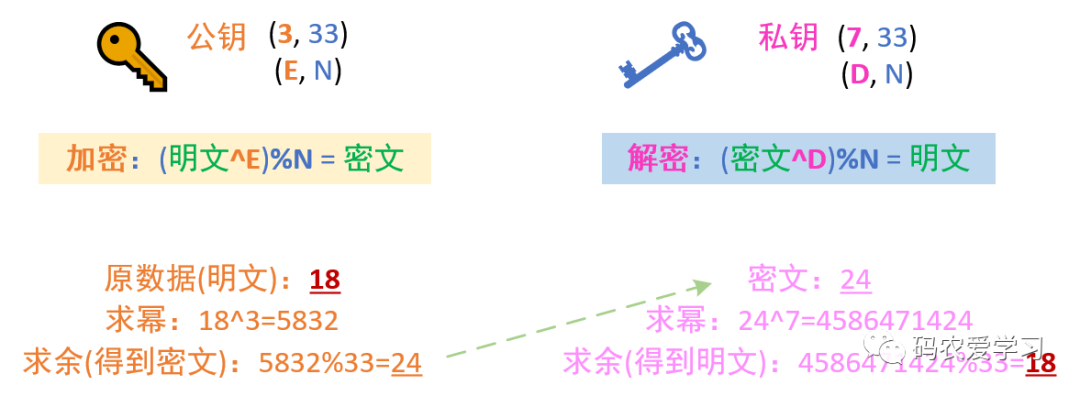
公钥加密的过程为（对明文中的每个字符分别解密，示例为加密其中一个字符）：

• 先对明文求E次幂
• 再将结果对N取余

私钥解密的过程与加密过程类似：

• 先对密文求D次幂
• 再将结果对N取余

2 RSA密钥计算规则

上面介绍了RSA加密解密的基本过程，那RSA的密钥（公钥和私钥），怎么计算得到呢？

RSA的密钥计算，需要用到质数和欧拉函数的知识。

质数的概念如果忘了，后面会再介绍。

欧拉函数暂不展开讲解，记住公式即可。

下面就来看下RSA密钥的计算步骤。

2.1 计算步骤

RSA密钥（公钥和私钥）的计算步骤可分为如下五步：

• 第一步：取两个质数，如p=3，q=11
• 第二步：质数相乘，N=pxq=3x11=33
• 第三步：欧拉函数，T=(p-1)x(q-1)=2x10=20
• 第四步：选公钥E，需满足以下条件： 可以从小开始选，选E=3，因此公钥为(3, 33)
  • 是一个质数
  • 1<公钥<T
  • 不是T的因子
• 第五步，计算私钥D，公式为**(DxE)%T=1**，解得D=7，因此私钥为(7,33)

RSA密钥的计算规则是公开的，那破译的难点在哪里呢？

其实，在实际使用时，两个质数尽量取大，转换成二进制后1024个二进制位或者更多，位数越多越难破解。

对于RSA的破解难度分析：

• 公钥(E，N)是公开的，要想破解密钥，就是求出D
• 根据公式(DxE)%T=1，E是已知的，下一步就是要获取到T，而T=(p-1)x(q-1)，与两个质数有关
• 虽然N=pxq，N也是已知的，但如果这两个质数设置的非常大，N和T也就会很大
• 而对于大数的质数分解，是很难计算的，这就是RSA算法难破解的原理了

2.2 质数简介

上面说到，RSA密钥的计算，需要用的质数，那质数的概念，是否还熟悉呢？

质数是小学数学中就学过的知识点，不过平时用的不多，这里再简单回顾以下。

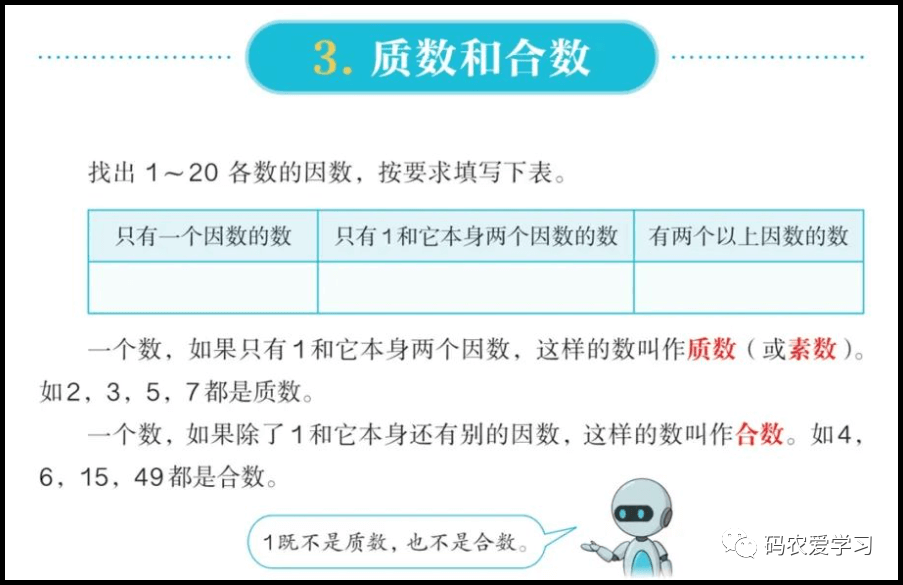
质数（也叫素数），指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。

质数的一些性质：

• 质数p的约数只有两个：1和p
• 算术基本定理：任一大于1的自然数，要么本身是质数，要么可以分解为几个质数之积，且这种分解是唯一的
• 质数的个数是无限的
• 若n为正整数，在n^2到(n+1)^2之间至少有一个质数
• 若n为大于等于2的正整数，在n到n!之间至少有一个质数

可以写一段代码，求取一定范围的质数，感受一下质数有哪些。

代码怎么写呢？还是可以看下小学课本：

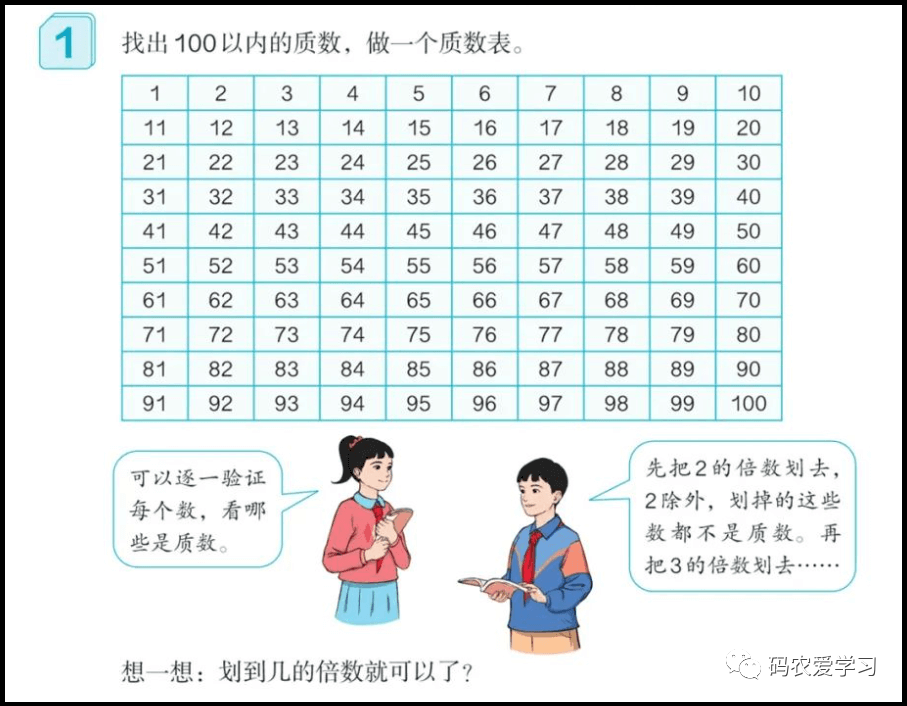
用Python编写的打印5000以内质数的代码如下：

#判断是否是质数：大于1，不等于2，是否为奇数，是否有约数'''
def isPrime(num):
    if num > 1:
        if num>2:
            if num%2==1:
                for i in range(2, int((num-1)/2)): 
                    if num%i == 0:
                        return False #有约数
                return True #无约数
            return False #3以上的偶数
        return True #等于2
    return False #小于2

if __name__ == '__main__':
    prime_list = []
    for i in range(5000):
        if isPrime(i):
            prime_list.append(i)
    print(prime_list)

这里列举5000以内的质数：

3 RSA密钥计算实例

题目：RSA算法中，选择两个质数，p=11，q=17，加密密钥为e=23，且求解密密钥。

分析：按照RSA算法的基本原理，N=pxq=11x17=187，T=(p-1)x(q-1)=10x16=160，而E=23，

根据(DxE)%T=1，即(Dx23)%160=1，解得D=7

4 总结

本篇介绍了RSA这种非对称加密算法的加密解密基本过程，以及公钥和私钥的计算基本步骤，并补充介绍了质数的相关概念，最后通过一个实例来简单体会下RSA密钥的计算。