一文理解kmp算法（java代码）

用户10604450

发布于 2024-03-15 14:27:51

3550

文章被收录于专栏：练习两年半练习两年半

kmp是为了解决什么问题？

字符串匹配问题，用来在主字符串中查找匹配字符串的位置

N, M ：字符串的长度 char s[N], p[M]：待匹配串匹配串 eg: s[N] = “ababa”, p[M] = “aba” 判断 s[N] 中是否有p[M]这个子串，如果有，开始下标为多少?

解决方法

暴力算法

   for(int i = 1; i <= n; i++) {
    bool flag = true;
    for(int j = 1; j <= m；j++) {
        if(s[i+j-1] != p[j]) {
            flag = false;
            break;
         }         
      }
   }

时间复杂度：O(n*m)

kmp优化

对于模式串中已经匹配过的那些字符，如果我们能找到一些规律，将模式串多往后移动几位，而不是像暴力算法算法一样，每次把模式串移动一位，就可以提高算法的效率。kmp算法给我们提供的思路是：对于模式串，将每一个字符在匹配失败时可以向后移动的最大距离保存在一个next数组。这样当匹配失败时就可以按照next数组中保存的数字向后多移动几位。从而提高算法的效率。

在讲述之前，我们先摆出两个概念：

前缀：指的是字符串的子串中从原串最前面开始的子串，如abcdef的前缀有：a,ab,abc,abcd,abcde 后缀：指的是字符串的子串中在原串结尾处结尾的子串，如abcdef的后缀有：f,ef,def,cdef,bcdef

什么是前缀数组next[]

在KMP算法中有个关键的数组，叫做前缀数组，每一个子串有一个固定的next数组，它记录着字符串匹配过程中失败情况下可以向后多跳几个字符，其实也是子串的前缀和后缀相同的最长长度。

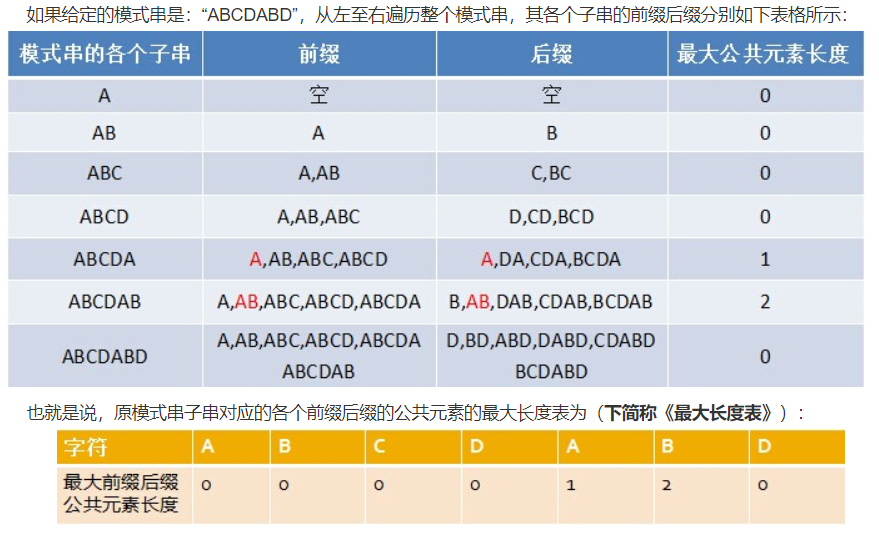
怎么求这个数组我们放在最后说，先说怎么使用这个前缀数组来实现kmp算法

算法思路

思路其实已经说过了，就是在暴力的算法的基础上，在匹配失败的时候往后多跳几位，而跳几位保存在前缀数组中。接下来我们看一下原理是什么样的，为什么前缀数组就可以作为跳几步的依据。举个例子，下图中已经写好了总串s和模式串p,模式串的前缀数组为[0,0,1,2,3],且所以下标都是从1开始。看图中当i=8，j=4时s[i] != p[j + 1]，即将要匹配失败了，图中红色圈住的是子串的后缀。黄圈圈住的是前缀。蓝色圈圈住的是已经和后缀匹配过的部分，那么下一次将模式串后移prefix[j]=2位时，原来的前缀正好对着蓝色圈圈部分，因为前缀=后缀=蓝色圈圈部分，所以移动后的橙色部分就不用再判断了。

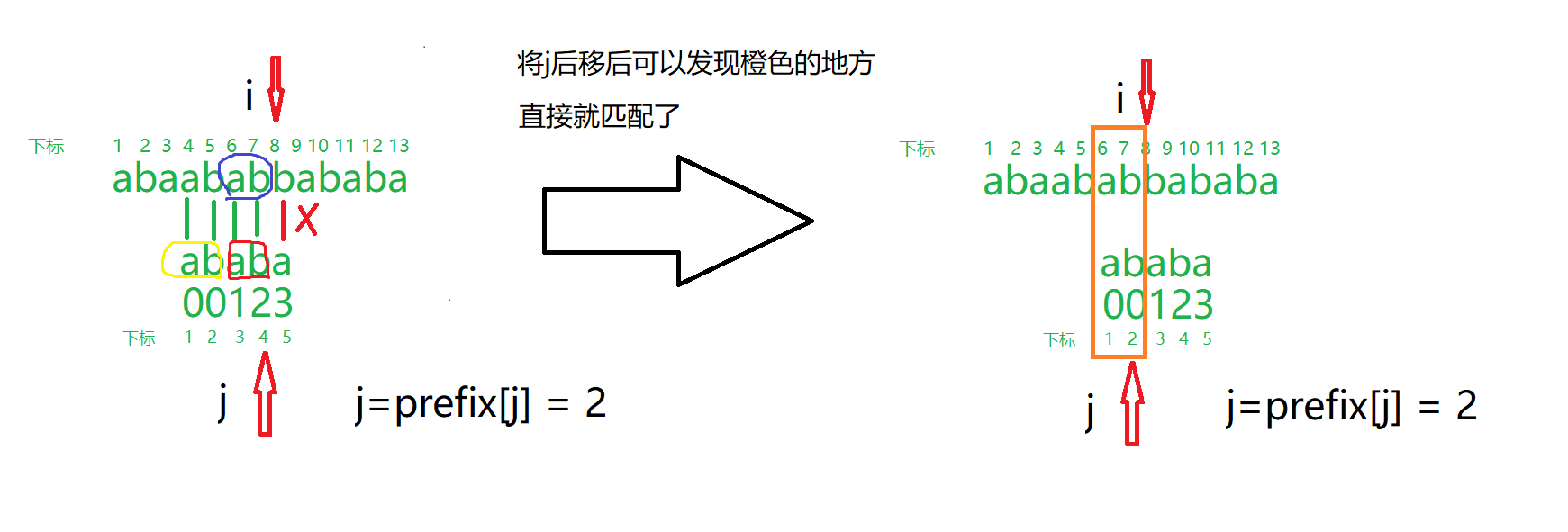
再用上一个双指针算法思路。i遍历总串s，j遍历模式串p，判断s[i] 和 p[j + 1]是否匹配。不匹配就将j重置为前缀数组中prefix[j]的值。匹配的话j忘后移动一位。当匹配了n个字符后即代表完全匹配。此时答案即为i-n，如果要继续搜索，要将j再置为prefix[j]。

为了方便写代码所有数组的下标都从1开始

// kmp匹配
for (int i = 1, j = 0; i <= m; i++) {
    while (j != 0 && s[i] != p[j + 1]) {
        j = prefix[j]; // s[i] != p[j + 1]即不匹配，则往后移动
    }
    if (s[i] == p[j + 1])
        j++; // 匹配时将j++进行下一个字符的匹配
    if (j == n) { 
        j = prefix[j]; // 完全匹配后继续搜索
        System.out.print(i - n + " ");
    }
}

怎么求前缀数组

前缀数组是kmp里面最难的部分，网上也有很多种求法。比如利用后一个元素和前面的元素之间存在数学公式关系来求，我们这里使用的方式是和上面的匹配过程类似的方法，也就是将前缀看作模式串，在p中匹配他。也就是字符串p自己找自己的匹配串。

完整代码

import java.io.*;

public class Main {
    static int N=100010;
    static int M=1000010;
    static char []p=new char[N];
    static int []ne=new int[N];
    static char []s=new char[M];
    public static void main(String[] args) throws IOException {
        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw=new BufferedWriter(new OutputStreamWriter(System.out));

        int n=Integer.parseInt(br.readLine());
        String s1= br.readLine();
        for (int i = 1; i <=n; i++) {
            p[i]=s1.charAt(i-1);
        }
        int m=Integer.parseInt(br.readLine());
        String s2= br.readLine();
        for (int i =1; i <=m; i++) {
            s[i]=s2.charAt(i-1);
        }
        //构建前缀数组ne[]
        for(int i=2,j=0;i<=n;i++){
            while (j!=0 && p[i]!=p[j+1]) j=ne[j];
            if(p[i]==p[j+1]) j++;
            ne[i]=j;
        }
        //kmp匹配
        for(int i=1,j=0;i<=m;i++){
            while (j!=0 && s[i]!=p[j+1]) j=ne[j];
            // 匹配时将j++进行下一个字符得匹配
            if(s[i]==p[j+1]) j++;
            if(j==n){
                //当匹配成功时继续往下匹配
                j=ne[j];
                bw.write(i-n+" ");
            }
        }
        bw.flush();
        br.close();
        bw.close();
    }
}

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2023-01-08，如有侵权请联系 cloudcommunity@tencent.com 删除

数组