【数据结构与算法】二叉树的非递归遍历算法实现详解(常见面试题)
【数据结构与算法】二叉树的非递归遍历算法实现详解(常见面试题)

利刃大大
发布于 2025-02-03 08:12:36
发布于 2025-02-03 08:12:36
代码可运行
运行总次数:0
代码可运行
二叉树进阶面试题
- 二叉树创建字符串
- 二叉树的分层遍历1
- 二叉树的分层遍历2
- 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先
- 二叉树搜索树转换成排序双向链表
- 根据一棵树的前序遍历与中序遍历构造二叉树
- 根据一棵树的中序遍历与后序遍历构造二叉树
- 二叉树的前序遍历,非递归迭代实现
- 二叉树中序遍历 ,非递归迭代实现
- 二叉树的后序遍历 ,非递归迭代实现
这里我们主要讲一下迭代版本的前中后序遍历,其他的放到刷题笔记中去!
1、迭代实现前序遍历
首先讲讲为什么要去实现非递归的遍历呢,因为递归的缺陷就是空间问题,栈溢出是有可能存在的情况,所以我们必须尝试着去迭代遍历!
回归正题!我们怎么实现迭代遍历呢?还能像递归一样递归左右子树吗,显然不太行!所以我们这里又给了一个新思路:
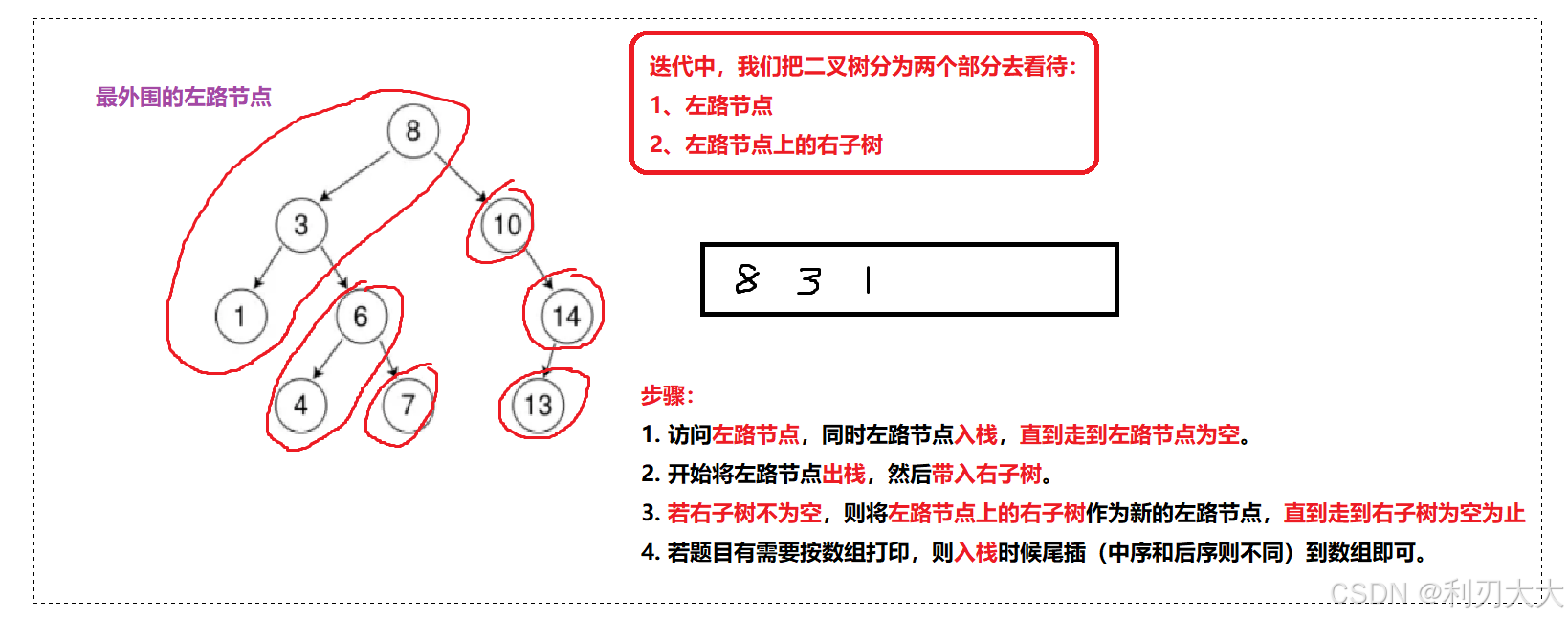
将二叉树分为两个部分去看待:
- 左路节点
- 左路节点上的右子树
然后借用 栈 来模拟递归
前序遍历步骤:
- 访问左路节点,同时左路节点入栈,直到走到左路节点为空。
- 开始将左路节点出栈,然后带入右子树。
- 若右子树不为空,则将左路节点上的右子树作为新的左路节点,直到走到右子树为空为止
- 若题目有需要按数组打印,则 入栈时候尾插(中序和后序则不同) 到数组即可。
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> v;
TreeNode* cur = root;
// 当cur为空且st为空说明已经遍历完了
while(cur || !st.empty())
{
// 1、访问左路节点,左路节点入栈
while(cur != nullptr)
{
st.push(cur);
v.push_back(cur->val);
cur = cur->left;
}
// 2、依次取左路节点的右子树出来访问
TreeNode* top = st.top();
st.pop();
cur = top->right;
}
return v;
}
};2、迭代实现中序遍历
有了前序遍历做铺垫就好理解了,中序也就是在前序的基础上改动了一点!
与前序不同的是:
- 中序不能在入左路节点进栈的时候进行打印或者尾插节点元素(因为中序得先访问左子树再访问中间节点!)
- 所以中序得在左路节点都入栈后才打印或者尾插节点元素
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> v;
TreeNode* cur = root;
while(cur || !st.empty())
{
// 1、先将左路节点入栈
while(cur != nullptr)
{
st.push(cur);
cur = cur->left;
}
// 依次取左路节点的右子树进行访问
// 与前序遍历不同,中序在左路节点全部入栈、访问右子树之前顺便打印或者尾插该节点
TreeNode* top = st.top();
st.pop();
v.push_back(top->val);
cur = top->right;
}
return v;
}
};3、迭代实现后序遍历
后序的情况就相对来说比较复杂啦,但是大体的思路还是和前中序是差不多的!
思路:
- 与前中序一样,先将左路节点都入栈
- 然后依次取左路节点的右子树出来访问
- 如果这个时候右子树为空或者右子树已经访问过了,那么就可以访问栈顶元素了
- 如果这个时候右子树不为空且还没被访问过,那就让
cur = top->right变成子问题去解决
而这里面最重要的一点就是如何让右子树已经知道自己被访问过了?
💡 我们可以设一个 flag 变量,然后将每次出栈的元素赋给 flag,当我们用 top 去访问右子树的时候,每次就看看 top->right == flag,若相等则说明刚才已经遍历过了,若没有的话就遍历右子树!
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> v;
TreeNode* cur = root;
TreeNode* flag = nullptr; //用来标记是否走过该右子树的节点
while(cur || !st.empty())
{
// 1、访问左路节点,左路节点入栈
while(cur != nullptr)
{
st.push(cur);
cur = cur->left;
}
// 2、依次取左路节点的右子树出来访问
TreeNode* top = st.top();
//若右子树为空或者右子树已经访问过了(top->right == flag),那么我们就可以访问栈顶元素了
if(top->right == nullptr || top->right == flag)
{
st.pop();
v.push_back(top->val);
flag = top; //将top该点赋给flag,说明该点是走过的了
}
else
{
cur = top->right;
}
}
return v;
}
};本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2025-01-28,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

