【算法/学习】：搞懂链表题型，这一篇就够了

IsLand1314

发布于 2025-02-25 14:08:41

12000

代码可运行

文章被收录于专栏：学习之路学习之路

运行总次数：0

代码可运行

一、知识培训

链表（Linked List） 是一种线性数据结构，由一系列节点组成。每个节点包含两个部分：

数据域：存储实际数据。
指针域：指向下一个节点的地址（在双向链表中还会指向前一个节点）。

链表通过指针将零散的内存块串联起来，支持动态内存分配，插入和删除操作高效，但随机访问效率低。常见的链表类型包括：

单向链表：每个节点仅指向下一个节点
双向链表：节点同时指向前驱和后继
循环链表：尾节点指向头节点形成环

🐇 特性

链表的核心特性决定了其适用场景和操作方式：

动态内存分配
- 链表节点在内存中非连续分布，可以动态扩展或收缩，适合数据规模不确定的场景。
- 对比数组：数组需要预先分配连续内存，扩容成本高。
高效的插入和删除
- 时间复杂度：O(1)（已知前驱节点）或 O(n)（需遍历查找位置）。
- 对比数组：数组插入/删除需移动元素，时间复杂度 O(n)。
低效的随机访问
- 访问第 k 个元素需从头遍历，时间复杂度 O(n)。
- 对比数组：数组通过下标直接访问，时间复杂度 O(1)。

🐇 解题关键：指针操作与技巧

链表问题的核心是指针操作，需灵活处理节点之间的指向关系。常见技巧如下：

1. 虚拟头节点（Dummy Node）

作用：起到了一个哨兵的作用，简化边界处理（如删除头节点、合并链表）
示例：合并两个有序链表时，用虚拟头节点统一操作逻辑，具体题目：21. 合并两个有序链表 - 力扣（LeetCode）

ListNode* dummy = new ListNode(0);  // 虚拟头节点
ListNode* cur = dummy;
while (l1 && l2) {
    if (l1->val <= l2->val) {
        cur->next = l1;
        l1 = l1->next;
    } else {
        cur->next = l2;
        l2 = l2->next;
    }
    curr = curr->next;
}
if(l1) cur->next = l1;
if(l2) cur->next = l2;

2. 双指针技巧

快慢指针：解决环检测、中间节点、倒数第 k 节点等问题。具体题目：141. 环形链表 - 力扣（LeetCode）

 // 检测链表是否有环
 ListNode* slow = head, *fast = head;
 while (fast && fast->next) {
     slow = slow->next;
     fast = fast->next->next;
     if (slow == fast) return true;
 }
 return false;

前后指针：用于反转链表、删除节点等。具体题目：LCR 024. 反转链表 - 力扣（LeetCode）

 // 反转链表
 ListNode* prev = nullptr, *cur = head;
 while (cur) {
     ListNode* next = cur->next;
     cur->next = prev;
     prev = cur;
     cur = next;
 }
 return prev;

3. 递归与迭代

递归：适用于反向操作（如反向打印链表、反转链表）具体题目：LCR 024. 反转链表 - 力扣（LeetCode）

 // 递归反转链表
 ListNode* reverseList(ListNode* head) {
     if (!head || !head->next) return head;
     ListNode* newHead = reverseList(head->next);
     head->next->next = head; // 相当于儿子的下一个儿子指向自己 A->B ==> A<-B 
     head->next = nullptr;
     return newHead;
 }

迭代：更节省栈空间，适合大规模数据。

实战技巧

画图分析：在纸上画出链表结构和指针变化，避免逻辑错误（链表中画图是非常重要的）

边界检查：处理头节点、尾节点、空链表等情况

断链保护：修改指针前记录后续节点，防止丢失链表

ListNode* next = curr->next;  // 先保存下一个节点
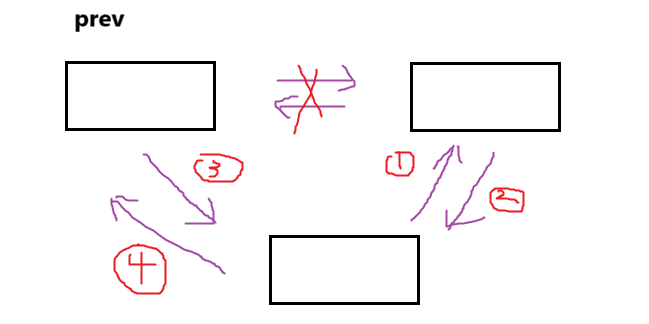
curr->next = prev;            // 再修改当前指针

插入节点：在两个双向链接节点之间插入一个节点（这个经常考选择填空），注: 已知 prev 是左节点，cur 是要插入节点

prev->next->prev = cur;
cur->next = prev->next;
prev->next = cur; 
cur->prev = prev;

画图如下：

🐇补充内容：链表的进阶技巧与扩展应用

1. 复杂链表的处理技巧

链表的进阶问题通常涉及 复杂指针操作 或 特殊结构，需结合其他算法思想（如分治、哈希、栈等）解决。以下是补充内容：

1.1 链表排序

问题场景：对无序链表进行排序（如时间复杂度 O(nlogn) 的排序）具体题目：LCR 077. 排序链表 解决策略：

归并排序：利用快慢指针找到中点，分割链表后递归合并（相当于变成了合并两个链表了）

ListNode* sortList(ListNode* head) {
    if (!head || !head->next) return head;
    ListNode* slow = head, *fast = head->next;
    while (fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
    }
    ListNode* mid = slow->next;
    slow->next = nullptr;  // 切断链表
    return merge(sortList(head), sortList(mid));
}

ListNode* merge(ListNode* l1, ListNode* l2) {
    ListNode dummy(0), *curr = &dummy;
    while (l1 && l2) {
        if (l1->val <= l2->val) {
            curr->next = l1;
            l1 = l1->next;
        } else {
            curr->next = l2;
            l2 = l2->next;
        }
        curr = curr->next;
    }
    curr->next = l1 ? l1 : l2;
    return dummy.next;
}

1.2 合并 K 个有序链表

问题场景：高效合并多个有序链表。具体题目：LCR 078. 合并 K 个升序链表 解决策略：

优先级队列（最小堆）：将每个链表的头节点入堆，每次取出最小值。

struct cmp {
    bool operator()(ListNode* a, ListNode* b) {
        return a->val > b->val;  // 最小堆
    } 
};

ListNode* mergeKLists(vector<ListNode*>& lists) {
    priority_queue<ListNode*, vector<ListNode*>, cmp> pq;
    for (auto list : lists) {
        if (list) pq.push(list);
    }
    ListNode dummy(0), *curr = &dummy;
    while (!pq.empty()) {
        ListNode* node = pq.top();
        pq.pop();
        curr->next = node;
        curr = curr->next;
        if (node->next) pq.push(node->next);
    }
    return dummy.next;
}

当然我们也有第二种方法，递归到合并两个有序链表即可，代码如下：

ListNode* mergeKLists(vector<ListNode*>& lists) {
        return merge(lists, 0, lists.size() - 1);
    }
    ListNode *merge(vector<ListNode*> &lists, int l ,int r)
    {
        if(l > r) return nullptr;
        if(l == r) return lists[l];

        // 1. 平分数组
        int mid = (l + r) >> 1;
        // [l, mid] [mid + 1, r]

        // 2. 递归处理左右区间
        ListNode* l1 = merge(lists, l, mid);
        ListNode* l2 = merge(lists, mid + 1, r);

        // 3. 合并两个有序链表
        return mergeTwoList(l1, l2);
    }
    ListNode *mergeTwoList(ListNode* l1, ListNode* l2)
    {
        ListNode* dummy = new ListNode(0);
        ListNode* cur = dummy;
        while(l1 && l2){
            if(l1->val < l2->val){
                cur->next = l1;
                l1 = l1->next;
            }
            else{
                cur->next = l2;
                l2 = l2->next;
            }
            cur = cur->next;
        }
        if(l1) cur->next = l1;
        if(l2) cur->next = l2;
        return dummy->next;
    }

1.3 深拷贝带随机指针的链表

问题场景：复制一个链表，其中每个节点包含 random 指针，可能指向任意节点或 nullptr，具体题目：138. 随机链表的复制 解决策略：

哈希表映射：存储原节点到新节点的映射，分两次遍历处理 next 和 random。

Node* copyRandomList(Node* head) {
    if (!head) return nullptr;
    unordered_map<Node*, Node> old2new;
    Node* curr = head;
    // 第一遍：创建新节点并建立映射
    while (curr) {
        old2new[curr] = new Node(curr->val);
        curr = curr->next;
    }
    // 第二遍：处理 next 和 random
    curr = head;
    while (curr) {
        old2new[curr]->next = old2new[curr->next];
        old2new[curr]->random = old2new[curr->random];
        curr = curr->next;
    }
    return old2new[head];
}

2. 内存管理与优化

链表操作需特别注意 内存安全，尤其在 C/C++ 中。以下是关键点：

2.1 内存泄漏预防

手动释放内存：删除节点后需显式释放内存。

void deleteList(ListNode* head) {
    while (head) {
        ListNode* temp = head;
        head = head->next;
        delete temp;  // 释放节点内存
    }
}

2.2 避免悬挂指针

置空指针：删除节点后，将指向它的指针设为 nullptr。

 ListNode* prev = ...; 
 ListNode* toDelete = prev->next;
 prev->next = toDelete->next;  // 跳过待删除节点
 delete toDelete;
 toDelete = nullptr;  // 防止误用

3. 链表的扩展结构

链表可通过变体解决更复杂的问题：

3.1 跳表（Skip List）

特性：多层链表结构，支持 O(logn) 时间复杂度的查找、插入、删除。
应用场景：Redis 的有序集合（Sorted Set）底层实现。

3.2 十字链表（Orthogonal List）

特性：用于表示稀疏矩阵，每个节点同时属于行链表和列链表。
结构：包含行指针、列指针、数据域。

4. 链表与其他数据结构的结合

链表常作为其他复杂数据结构的底层实现：

4.1 哈希链表（LinkedHashMap）

特性：哈希表 + 双向链表，实现 O(1) 时间复杂度的插入、删除、访问，并维护插入顺序。
应用场景：LRU 缓存淘汰算法。

4.2 链式栈/队列

实现方式：用链表头作为栈顶或队列头，支持动态扩容。

 // 链式栈
 class LinkedStack {
 private:
     ListNode* top;
 public:
     void push(int val) {
         ListNode* node = new ListNode(val);
         node->next = top;
         top = node;
     }
     int pop() {
         if (!top) throw "Empty Stack";
         int val = top->val;
         ListNode* temp = top;
         top = top->next;
         delete temp;
         return val;
     }
 };

5. 实战避坑指南

常见错误	解决方法
未处理空指针（如 head 为空）	所有操作前检查指针是否为 nullptr
指针丢失导致内存泄漏	修改指针前保存后续节点（如 ListNode* next = curr->next）
循环引用导致死循环	在遍历链表时记录已访问节点（如使用哈希表检测环）
双向链表未同步更新前后指针	插入或删除节点时，同时修改前驱和后继节点的指针

6. 何时选择链表？

场景	推荐数据结构	理由
频繁在头部/中部插入或删除	链表	O(1) 或 O(n) 时间，无需移动元素
数据规模动态变化	链表	动态内存分配，无扩容成本
需要实现 LRU 缓存	哈希链表	快速访问 + 维护顺序
需要快速随机访问（如二分查找）	数组	O(1) 时间访问任意位置

通过掌握上述进阶技巧和扩展知识，可以更高效地解决复杂链表问题，并理解其在系统设计中的实际应用价值。

二、其余题目训练

1. 找到环形链表的入口点

具体题目：LCR 022. 环形链表 II

题目描述：

给定一个链表，返回链表开始入环的第一个节点。从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。

示例：

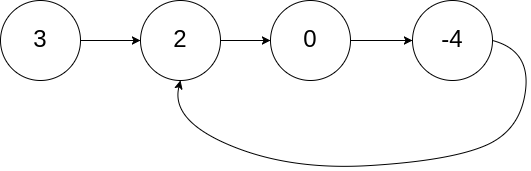
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

思路：

这个题目的话，我们仍然需要用到快慢指针的思路，然后基于快慢指针先判断当前是否有环，然后当两个指针在环中相遇的时候，会出现如下情况：

此时我们可以知道当两者相遇时，fast 假设已经走完环的 n 圈，则走过总距离为 x + d + n *m
而且由于任意时刻 fast 指针走过距离是 slow 指针 2 倍，因此有：x + d + n *m = 2 * (x + d)
因此可以推出：x = m - d + (n - 1) * m，我们会发现：从相遇点到入环点的距离加上n−1圈的环长，恰好等于从链表头部到入环点的距离。
因此，当发现slow与fast相遇时，我们再额外使用一个指针ptr。起始，它指向链表头部；随后，它和slow每次向后移动一个位置。最终，它们会在入环点相遇。

代码如下：

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head, *fast = head;
        while(!fast && !fast->next){
            slow = slow->next;
            fast = fast->next->next;
            if(slow == fast){ // 表示有环
                slow = head; //这里直接把 slow 看作 ptr，让其回到原点即可
                while(slow != fast){
                    slow = slow->next;
                    fast = fast->next;
                }
                return slow;
            }
        }
        return nullptr;
    }
};

2. 两数相加

具体题目：2. 两数相加

题目描述：

给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例：

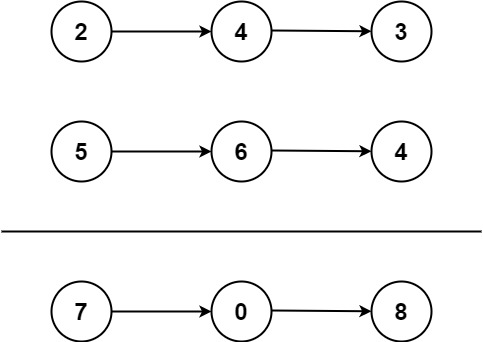
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

思路：

由于输入的两个链表都是逆序存储数字的位数的，因此两个链表中同一位置的数字可以直接相加。

我们同时遍历两个链表，逐位计算它们的和，并与当前位置的进位值相加。
具体而言，如果当前两个链表处相应位置的数字为n1,n2，进位值为carry，则它们的和为n1+n2+carry；
其中，答案链表处相应位置的数字为(n1+n2+carry) % 10，而新的进位值为⌊n1+n2+carry⌋ / 10。

如果两个链表的长度不同，则可以认为长度短的链表的后面有若干个0。此外，如果链表遍历结束后，有carry>0，还需要在答案链表的后面附加一个节点，节点的值为carry。

代码如下 ：

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* cur1 = l1, *cur2 = l2;
        ListNode* dummy = new ListNode(0); // 创建一个虚拟头节点，记录最终结果
        ListNode* cur = dummy;  // 尾指针
        int t = 0; // 进位
        while(cur1 || cur2 || t)
        {
            if(cur1) { // 先加上第一个链表
                t += cur1->val;
                cur1 = cur1->next; 
            }
            if(cur2) { // 再加上第二个链表
                t += cur2->val;
                cur2 = cur2->next; 
            }
            cur->next = new ListNode(t % 10);
            cur = cur->next;
            t /= 10;
        }

        cur = dummy->next;
        delete dummy; // new 之后需要释放
        return cur;
    }
};

3. 两两交换链表中的节点

具体题目：24. 两两交换链表中的节点

题目描述：

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）

示例：

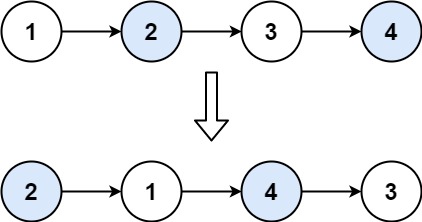
输入：head = [1,2,3,4]
输出：[2,1,4,3]

思路：

解法一：递归

解法二：迭代，用到了反转链表的想法

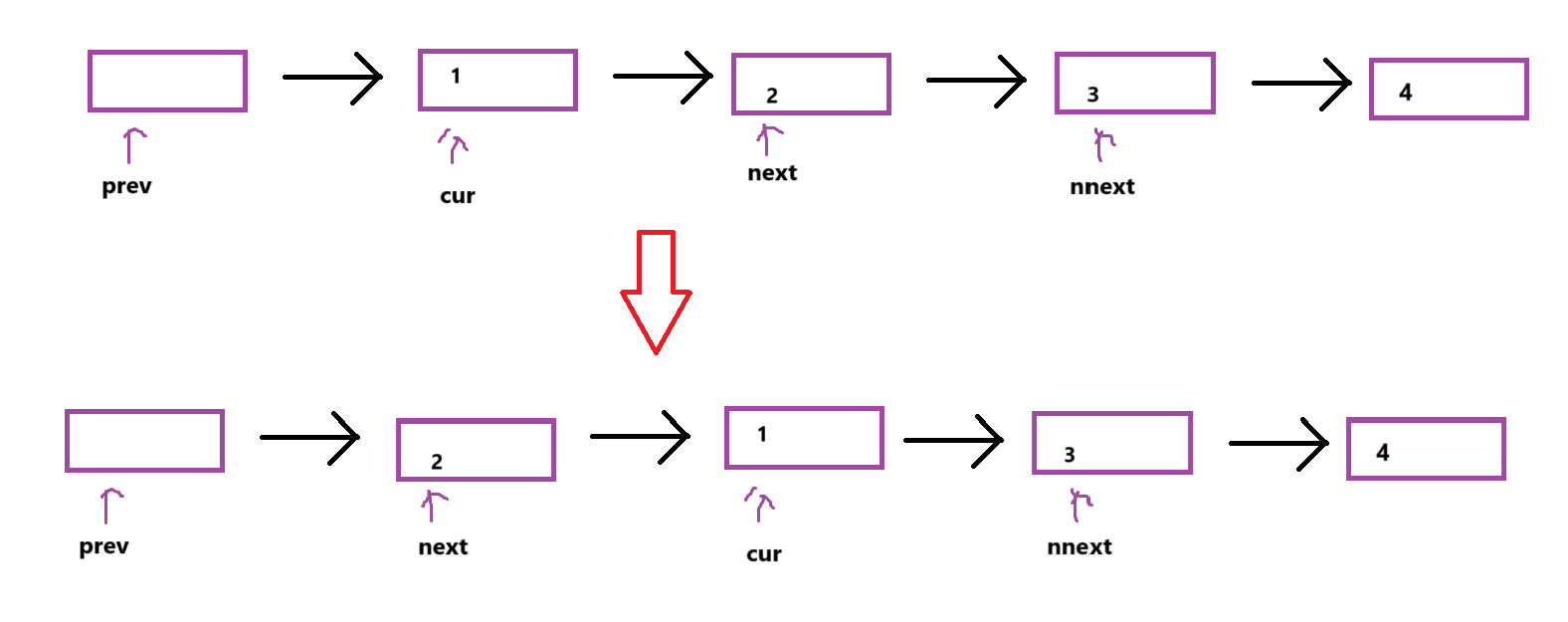
代码如下：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (head == nullptr || head->next == nullptr) return head;
        ListNode* newhead = new ListNode(0);
        newhead->next = head;

        ListNode* prev = newhead, *cur = prev->next, *next = cur ->next, *nnext = next->next;
        while(next && cur)
        {
            // 交换节点
            prev->next = next;
            next->next = cur;
            cur->next = nnext;

            // 修改指针
            prev = cur;
            cur = nnext;
            if(cur) next = cur->next;
            if(next) nnext = next->next;
        }
        return newhead->next;
    }
};

4. 删除链表倒数第 N 个节点

具体题目：19. 删除链表的倒数第 N 个结点

题目描述：

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例：

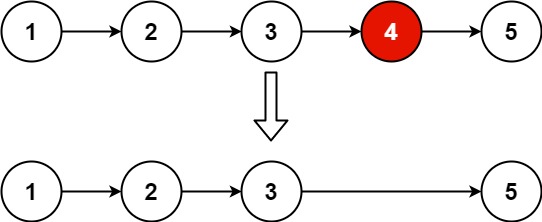
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

思路：统计长度往后走即可

代码如下：

class Solution {
public:
    int length(ListNode* head)
    {
        ListNode* cur = head;
        int len = 0;
        while(cur)
        {
            len++;
            cur = cur->next;
        }
        return len;
    }
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* cur = head;
        int len = length(head);
        int cnt = len - n - 1;
        if(cnt < 0) return cur->next;
        while(cnt--){
            cur = cur->next;
        }
        cur->next = cur->next->next;
        return head;
    }
};

5. k 个一组翻转链表

具体题目：25. K 个一组翻转链表

题目描述：

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例：

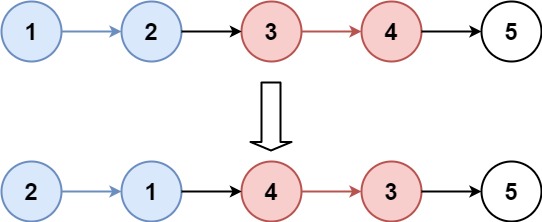
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

思路：

先求出需要逆序多少组： n
重复 n 次，长度为 k 的链表逆序即可（头插法）

代码如下：

class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        // 1. 先求出逆序多少组
        ListNode* cur = head;
        int n = 0;
        while(cur){
            cur = cur->next;
            n++;
        }
        n /= k;

        // 2. 对 n 个长度为 k 的链表进行翻转
        ListNode* newhead = new ListNode(0);
        ListNode* prev = newhead;
        cur = head;
        for(int i = 0 ; i < n; i++){
            ListNode* tmp = cur; // 记录下次头插的头节点
            for(int j = 0; j < k; j++){
                ListNode* next = cur->next;
                cur->next = prev->next;
                prev->next = cur;
                cur = next;
            }
            prev = tmp;
        }
        // 3. 把不需要的翻转接上
        prev->next = cur;

        cur = newhead->next;
        delete newhead;
        return cur;
    }
};

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-02-24，如有侵权请联系 cloudcommunity@tencent.com 删除

指针