动态规划（六）——简单多状态问题

用户11352420

发布于 2025-05-09 08:54:11

1300

文章被收录于专栏：编程学习编程学习

买卖股票的最佳时机含手续费

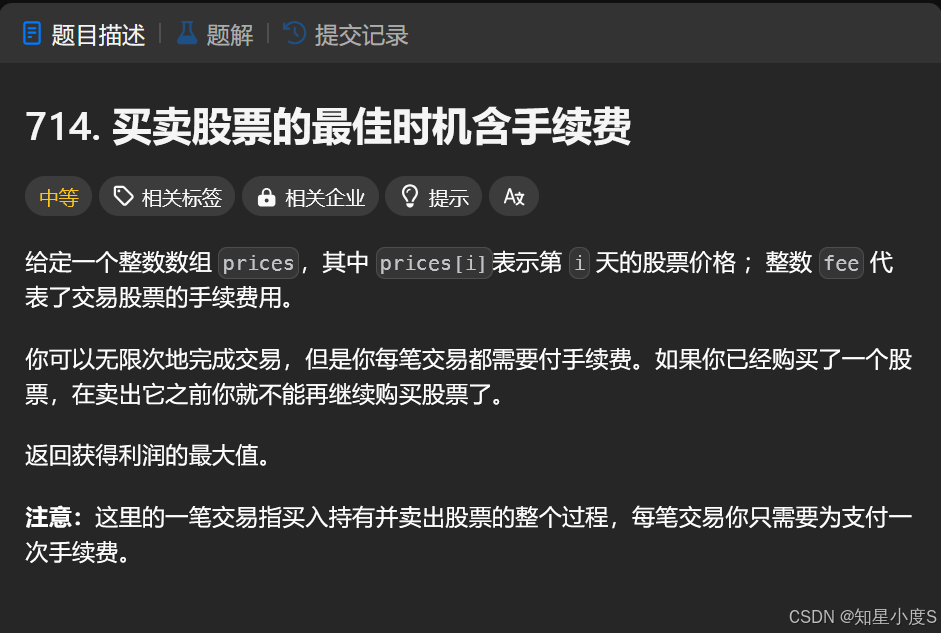
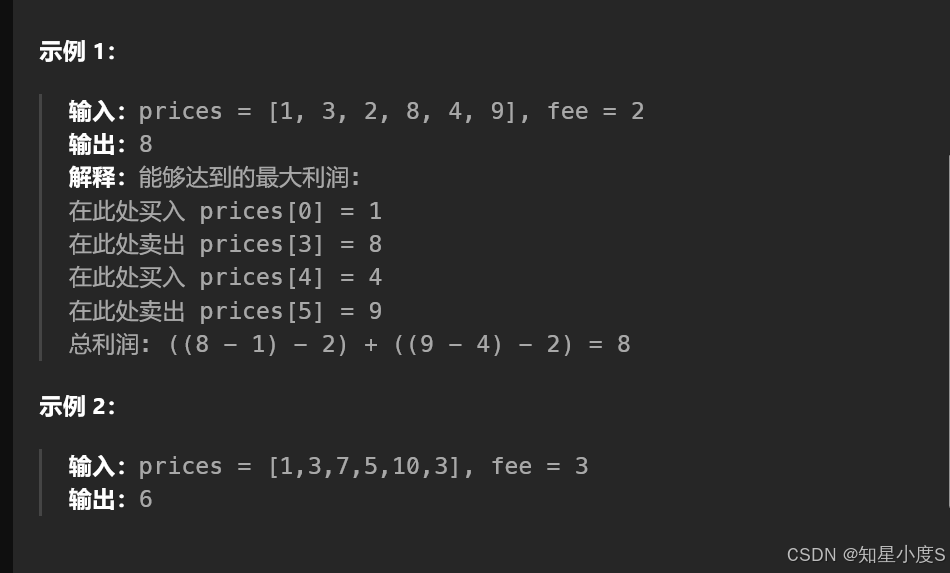
结合前面动态规划的经验，我们第一步就是进行状态表示：

1、状态表示

结合前面的经验和题目要求，我们可以这样进行状态表示：

dp表中的dp[i]表示为第i天结束后获得的最大利润~

事实上，dp【i】还可以继续细分，因为第【i】天结束后，可能处于买入状态（手里面有股票的状态），还有可能处于卖出状态（手里面没有股票的状态）

既然每一个位置都有两个状态，那么我们就需要创建两个dp表表示不同位置可能的状态~

两种方法： ①创建n*2的二维数组，dp【i】【j】，第一个下标表示在哪一天，第二个下标表示在当前天结束后的状态~（可以0表示买入状态，1表示卖出状态） ②直接创建两个dp表，一个dp表表示买入状态，一个dp表表示卖出状态

这里细分的状态比较少，我们就直接创建两个dp表

结合这里的题目要求+经验： dp1表中的dp1[i]表示为第【i】天结束后处于买入状态（手里面有股票）的最大利润~ dp2表中的dp2[i]表示为第【i】天结束后处于卖出状态（手里面没有股票）的最大利润~

接下来画图分析这两个状态之间的关系（也就是讨论状态相互之间是否可达以及是否可以自己到自己）

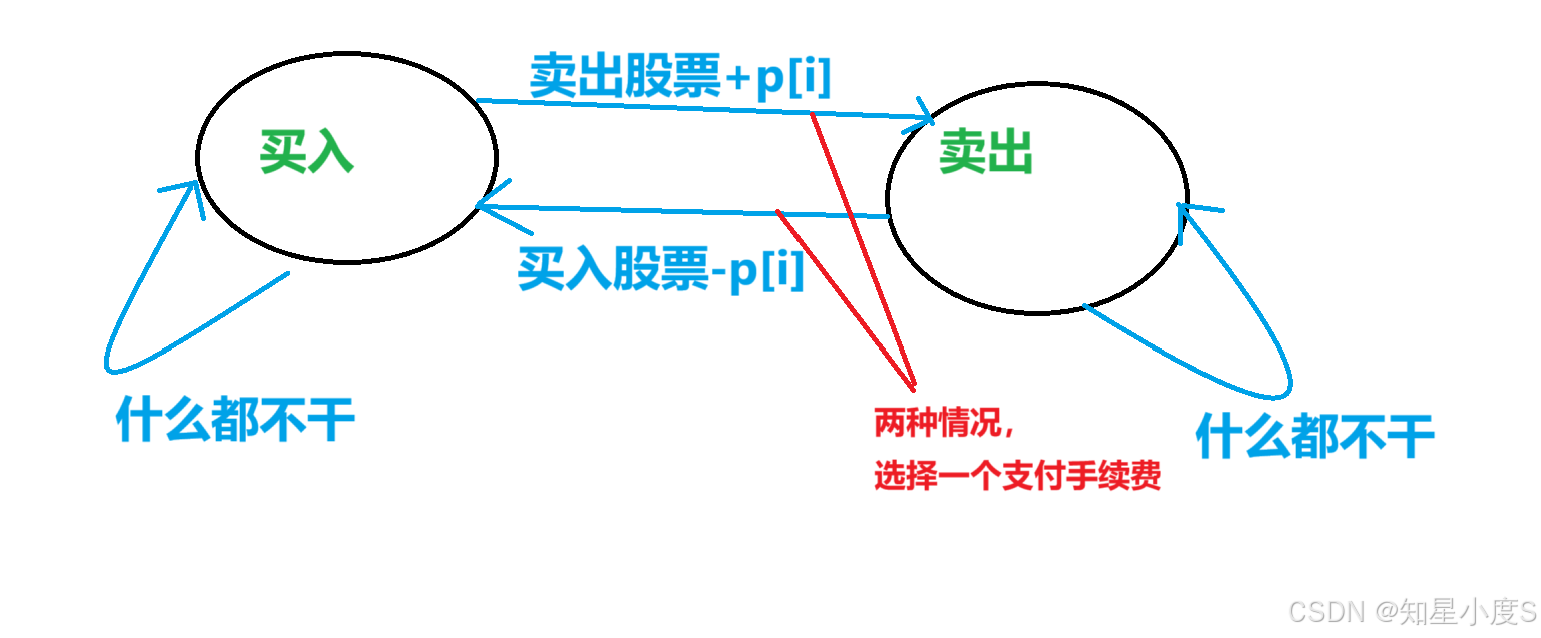
知道了这两个状态之间的关系，我们就可以继续利用动态规划的思想进行分析：

2、状态转移方程

我们以离【i】位置最近的状态分析状态转移方程，处理dp表 1、怎么样会处于买入状态呢？结合前面的画图分析可能是前一天卖出状态下，在今天买入股票变成买入状态；也可能是前一天买入状态下，今天什么都不干依然是买入状态，取两种情况的较大值~ dp1表状态转移方程： dp1[i]=max(dp1[i-1],dp2[i-1]-prices[i]); 2、怎么样会处于卖出状态呢？结合前面的画图分析可能是前一天买入状态，今天卖出股票就是卖出的状态；也可能是前一天卖出状态下，今天什么都不干依然是卖出状态，取两种情况的较大值~我们这里卖出了，一次交易完成就支付手续费~ dp2表状态转移方程： dp2[i]=max(dp2[i-1],dp1[i-1]+prices[i]-fee); 这个题目涉及到手续费，一次买入卖出需要交手续费，按理来说，我们可以任意选择一个dp表处理手续费就可以了，我们这里选择的是卖出了， 一次交易完成就支付手续费~

3、初始化

我们可以看到，状态转移方程里面有i-1,当i=0的时候显然会出现越界的情况，所以我们需要进行初始化结合前面如果不想初始化太麻烦，我们可以多申请一些空间，但是事实上这个题目初始化比较简单，直接初始化dp1[0],dp2[0]就可以了，所以我们直接进行初始化~ dp1[0]就是第一天操作后处于买入状态，那么利润为-prices[0]; dp2[0]就是第一天操作后处于卖出状态，那就是什么都不干，那么利润为0; 那么我们初始化结果就是 dp1[0]=-prices[0] , dp2[0]=0

4、填表顺序

我们这里的逻辑是从前面依次推出后面的，所以填表顺序是从前往后

5、返回结果

这里返回结果是到最后一天结束后的最大利润，最后一天结束后有两种状态，返回最大值就可以了，即返回return max(dp1[n-1],dp2[n-1]); 当然，最后一天是不可能还处于买入状态的，手里面还有股票就没有更多的赚钱啊，这样就不是最大利润，也就可以直接返回return dp2[n-1]；

选择自己喜欢的方式就好了

接下来，进行代码实现：

//买卖股票的最佳时机含手续费
class Solution
{
public:
    int maxProfit(vector<int>& prices, int fee)
    {
        int n = prices.size();
        //创建dp表
        vector<int> dp1(n);//买入（手里面有股票）
        vector<int> dp2(n);//卖出（手里面没有股票）

        //初始化
        dp1[0] = -prices[0];
        dp2[0] = 0;

        //填表
        for (int i = 1; i < n; i++)
        {
            dp1[i] = max(dp1[i - 1], dp2[i - 1] - prices[i]);
            dp2[i] = max(dp2[i - 1], dp1[i - 1] + prices[i] - fee);
        }

        //返回结果
       // return max(dp1[n-1],dp2[n-1]);
        return dp2[n - 1];
    }
};

如果是第一个dp表处理手续费呢？如果是买入进行手续费的扣除，那么初始化的时候【0】位置结束后处于买入状态，我们就需要扣除手续费fee，这样才不会出错~

代码实现：

class Solution
{
public:
    int maxProfit(vector<int>& prices, int fee)
    {
        int n = prices.size();
        //创建dp表
        vector<int> dp1(n);//买入（手里面有股票）
        vector<int> dp2(n);//卖出（手里面没有股票）

        //初始化
        dp1[0] = -prices[0] - fee;//买入就支付手续费
        dp2[0] = 0;

        //填表
        for (int i = 1; i < n; i++)
        {
            dp1[i] = max(dp1[i - 1], dp2[i - 1] - prices[i] - fee);
            dp2[i] = max(dp2[i - 1], dp1[i - 1] + prices[i]);
        }

        //返回结果
       //return max(dp1[n-1],dp2[n-1]);
        return dp2[n - 1];
    }
};

顺利通过~

买卖股票的最佳时机Ⅲ

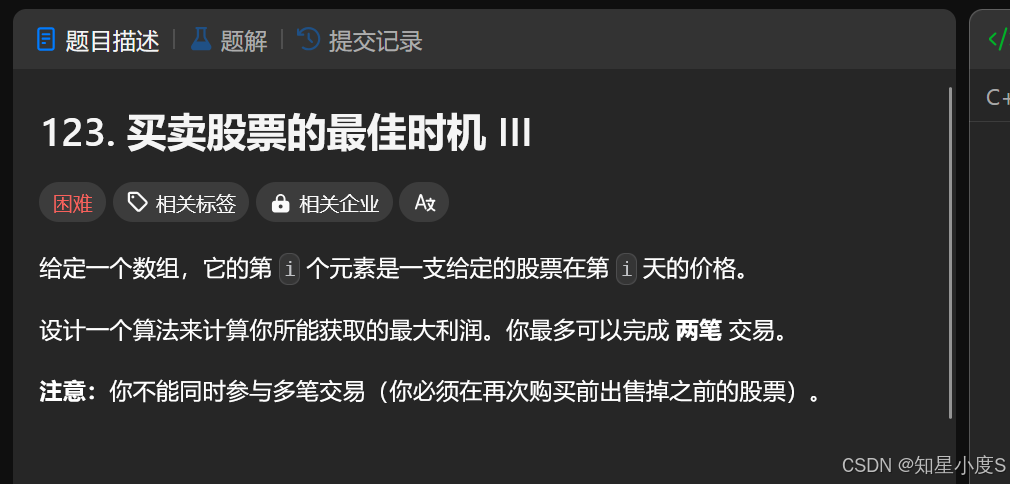
这个题目显然难度上升了，以前的股票问题并没有限制交易次数，但是这一个股票问题对我们的交易次数进行了限制，最多交易两次，那么也就说明可以交易0、1、2次，我们依然结合动态规划的思想来分析：

1、状态表示

结合前面的经验和题目要求，我们可以这样进行状态表示：

dp表中的dp[i]表示为第i天结束后获得的最大利润~

事实上，dp【i】还可以继续细分，因为第【i】天结束后，可能处于买入状态（手里面有股票的状态），还有可能处于卖出状态（手里面没有股票的状态）~我们可以直接创建两个dp表，此外，这一个题目我们还需要注意的是交易的次数，那么我们也就可以再增加一维空间来统计交易次数~

所以我们的状态表示

结合这里的题目要求+经验： dp1表中的dp1[i][j] 表示为第【i】天结束后，完成【j】次交易处于买入状态（手里面有股票）的最大利润~ dp2表中的dp2[i][j]表示为第【i】天结束后，完成【j】次交易处于卖出状态（手里面没有股票）的最大利润~

接下来画图分析这两个状态之间的关系（也就是讨论状态相互之间是否可达以及是否可以自己到自己）

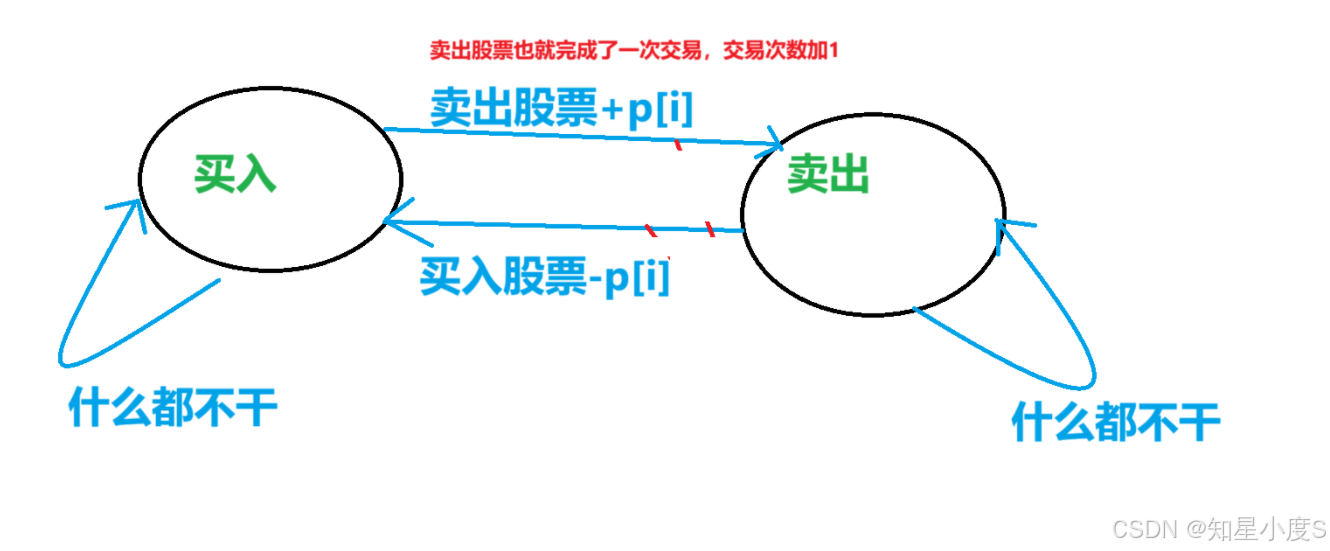
知道了这两个状态之间的关系，我们就可以继续利用动态规划的思想进行分析：

2、状态转移方程

我们以离【i】位置最近的状态分析状态转移方程，处理dp表 1、怎么样会处于买入状态呢？结合前面的画图分析可能是前一天卖出状态下，在今天买入股票变成买入状态；也可能是前一天买入状态下，今天什么都不干依然是买入状态，取两种情况的较大值~这两种情况都还没有卖出股票，没有完成一次交易，所以交易次数不变，也就是【j】不发生变化~ dp1表状态转移方程： dp1[i]=max(dp1[i-1][j],dp2[i-1][j]-prices[i]); 2、怎么样会处于卖出状态呢？结合前面的画图分析可能是前一天买入状态，今天卖出股票就是卖出的状态,有卖出股票完成了一次交易，所以交易次数应该加1，当前交易次数是【j】，那么原来交易次数为【j-1】，这样也就是交易次数+1；也可能是前一天卖出状态下，今天什么都不干依然是卖出状态，没有卖出股票，没有完成一次交易，所以交易次数不变。取两种情况的较大值~ dp2表状态转移方程： dp2[i]=max(dp2[i-1][j],dp1[i-1][j-1]+prices[i]);

3、初始化

我们可以看到，状态转移方程里面有i-1,j-1,当i=0,j=0的时候显然会出现越界的情况，所以我们需要进行初始化~ j-1很好处理，我们只需要判断j-1是否符合逻辑，不需要额外初始化~ 结合前面如果不想初始化太麻烦，我们可以多申请一些空间，但是事实上这个题目初始化比较简单，直接初始化第【0】天就可以了，所以我们直接进行初始化~第【0】天可能交易了0，1，2次，显然交易1，2次是没有意义的，因为没有利润，所以我们就需要把它们设置为一个比较小的值，如果直接使用INT_MIN可能会存在溢出的风险（因为计算过程有需要加减数据的情况），所以我们这里折半取-0x3f3f3f3f(保证比正常情况下计算结果小就可以了）

dp1[0][0]就是第一天完成0次交易后处于买入状态，说明买入了股票，那么利润为-prices[0]; dp2[0][0]就是第一天完成0次交易后处于卖出状态，那就是什么都不干，那么利润为0;

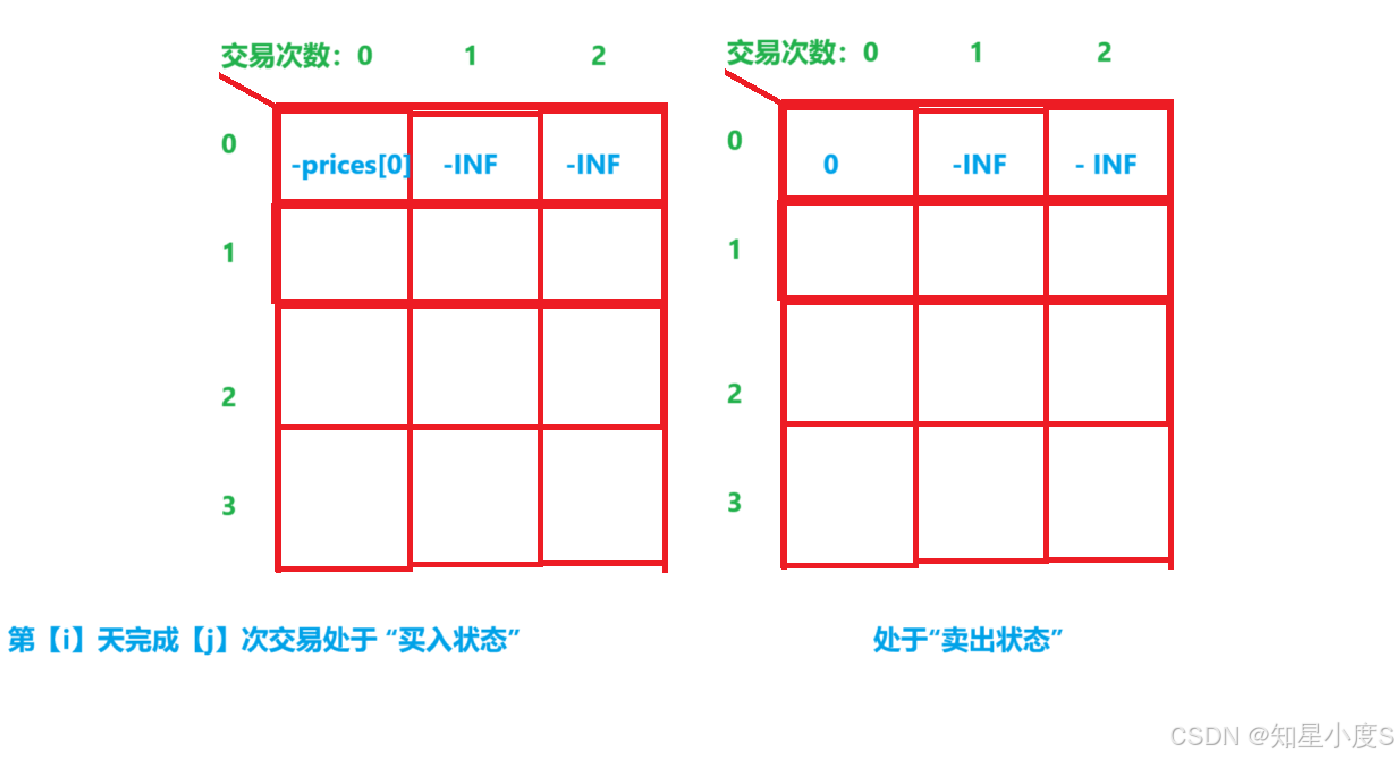
那么我们初始化结果就是 dp1[0][0]=-prices[0] , dp2[0][0]=0 ,其他初始化为-0x3f3f3f3f，也就是-INF

4、填表顺序

我们这里的逻辑是从上面推导到下面，每一行从前面依次推出后面的，所以填表顺序是从上向下，从前往后

5、返回结果

同理，最后一天是不可能还处于买入状态的，手里面还有股票肯定就没有赚更多的钱啊，这样就不是最大利润，但是最后一天处于卖出状态可能完成了0、1、2次交易，我们需要取它们的最大值进行返回，也就是返回return max(dp2[n-1][0],dp2[n-1][1],dp2[n-1][2]；

代码实现：

class Solution
{
    //取一个较小值
    const int INF = 0x3f3f3f3f;
public:
    int maxProfit(vector<int>& prices)
    {
        //1、创建dp表
        int n = prices.size();
        //可能完成0，1，2次交易
        vector<vector<int>> dp1(n, vector<int>(3, -INF));//买入
        auto dp2 = dp1;//卖出

        //2、初始化
        dp1[0][0] = -prices[0];
        dp2[0][0] = 0;

        //3、填表
        for (int i = 1; i < n; i++)
        {
            for (int j = 0; j < 3; j++)
            {
                //买入
                dp1[i][j] = max(dp1[i - 1][j], dp2[i - 1][j] - prices[i]);
                //卖出
                dp2[i][j] = dp2[i - 1][j];//dp2[i-1][j]一定存在
                //判断j-1是否符合逻辑
                if (j - 1 >= 0)
                {
                    //保证交易次数+1
                    dp2[i][j] = max(dp2[i - 1][j], dp1[i - 1][j - 1] + prices[i]);
                }
            }
        }

        //4、返回结果
        //最终卖出状态的最大值
        int ret = 0;
        for (int j = 0; j < 3; j++)
        {
            ret = max(ret, dp2[n - 1][j]);
        }

        return ret;
    }
};

顺利通过~

买卖股票的最佳时机Ⅳ

看见这个题目，就知道事情不简单，这不就是前面题目的最多进行2次变成了最多进行k次嘛，答案是的~所以我们只需要修改多增加一维空间的大小就可以了，逻辑是类似的，这里就不进行一步步分析了~

代码实现：

class Solution
{
    //取一个较小值
    const int INF = 0x3f3f3f3f;
public:
    int maxProfit(int k, vector<int>& prices)
    {
        int n = prices.size();
        //1、创建dp表
        // n*(k+1) ———— 交易0，1，2……k次
        vector<vector<int>> dp1(n, vector<int>(k + 1, -INF));//买入
        auto dp2 = dp1;//卖出

        //2、初始化
        dp1[0][0] = -prices[0];
        dp2[0][0] = 0;

        //3、填表
        for (int i = 1; i < n; i++)//i从1开始
        {
            for (int j = 0; j < k + 1; j++)
            {
                dp1[i][j] = max(dp1[i - 1][j], dp2[i - 1][j] - prices[i]);
                dp2[i][j] = dp2[i - 1][j];
                //减少初始化情况
                //j-1存在
                //if(j>=1 && (dp1[i][j-1]+prices[i]>dp2[i-1][j]))
                   // dp2[i][j]=dp1[i][j-1]+prices[i];
                if (j >= 1)
                    dp2[i][j] = max(dp2[i - 1][j], dp1[i][j - 1] + prices[i]);
            }
        }

        //4、返回结果
        int ret = 0;
        for (int j = 0; j < k + 1; j++)
        {
            ret = max(ret, dp2[n - 1][j]);
        }
        return ret;
    }
};

顺利通过~

事实上，这个题目还有一个小细节问题，就是如果k大于n，那么多出来的交易就是在某一天买入卖出，显然这是没有利润的，所以我们可以对k取min(k,n/2)来提高效率~

class Solution
{
    //取一个较小值
    const int INF = 0x3f3f3f3f;
public:
    int maxProfit(int k, vector<int>& prices)
    {
        int n = prices.size();
        //小细节优化
        k = min(k, n / 2);
        //1、创建dp表
        // n*(k+1) ———— 交易0，1，2……k次
        vector<vector<int>> dp1(n, vector<int>(k + 1, -INF));//买入
        auto dp2 = dp1;//卖出

        //2、初始化
        dp1[0][0] = -prices[0];
        dp2[0][0] = 0;

        //3、填表
        for (int i = 1; i < n; i++)//i从1开始
        {
            for (int j = 0; j < k + 1; j++)
            {
                dp1[i][j] = max(dp1[i - 1][j], dp2[i - 1][j] - prices[i]);
                dp2[i][j] = dp2[i - 1][j];
                //减少初始化情况
                //j-1存在
                //if(j>=1 && (dp1[i][j-1]+prices[i]>dp2[i-1][j]))
                   // dp2[i][j]=dp1[i][j-1]+prices[i];
                if (j >= 1)
                    dp2[i][j] = max(dp2[i - 1][j], dp1[i][j - 1] + prices[i]);
            }
        }

        //4、返回结果
        int ret = 0;
        for (int j = 0; j < k + 1; j++)
        {
            ret = max(ret, dp2[n - 1][j]);
        }
        return ret;
    }
};