算法训练之分治（快速排序）

什么是分治算法？

听分治算法这个名字，事实上，我们可以知道分治就是分而治之~

分治算法通过【"分解——解决——合并"】三步解决复杂问题： 1）递归将问题拆分为独立子问题（如归并排序拆分数组）； 2）基线条件直接求解小规模问题； 3）合并子问题结果（如合并有序子数组）。 典型应用包括快速排序（O(n log n)）、大数乘法（Karatsuba算法）及二分查找。其优势在于降低算法复杂度、支持并行计算，但递归调用可能增加空间开销。与动态规划不同，分治适用于子问题独立的场景，而动态规划通过记忆化解决重叠子问题。

只是说概念，可能很难理解，接下来，我们在题目中使用分治的思想来解决问题~

颜色分类

在正式开始运用分治算法之前，我们首先来看看颜色分类的问题，方便我们后面的学习~

颜色分类

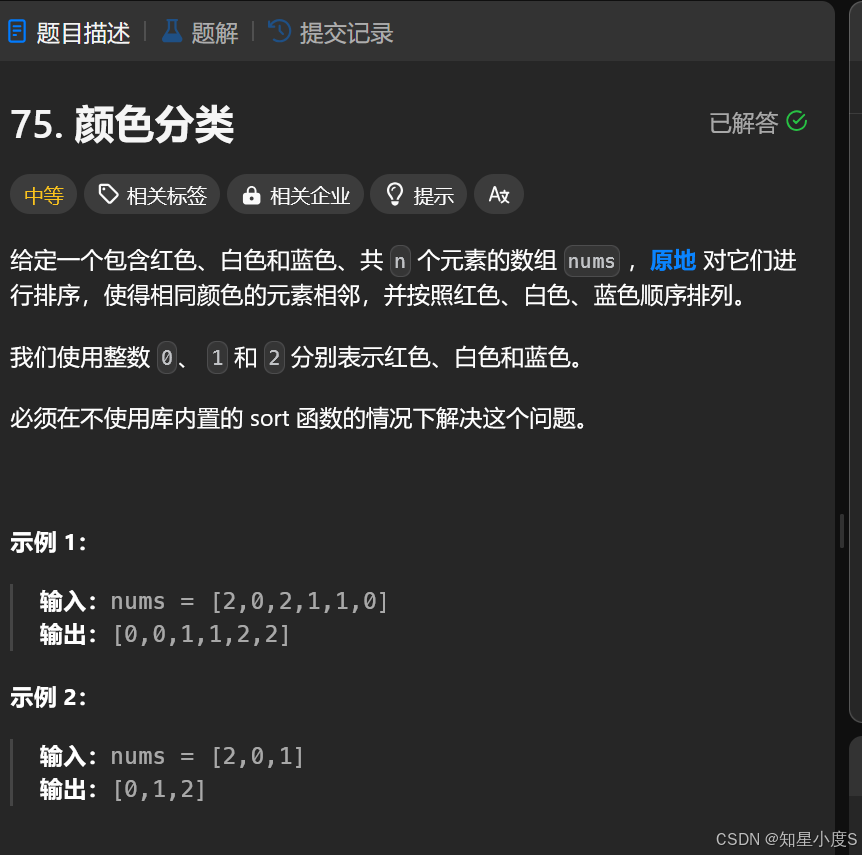
题目要求我们把按照红色，白色，蓝色的顺序把它们排序在一起，也就是0，1，2的顺序~并且是原地实现，同时不可以使用sort~

有人会说这个怎么办？别急！小编带着方法走来了~

解法：三指针

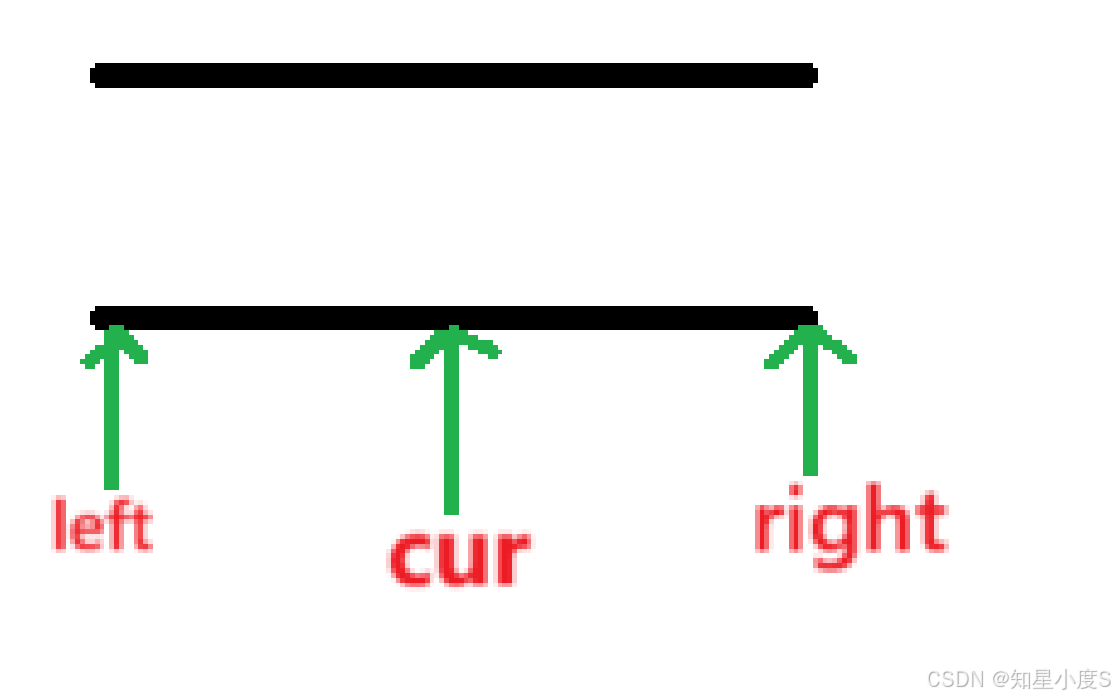
我们首先定义三个指针【left】，【cur】，【right】，然后通过这三个指针来进行区域划分，题目中是【0】【1】【2】这三个区域~我们根据题目要求进行区域表示~ left表示【0】区域的右边界 cur表示【1】区域的右边界后面的一个位置 right表示【2】区域的左边界 【cur】到【right-1】就是没有处理的区域 画图理解：

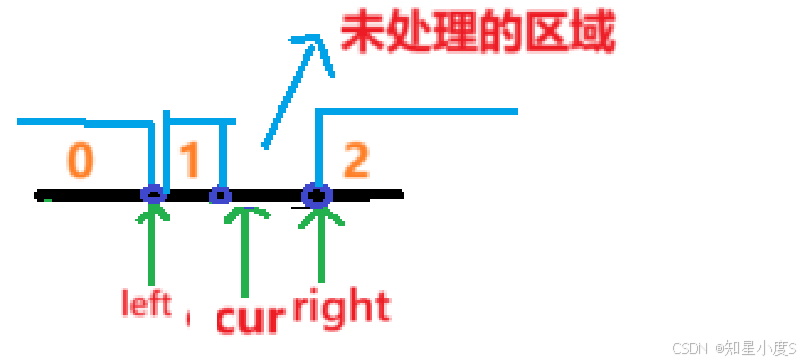
接下来就是怎么遍历才能得到区域划分的效果： cur进行遍历，有下面的三种情况： 如果nums【cur】为1，那么我们就可以交换nums【++left】和nums【cur】，根据我们的区域划分，++left原来的的内容是为0，cur直接进行++； 如果nums【cur】为1，直接cur++就可以了； 如果nums【cur】为2，那么我们就可以交换nums【--right】和nums【cur】，根据我们的区域划分，--right原来的的内容是我们还没有进行处理的元素，所以cur就不需要进行++； 这样子的区域划分，我们就得到了 【0，left】就是【0】区域 【left，cur-1】就是【1】区域 【right，n-1】就是【2】区域 当cur与right相遇的时候，我们的所有元素就处理结束了~

有了前面的分析，这里的代码实现就比较简单了~

代码实现：

//颜色分类
class Solution
{
public:
    void sortColors(vector<int>& nums)
    {
        int n = nums.size();
        //三指针
        int left = -1, cur = 0, right = n;
        //cur进行遍历
        while (cur < right)//cur与right相遇就处理完了
        {
            //分情况讨论
            if (nums[cur] == 0)
            {
                swap(nums[++left], nums[cur++]);
                //left前置++,先到后面的一个位置再进行交换
            }
            else if (nums[cur] == 2)
            {
                swap(nums[--right], nums[cur]);
                //right前置++,先到前面的一个位置再进行交换
                //前面的一个位置原来是没有被处理的元素，cur不需要++
            }
            else if (nums[cur] == 1)
            {
                cur++;//cur直接++
            }
        }
        for (auto e : nums)
        {
            cout << e << " ";
        }
    }
};

顺利通过~

这个解法时间复杂度为O（N），空间复杂度为O（1），还是十分优秀的~

排序数组

排序数组

有了前面的基础，接下来我们来看看排序数组这样一道题目~

我们的算法思想是使用分治（快速排序），在数据结构的博客中我们就提到过快速排序算法，可以参考这篇博客：数据结构——排序（续集）

其中最重要的一步就是找基准值，以前的算法时间复杂度：我们知道递归的时间复杂度=递归的次数*一次递归的时间复杂度，因为不断地进行二分，我们认为递归的次数为logN，那么时间复杂度为O（N*logN），但是如果数组所有元素相等或者已经有序，那么递归的次数为N，时间复杂度为O（N*N），以前的找基准值的方法就不太适用了~

这里我们就采用前面颜色分类题目中使用到的数组分块的方法~

解法： 将数组动态划分为三个连续区间：左侧区间存储所有小于基准值的元素，中间区间存储所有等于基准值的元素，右侧区间存储所有大于基准值的元素。后续递归过程仅需对左右两个非稳定区间继续执行划分操作（中间已稳定的相等区间可直接跳过），同时我们采用随机基准选择的方法，来避免避免最坏时间复杂度 O(n²)~ 例：

• 固定选择策略：输入[1,2,3,4,5]会导致每次基准选到最小值，产生n次线性扫描
• 随机选择策略：同一输入有极大概率在首轮选择中间值（如3），将数组划分为[1,2]和[4,5]，后续递归深度降至log n级别

这种优化策略在处理包含大量重复元素的数据集时，能够显著减少无效比较次数，从而大幅提升算法效率。

解法具体实现流程如下： a. 定义递归出口 当待处理的子数组长度小于等于1时，直接结束当前递归（单个元素无需排序）。 b. 随机选择基准元素

1. 在程序初始化时设置随机数生成器（可以通过时间戳播种）
2. 生成一个位于当前处理区间内的随机下标（通过取模运算确保随机性）
3. 以该下标对应的元素作为本次划分的基准值

c. 数组分块 通过三个动态边界指针将数组划分为三个连续区域：

• 左侧区域：所有元素均小于基准值（通过从左向右扫描，将较小元素交换至此）
• 中间区域：所有元素均等于基准值（天然有序，无需后续处理）
• 右侧区域：所有元素均大于基准值（通过从右向左扫描，将较大元素交换至此）

最终形成三个逻辑区间： [ 小于基准值的元素 ] [ 等于基准值的元素 ] [ 大于基准值的元素 ] d. 递归处理左右区域 仅对左侧和右侧两个非稳定区间继续执行快速排序流程，跳过中间已稳定的相等值区域。 算法优势： 这种三向切分策略在处理包含大量重复元素的数据集时具有显著优势。传统快速排序需要对所有元素进行两两比较，而优化后算法通过预先分离相等值区域，可减少比较次数，在极端重复数据场景下时间复杂度趋近于O(n)~

【随机基准选择模块】 函数定义：int GetRandomKey(vector& nums, int left, int right) 实现步骤： a. 在程序入口处初始化随机数生成器（如srand(time(0))） b. 在基准选择函数内部生成随机数（如rand()） c. 通过取模运算将随机数映射到有效区间：[left, right] 具体转换公式：随机下标 = left + (rand() % (right - left + 1))

代码实现：

class Solution
{
public:
    vector<int> sortArray(vector<int>& nums)
    {
        //时间戳种下种子
        srand(time(NULL));
        int n = nums.size();
        qsort(nums, 0, n - 1);//调用快速排序
        return nums;
    }
    int GetRandomKey(vector<int>& nums, int left, int right)
    {
        int ran = rand();//生成随机数
        //随机数对当前长度取模+left
        //得到当前区间随机下标——根据下标确定随机值
        return nums[ran % (right - left + 1) + left];
    }
    void qsort(vector<int>& nums, int l, int r)
    {
        //递归结束条件
        if (l >= r)
            return;
        //随机获取当前区间里面的基准值
        int key = GetRandomKey(nums, l, r);
        //遍历数组进行数组分块
        int left = l - 1, cur = l, right = r + 1;
        while (cur < right)
        {
            //根据key分情况讨论
            if (nums[cur] < key)
            {
                swap(nums[++left], nums[cur++]);
            }
            else if (nums[cur] == key)
            {
                cur++;
            }
            else if (nums[cur] > key)
            {
                swap(nums[--right], nums[cur]);
            }
        }
        //[left+1,cur]是元素相等的区间，不需要处理
        //递归处理剩下的区间
        qsort(nums, l, left);
        qsort(nums, right, r);
        //qsort(nums,cur,r);//也可以，最终cur==right
    }
};

顺利通过~

这个解法就使用了随机选择基准值+数组分块的算法十分巧妙~对我们的效率有了很大的提高