【机器学习 | XGBOOST原理&实现】
原创【机器学习 | XGBOOST原理&实现】
原创
九年义务漏网鲨鱼
发布于 2025-07-22 15:17:05
发布于 2025-07-22 15:17:05
一、基本内容
- 基本内容:GBDT的基础上,在损失函数上加入树模型复杂度的正则项
与GBDT一样,也是使用新的弱学习器拟合残差(当前模型负梯度,<u>残差方向</u>)
- GBDT损失函数
- XGboost损失函数
- 正则项
其中,L 表示当前弱学习器的叶子节点个数,\gamma,\lambda 表示惩罚项,\omega_j 表示当前弱学习器的叶子节点$j$值。
二、目标函数优化
弱学习器损失函数可以写为:
其中,y_i^t = y_i^{t-1}+\omega_j ,表示当前的预测输出概率为前t-1 个学习器的输出结果加上当前学习器的输出,y_i^{t-1} 为常数;
目标函数:
泰勒二阶展开基础公式:f(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{1}{2}f''(x_0)(x-x_0)^2
在目标优化中,对函数L(y_i, y_i^{t-1}+\omega_j) 二阶泰勒展开,可得:
舍去常数项,令$g_i=L'(y_i, y_i^{t-1})\omega_j,h_i =\frac{1}{2}L''(y_i, y_i^{t-1})\omega_j^2 $,表示第$i$个样本的真实值与前$t-1$弱学习器模型输出值的损失导数
令$Gi=\sum{i=1}^{N}gi,H_i= \sum{i=1}^{N}h_i$,最后的优化目标函数可以写为:
可以发现,目标函数是关于$\omega$的二次函数,使得损失最小的$\omega$值为:
\omega 代入目标函数,可得:
三、树结构的确定
3.1 穷举法
逐一举例,时间复杂度过大,不可能实现
3.2 精确贪心算法
基本原理与决策树的结点选取类似,以
信息增益的思想,遍历所有特征以及阈值选取当前节点的特征和阈值
假设当前叶子结点数为$1$,进一步划分的叶子节点数目为2,假设划分后的左子结点的样本二阶导之和为$G_L$,同理右子节点的样本二阶导之和为$G_R$,则未划分前应该是二者之和.损失减少,则表明当前分裂work,记录当前分裂特征和阈值,$Gain$越大,表明效果越好
3.3 列采样
一种对特征降采样的方式:选取一定的特征分裂,每一个弱学习器选取子特征集,例如从原有特征选择80%的特征,而弱学习器的每一个结点也可以在当前树下的子特征集重新随机选取,也可以全部使用进行遍历。
3.4 特征值分桶法
一种对==特征值降采样==的方式:对特征的值进行分桶,例如某一特征的值为0-9,分为五个桶只需要遍历五次,大大增加运算效率,桶数越大,与精确贪心算法的越接近,当每个桶只有一个样本时,即为精确贪心算法。
- 全局策略:分裂结点的特征一样时,当前弱学习器的分桶阈值不变;
- 局部策略:分裂结点的特征一样,当前弱学习器的新结点也会重新计算分桶阈值;
在论文中,桶的数目个数计算为:
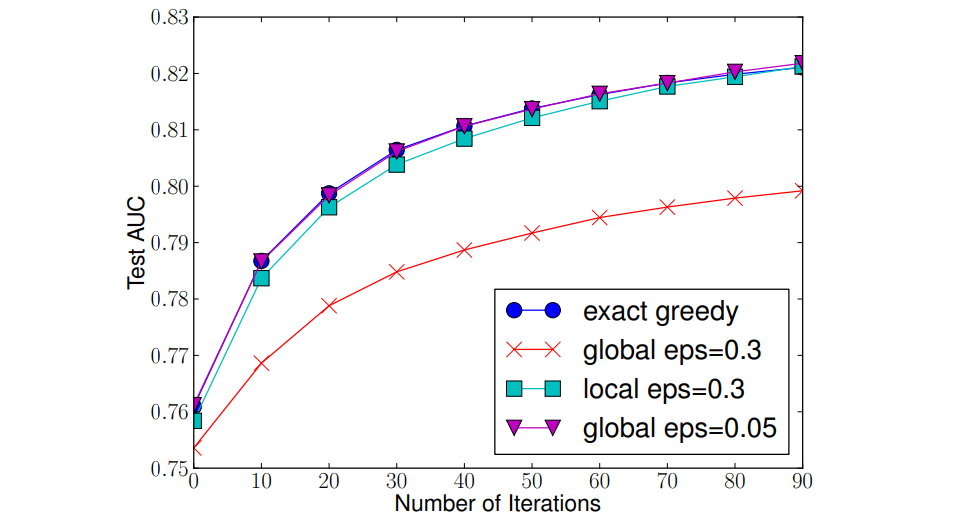
如图可以得到以下结论:
- 局部策略在一般情况下比全局策略好;
- 当$eps$足够小时,时间复杂度以及精度是与精确贪心算法接近的,并且效果优于局部策略;
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
评论
登录后参与评论
推荐阅读
目录

