时间序列复杂度

Zeusro

修改于 2025-09-08 10:40:36

660

文章被收录于专栏：ZeusroZeusro

传统时间空间复杂度

时间复杂度（Time Complexity）描述的是：算法执行所需的时间与输入规模之间的关系。

一般来说，O(1) < O(\log n) < O(n) < O(n\log n) < O(n^2) < O(2^n) < O(n!)

空间复杂度（Space Complexity）描述的是：算法执行过程中所需内存空间与输入规模之间的关系。

它主要反映了算法对内存资源的消耗。

常见空间复杂度：

O(1)：只使用常数个额外变量，例如交换两个数。
O(n)：需要开辟与输入规模等长的数组，比如 BFS 队列。
O(n^2)：存储二维矩阵。
O(n \log n)：归并排序时的辅助数组。
O(n!)：存储所有排列结果。

时间序列复杂度

时间序列复杂度（Time Series Complexity）描述的是：在满足时间复杂度以及空间复杂度的前置性论述下，算法执行的实际时间以及内存资源的利用效率。

时间序列复杂度是一个二维图表。X轴是t，Y轴是(used - buff/cache) / total

时间序列复杂度需要对程序进行可观测性分析。个人比较喜欢指数衰减型。

//oracle:画一个二维坐标系，横轴是t，Y轴是(used - buff/cache) / total ，只需要第一象限，包含指数增长模拟摩尔定律的例子，以及相对称指数衰减图表。

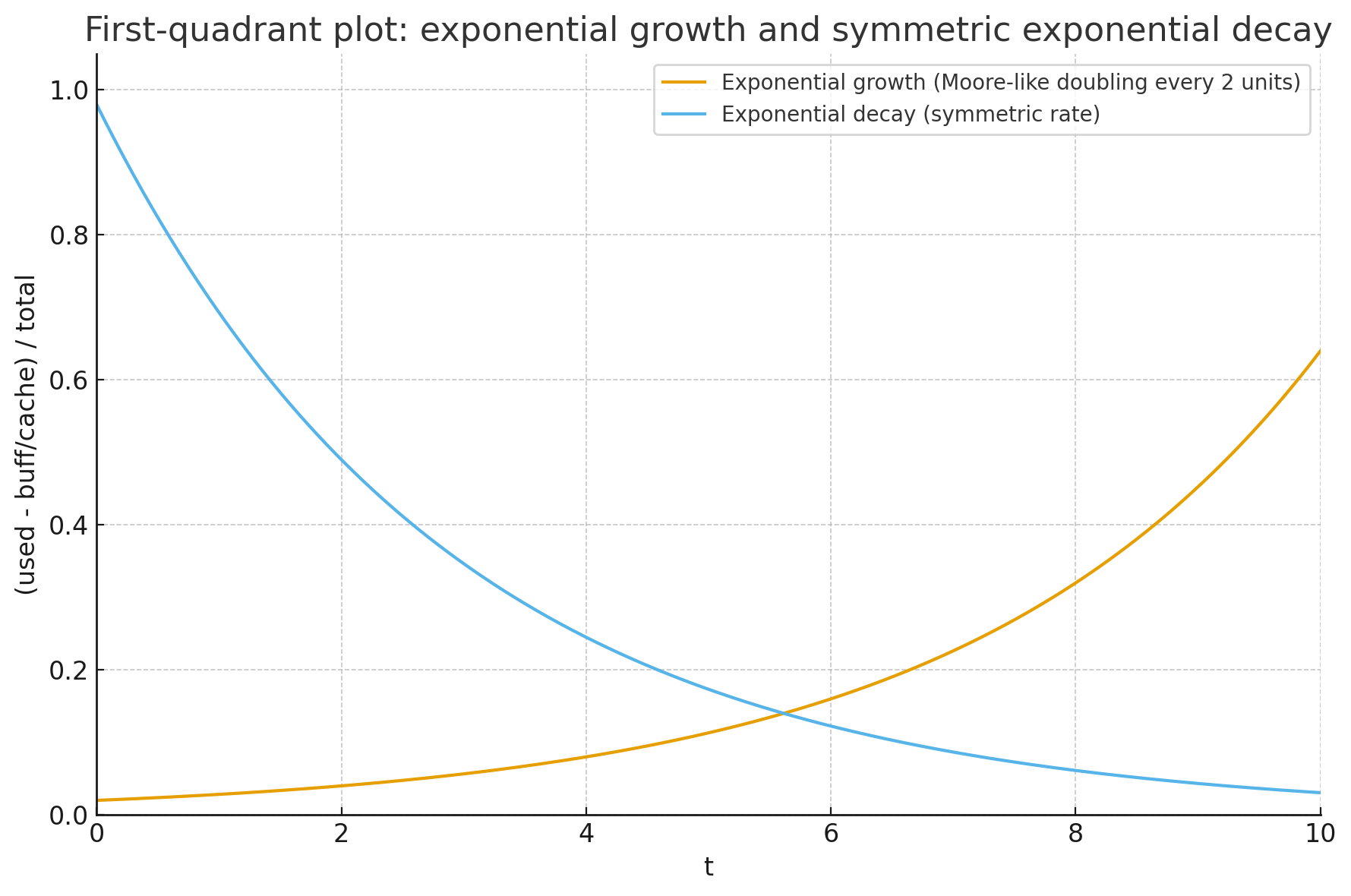
具体例子

时间序列复杂度的这一概念，破除了传统时间空间算法复杂度的浅层优劣问题。说点人话，你可以用一个看起来很傻的程序去模拟AI，只要这个“AI”能骗到人（通过图灵测试）。

伪AI电话

package main

import (
	"fmt"
	"time"
)

// 固定的话术脚本
var script = []string{
	"您好，这里是XX银行智能客服中心。",
	"我们最近推出了一款超低利率的信用贷款产品，年利率低至3.5%。",
	"无需抵押，最快30分钟即可放款，非常适合资金周转。",
	"请问您现在是否需要了解一下具体的办理流程呢？",
	"我们可以根据您的个人情况，提供最高50万的额度支持。",
	"办理过程全程在线，非常简单方便。",
	"如果您有兴趣，我可以帮您安排专属客户经理与您联系。",
	"感谢您的来电，希望我们的贷款产品能帮到您！",
}

func fakeLoanCall() {
	fmt.Println("📞 电话拨号中...")
	time.Sleep(time.Second * 2)
	fmt.Println("AI：嘟嘟嘟……接通成功！")

	for _, line := range script {
		time.Sleep(time.Second * 2)
		fmt.Println("AI：", line)

		// 模拟用户反应
		time.Sleep(time.Second)
		fmt.Println("你：嗯……好的。")
	}
	fmt.Println("📞 通话结束，感谢使用伪AI电话营销系统。")
}

func main() {
	fakeLoanCall()
}

📞 电话拨号中...
AI：嘟嘟嘟……接通成功！
AI： 您好，这里是XX银行智能客服中心。
你： 嗯……好的。
AI： 我们最近推出了一款超低利率的信用贷款产品，年利率低至3.5%。
你： 嗯……好的。
AI： 无需抵押，最快30分钟即可放款，非常适合资金周转。
你： 嗯……好的。
AI： 请问您现在是否需要了解一下具体的办理流程呢？
你： 嗯……好的。
AI： 我们可以根据您的个人情况，提供最高50万的额度支持。
你： 嗯……好的。
AI： 办理过程全程在线，非常简单方便。
你： 嗯……好的。
AI： 如果您有兴趣，我可以帮您安排专属客户经理与您联系。
你： 嗯……好的。
AI： 感谢您的来电，希望我们的贷款产品能帮到您！
你： 嗯……好的。
📞 通话结束，感谢使用伪AI电话营销系统。

或者换一种思路，你可以用一台十年前的安卓机去证明自己，也可以找你爸要一个亿,买一台带超强GPU的至强服务器，去算1+1=2。这就是一种个人选择，无关乎对错问题。