《掰开揉碎讲编程-长篇》一文读懂 哈希表
原创《掰开揉碎讲编程-长篇》一文读懂 哈希表
原创
博主粉丝群介绍: ① 群内初中生、高中生、本科生、研究生、博士生遍布,可互相学习,交流困惑。
② 热榜top10的常客也在群里,也有数不清的万粉大佬,可以交流写作技巧,上榜经验,涨粉秘籍。
③ 群内也有职场精英,大厂大佬,可交流技术、面试、找工作的经验。
进群免费赠送写作秘籍一份,助你由写作小白晋升为创作大佬。
进群赠送CSDN评论防封脚本,送真活跃粉丝,助你提升文章热度。
群公告里还有全网大赛and约稿汇总/博客提效工具集/CSDN自动化运营脚本 有兴趣的加文末联系方式,备注自己的CSDN昵称,拉你进群,互相学习共同进步。- 刷算法题的时候,别人的题解总是:"加个哈希表,O(n)秒了"。而你还在纠结:哈希表是什么?为什么能加速?怎么用? 这篇文章就是来解答这些问题的。
前置知识要求
知识点 | 重要程度 | 说明 |
|---|---|---|
数组基础 | 必需⭐ | 需要了解数组的基本操作和时间复杂度 |
时间复杂度 | 必需⭐ | 需要理解 O(1)、O(n) 等概念 |
基础编程语法 | 推荐 | 会使用一门编程语言即可 |
链表 | 加分项 | 了解更佳,不了解也不影响 |
- 必需:没有这个基础很难理解本文
- 推荐:有这个基础学习更轻松
- 加分项:了解更好,不了解也不影响
为什么叫Hash?
Hash 的英文原意就是"切碎、混杂"。想象你在炖一锅大杂烩(hash):胡萝卜、土豆、红肉、白肉……很多复杂叫不出名的食材混合在一起煮,最后成了一锅汤。
这个过程就是哈希。
原本各有特点的食材(数据),经过烹煮(哈希函数),变成了一锅融合的汤(Hash值)。
哈希的本质:把不能当索引的东西(字符串、对象)变成能当索引的数字,但对外呈现为键值对,更符合人类思维。
和数组有什么关系?
数组是怎么组织数据的?
通过序号(索引),像门牌号一样:
数组:[苹果, 芒果, 葡萄, 草莓, 西瓜]
索引: 0 1 2 3 4问题来了:我想找到"葡萄"要怎么找?
方法1:暴力查找(遍历挨个比对)
第1步:看索引0 → "苹果" 不是
第2步:看索引1 → "芒果" 不是
第3步:看索引2 → "葡萄" 找到了!时间复杂度:O(n) —— 最坏情况要找 n 次
但如果我知道索引呢?
直接访问:数组[2] → "葡萄" 一次搞定!时间复杂度:O(1) —— 直达,不用挨个找
矛盾点
- 问题:我现在有"葡萄"这个名字,但不知道它在索引几
- 理想状态:能不能通过"葡萄"这个名字,直接算出它在索引 2?
哈希表就是来解决这个问题的!
哈希表的做法
用哈希函数把"葡萄"变成索引
第一步:设计一个哈希函数(就像炖汤的配方)
hash("葡萄") = 2 ← 把"葡萄"这个字符串"煮"成数字2
第二步:存储时
"葡萄" → hash("葡萄") = 2 → 存到数组[2]的位置
第三步:查找时
想找"葡萄"?
→ hash("葡萄") = 2
→ 直接去数组[2]拿
→ 时间复杂度:O(1)!对比总结
查找方式 | 普通数组遍历 | 哈希表 |
|---|---|---|
操作 | 从头到尾挨个比对 | 通过哈希函数直接定位 |
过程 | 苹果 → 芒果 → 葡萄 | hash("葡萄")=2 → 数组2 |
时间复杂度 | O(n) | O(1) |
特性 | 普通数组 | 哈希表(基于数组) |
|---|---|---|
底层结构 | 数组 | 数组 |
索引是什么 | 必须是连续的数字 0,1,2,3... | 任意类型(通过哈希函数转成数字) |
存储方式 |
|
|
查找速度 | O(1)(知道索引)不知道O(n) | O(1) 平均 / O(n) 最坏 |
哈希表在代码中长什么样?(Java)
在 Java 中,哈希表的表现形式为键值对(Key-Value)
// Java 中的 HashMap
HashMap<String, String> fruitMap = new HashMap<>();
// 存储:键 → 值
fruitMap.put("apple", "苹果");
fruitMap.put("grape", "葡萄");
fruitMap.put("mango", "芒果");
// 查找:通过键直接拿到值
String result = fruitMap.get("grape"); // 返回 "葡萄"键值对是什么?
就像字典一样:
英文(Key 键) 中文(Value 值)
─────────────────────────────
apple → 苹果
grape → 葡萄
mango → 芒果- Key(键):用来查找的"钥匙",比如 "apple"
- Value(值):存储的实际数据,比如 "苹果"
底层怎么存的?
还是用数组!
用户看到的(键值对形式):
"apple" → "苹果"
"grape" → "葡萄"
底层实际存储(数组):
[ null, null, "葡萄", "苹果", null ]
0 1 2 3 4
↑ ↑
hash("grape") hash("apple")
= 2 = 3过程:
- 你存入
"apple" → "苹果" - 哈希函数计算:
hash("apple") = 3 - 把 "苹果" 存到数组的
[3]位置 - 查找时:
hash("apple") = 3,直接去[3]拿
- 因为封装,我们可以不关注具体实现,实现也不是本文的重点,我们已经明白了哈希,接下来将讲在算法中如何使用哈希
哈希表中常用的方法有哪几个?
方法 | 描述 | 示例代码 |
|---|---|---|
| 向 |
|
| 根据给定的键返回对应的值,如果键不存在,则返回 |
|
| 检查 |
|
| 检查 |
|
| 删除指定键的键值对,返回该键的值,如果键不存在则返回 |
|
| 清空 |
|
| 返回 |
|
| 判断 |
|
| 返回 |
|
| 返回 |
|
| 返回 |
|
getOrDefault | 根据键 | map.getOrDefault("key1", "defaultValue"); |
实战:刷LeetCode时怎么用哈希表得到更好的时间复杂度?
简单题:难度1
给你一个整数数组 nums 。
如果一组数字 (i,j) 满足 nums[i] == nums[j] 且 i < j ,就可以认为这是一组 好数对 。
返回好数对的数目。
示例 1:
输入:nums = [1,2,3,1,1,3]
输出:4
解释:有 4 组好数对,分别是 (0,3), (0,4), (3,4), (2,5) ,下标从 0 开始
示例 2:
输入:nums = [1,1,1,1]
输出:6
解释:数组中的每组数字都是好数对
示例 3:
输入:nums = [1,2,3]
输出:0
提示:
1 <= nums.length <= 100
1 <= nums[i] <= 100
``` java- 算法小白,第一眼看过去肯定是用双重循环暴力破解,但咱们已经学过哈希了,应该能想到这道题要用哈希来做。
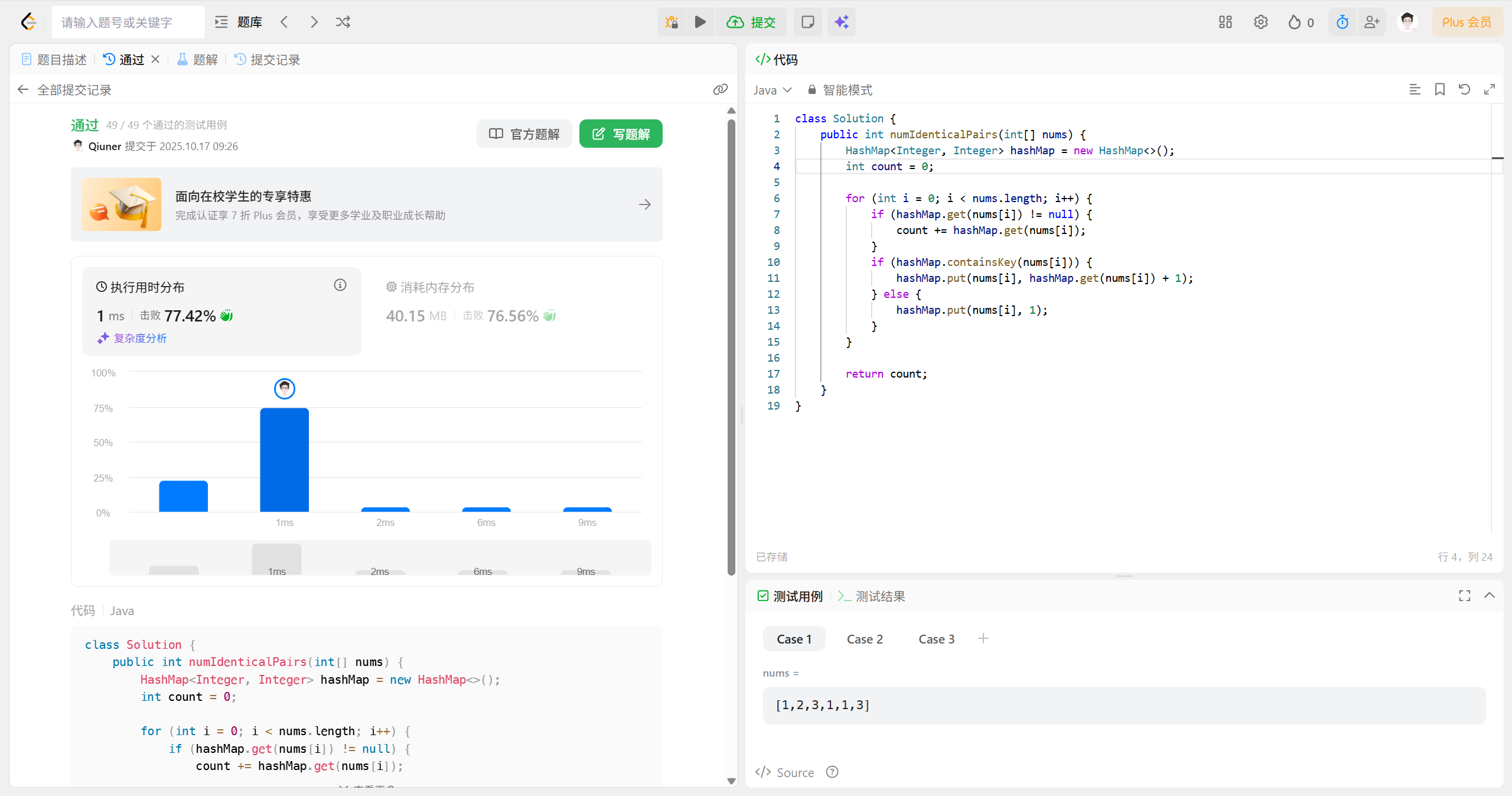
答案

class Solution {
// 定义方法,输入为整数数组,返回满足条件的配对数量
public int numIdenticalPairs(int[] nums) {
// 创建一个 HashMap 来存储每个数字出现的次数
HashMap<Integer, Integer> hashMap = new HashMap<>();
int count = 0; // 用来记录符合条件的配对数
// 遍历数组中的每个元素
for (int i = 0; i < nums.length; i++) {
// 如果该数字已经出现在哈希表中,累加已有的配对数
if (hashMap.get(nums[i]) != null) {
count += hashMap.get(nums[i]);
}
// 更新该数字在哈希表中的出现次数
if (hashMap.containsKey(nums[i])) {
hashMap.put(nums[i], hashMap.get(nums[i]) + 1);
} else {
hashMap.put(nums[i], 1);
}
}
return count; // 返回符合条件的配对数
}
}
通用小技巧
不知道你有没有一个感觉,觉得我文中的代码是可以化简的?
如果你没有这种感觉,那我建议回过头去看 哈希表中常用的方法有哪几个? 这一小结内容
if (hashMap.containsKey(nums[i])) {
hashMap.put(nums[i], hashMap.get(nums[i]) + 1);
} else {
hashMap.put(nums[i], 1);
}分割线
分割线,你可以自己想想
- 是的,可以变成这种一行的形式
hashMap.put(nums[i], hashMap.getOrDefault(nums[i], 0) + 1);简单题:难度2
给定两个字符串 s 和 t ,它们只包含小写字母。
字符串 t 由字符串 s 随机重排,然后在随机位置添加一个字母。
请找出在 t 中被添加的字母。- 也很简单,先把s出现过的字母全部put到哈希表里面去,然后再来个循环
答案

import java.util.HashMap;
class Solution {
public char findTheDifference(String s, String t) {
HashMap<Character,Integer> hash = new HashMap();
for(int i=0;i<s.length();i++){
char ch = s.charAt(i);
if (hash.containsKey(ch)) {
hash.put(ch, hash.get(ch) + 1);
} else {
hash.put(ch, 1);
}
}
for(int i=0;i<t.length();i++){
char ch =t.charAt(i);
if(hash.containsKey(ch)){
hash.put(ch,hash.get(ch)-1);
if(hash.get(ch)<0){
return ch;
}
}else{
return ch;
}
}
return ' ';
}
}如果你看到这段代码没有感觉到不对,那你一定没有仔细想过通用小技巧。
不难发现
if (hash.containsKey(ch)) {
hash.put(ch, hash.get(ch) + 1);
} else {
hash.put(ch, 1);
}这部分代码可以变成
hash.put(ch, hash.getOrDefault(ch, 0) + 1);中等题:难度4
- 这道题需要会回溯算法,哈希只起到一个存储字母映射的功能。不合适做教学
- 那就这样结束了
为什么会有不同的哈希表?
想象一下,你有100个格子,但要存1000个东西。哈希函数把不同的key算出了相同的位置,这就是"哈希冲突"。怎么办?
不同的哈希表就是用不同的方法来解决这个问题的。
主要的哈希表种类
链表法哈希表(最常见)
- 怎么做? 每个格子里放一个链表,冲突了就往链表后面加
- 优点: 简单粗暴,永远不会"满"
- 缺点: 链表太长查找就慢了
- 谁在用? Java的HashMap、Python的dict
开放寻址法哈希表
- 怎么做? 冲突了就继续往后找空位
- 优点: 数据紧凑,缓存友好,速度快
- 缺点: 容易"扎堆",删除操作麻烦
- 谁在用? Python早期版本、Redis的字典
布谷鸟哈希(Cuckoo Hashing)
- 怎么做? 用两个哈希函数,冲突了就把原来的元素"踢走"
- 优点: 查找超快,最坏情况也是O(1)
- 缺点: 插入可能触发连锁反应
- 适合: 读多写少的场景
一致性哈希(Consistent Hashing)
- 怎么做? 把key和服务器都映射到一个环上
- 优点: 增删节点时数据迁移量小
- 适合: 分布式系统、负载均衡
- 缺点:非常多,百度下吧
- 就像选工具箱里的工具,锤子、螺丝刀、扳手各有各的用处。不同的哈希表就是为了应对不同的实际需求而生的,永远没有完美的解决方案,永远更优的解决方案。
- 内存敏感?用开放寻址
- 要求简单稳定?用链表法
- 分布式场景?用一致性哈希
- 读操作特别多?考虑布谷鸟哈希
题外话:哈希表的前世今生与永远的更优
前世
- 1953年,IBM的Hans Peter Luhn首次提出了哈希的概念
- 真正让哈希表发扬光大的是1968年的一篇论文,作者是Robert Morris
- 当时计算机内存很贵,程序员们迫切需要一种能快速查找数据、又不占太多空间的方法
- 哈希表就是在这种背景下诞生的——用"空间换时间"的智慧
今生
- 现在几乎所有编程语言都内置了哈希表:
- Python的
dict - Java的
HashMap - JavaScript的
Object和Map - C++的
unordered_map
- Python的
- 数据库索引、缓存系统(Redis)、区块链、密码学都在用它
- LeetCode上大概有几百道题都能用哈希表
从1953年IBM的Hans Peter Luhn第一次提出哈希的概念,到今天各种花式哈希表遍地开花,这个数据结构已经走过了70多年。
每隔几年就会冒出新的变种——Robin Hood Hashing、Hopscotch Hashing、Swiss Table...工程师们像炼金术士一样,不断调整着时间、空间、复杂度之间的平衡。
也许这就是计算机科学的魅力:没有银弹,只有权衡。每一种"更优",都只是在特定场景下的"更合适"。
天才
- 笔者在写这篇博客查阅资料时,偶然看到一个挺有意思的故事。罗格斯大学有个本科生,安德鲁·克拉皮文,有一天他读到一篇叫《Tiny Pointers》的论文,突然灵光一闪:诶,这个tiny pointer的内存占用还能再优化!
- 于是他开始动手,打算用哈希表来存储tiny pointer指向的数据。结果在折腾的过程中,这哥们居然意外发现了一种速度更快的方法,这个方法,推翻了计算机科学界一个被奉为圭臬的理论——姚氏猜想。
- 1985年,图灵奖得主、著名计算机科学家姚期智在论文《Uniform Hashing Is Optimal》里说:对于某些特定类型的哈希表,最优的查找方法就是"均匀探测"(uniform probing),而且最坏情况下,插入一个元素的时间复杂度就是O(x),没法再快了。而在今年,这条铁律被打破了。
- 这相当于什么呢
- 一个业余棋手在研究残局时,发现了一个被公认为"必输"的棋局其实有破解方法,推翻了世界冠军级大师的定论。
- 一个土木工程本科生在做毕业设计时,找到了一种新的桥梁结构,突破了权威教授论文中"该跨度下的最大承重极限"。
- 一个语言学学生在研究方言时,发现了一个反例推翻了著名语言学家提出的"某类语法结构在所有人类语言中都不存在"的结论
- …………
姚期智:我用严密的数学证明这是极限。
克拉皮文:哦,我不知道,我就随便试试。
姚期智:???
- 下图为:安德鲁·克拉皮文
- 论文相关

原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。
原创声明:本文系作者授权腾讯云开发者社区发表,未经许可,不得转载。
如有侵权,请联系 cloudcommunity@tencent.com 删除。

