子数组问题——动态规划

用户11719974

发布于 2025-11-15 09:33:00

130

个人主页：敲上瘾-CSDN博客动态规划

基础dp：基础dp——动态规划-CSDN博客
多状态dp：多状态dp——动态规划-CSDN博客

一、解题技巧

区分子数组（子串）与子序列：

子数组（子串）：在数列中的一段连续的元素组成的新数列，中间不可间断。
子序列：在数列中从左往右依次挑选出元素组成的新数列，或者说在数列中随意删除一些元素后，剩下的元素组成的新数列。

用动态规划做子数组类的题时，对于状态表示我们可以直接设：

dp[i]为以i元素结尾的子数组的... ...

后面就根据具体的题目要求填写，可能是子数组的和或者子数组的积等等，无论如何都可以以i元素结尾的子数组为研究对象去思考问题，如果解决不了就尝试增加状态，但研究对象不要改变。如果还解决不了那么再考虑改变或增加研究对象。

二、最大子数组和

状态表示

如上技巧所述，我们直接设状态转移方程：

dp[i]表示：以i位置结尾的子数组的最大和。

接下来只需要去尝试是否能写出正确的状态转移方程，如果能那么状态表示就是对的。

状态转移方程：

以i位置结尾的子数组我们可以分为两种：

nums[i]单独构成一个子数组
nums[i]和以i-1结尾的最大和子数组组合成的子数组。

那么这个以i-1结尾的最大子数组的值就是一个重复子问题，我们假设在前面已经计算过了，即dp[i-1]，然后需要注意两种情况只能取一种。那么：

dp[i] = max(nums[i]+dp[i-1]，nums[i])

初始化

初始化的目的主要有两个：

保证填表的时候不越界。
保证填表的正确性。

因为这里有i-1，所以如果从0开始填表可能会越界，通常有两种解决方案：

方法一：把dp[0]初始化（即dp[0]=nums[0]），然后从dp[1]位置开始填表（即从nums[1]位置开始记录）。

方法二：开辟一个n+1的空间（n=nums.size()），让dp[0]=0（需要根据具体情况具体分析），然后从dp[1]位置开始填写，而dp[1]记录的是nums[0]的情况，也就是错开一位进行记录，所以需要注意映射关系。

这题看似方法一更简洁，但对于其他题可能需要做更复杂的边界判断。所以在做动规题时更推荐使用方法二来解决边界问题。

填表顺序

从左往右。

返回值

dp表中的最大值。

代码示例：

class Solution 
{
public:
    int maxSubArray(vector<int>& nums)
    {
        int n=nums.size(),ret=INT_MIN;
        vector<int> dp(n+1);
        for(int i=1;i<n+1;i++)
        {
            dp[i]=max(nums[i-1],nums[i-1]+dp[i-1]);
            ret=max(ret,dp[i]);
        }    
        return ret;
    }
};

三、乘积最大子数组

状态表示

同样的我们假设状态表示为：

dp[i]表示：以i位置结尾的子数组的最大乘积。

那么状态转移方程dp[i]=max(dp[i-1]*nums[i]，nums[i])，我们想一想这样对吗？比如dp[i-1]*nums[i]，nums[i]乘以一个最大积的子数组就是最大吗？

如果nums是一个负数不就变成最小乘积了吗，反之nums[i]小于0时乘以一个最小的数才能成为最大积。

所以当nums[i]小于0时我们需要知道以i-1结尾的子数组的最小积。

所以状态表示为：

f[i]表示：以i位置结尾的子数组的最大乘积。
g[i]表示：以i位置结尾的子数组的最小乘积。

状态转移方程

nums[i]>=0：
- f[i] = max(f[i-1]*nums[i]，nums[i])
- g[i] = min(g[i-1]*nums[i]，nums[i])
nums[i] < 0:
- f[i] = max(g[i-1]*nums[i]，nums[i])
- g[i] = min(f[i-1]*nums[i]，nums[i])

或：

f[i]=max(nums[i],max(nums[i]*f[i-1],nums[i]*g[i-1]));
g[i]=min(nums[i],min(nums[i]*f[i-1],nums[i]*g[i-1]));

初始化

与上一题相同，为防止越界我们给两个dp表都多开辟一个空间，映射关系错开一位。

然后把两个dp表都初始化为1，因为这里是乘法，如果使用默认的0值那么这个结果都是0。

注：dp[0]是我们为防止越界添加上的虚拟位置，它的值需要使得后面的填表正确。

填表顺序

从左往右，f表和g表一起填。

返回值

f表中的最大值。

代码示例：

class Solution {
public:
    int maxProduct(vector<int>& nums)
    {
        int n=nums.size(), ret=INT_MIN;;
        vector<int> f(n+1,1),g(n+1,1);
        for(int i=1;i<=n;i++)
        {
            f[i]=max(nums[i-1],max(nums[i-1]*f[i-1],nums[i-1]*g[i-1]));
            g[i]=min(nums[i-1],min(nums[i-1]*f[i-1],nums[i-1]*g[i-1]));
            ret=max(ret,f[i]);
        }
        return ret;
    }
};

四、最长湍流子数组

题目的核心就一句话：比较符号在子数组中的每个相邻元素对之间翻转。

然后找到满足这样的条件的最长子数组。

状态表示

假设状态表示为：

dp[i]表示：以i结尾的最长湍流子数组。

我们把数据的大小波动抽象成一条折线，如下把示例1化为折线图：

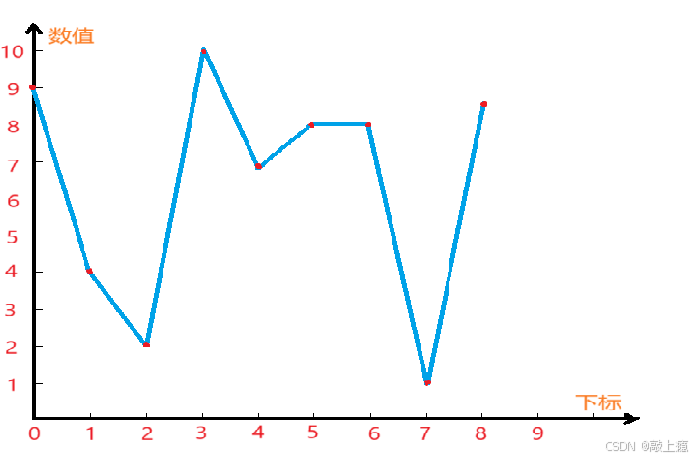
结果取该段：

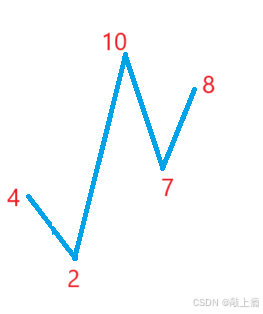
也就是子数组要满足前一个元素是上升趋势那么下一个元素必须是下降，如果前一个元素是下降趋势那么下一个元素必须是上升。

我们在做状态转移方程中主要是考虑两种情况，

nums[i]单独构成一个子数组
nums[i]接到前一个元素结尾构成的子数组中。

第2种情况又需要分情况讨论，

nums[i] < nums[i-1]：只有前面的子数组最终状态是呈现上升趋势时nums[i]才能接上。
nums[i] > nums[i-1]：只有前面的子数组最终状态是呈现下降趋势时nums[i]才能接上。
nums[i]==nums[i-1]：不能接入前面子数组。

所以我们需要把状态转移细分为两种状态：

f[i]表示：以i结尾并且最后一个元素呈上升趋势的最长湍流子数组的长度。
g[i]表示：以i结尾并且最后一个元素呈下降趋势的最长湍流子数组的长度。

状态转移方程

nums[i] < nums[i-1]：
- f[i]=1
- g[i]=f[i-1]+1
nums[i] > nums[i-1]：
- f[i]=g[i-1]+1
- g[i]=1
nums[i]==nums[i-1]：
- f[i]=1
- g[i]=1

因为任意一个子数组，最小的长度都是1，所以可以把两个dp表都初始化为1，那么状态转移方程可简化为：

nums[i] < nums[i-1]：g[i]+=f[i-1]
nums[i] > nums[i-1]：f[i]+=g[i-1]

初始化

为防止越界我们给两个dp表都多开辟一个空间，映射关系错开一位。

然后把两个dp表都初始化为1。

填表顺序

从左往右，f表和g表同时填写。

返回值

f表和g表中的最大那个元素

代码示例：

class Solution {
public:
    int maxTurbulenceSize(vector<int>& arr)
    {
        int n=arr.size(),ret=1;
        vector<int> f(n,1),g(n,1);
        for(int i=1;i<n;i++)
        {
            if(arr[i]<arr[i-1]) g[i]+=f[i-1];
            if(arr[i]>arr[i-1]) f[i]+=g[i-1];
            ret=max(ret,max(f[i],g[i]));
        }    
        return ret;
    }
};

五、单词拆分

状态表示

根据经验直接设状态表示：

dp[i]表示：从0到i位置结尾的字符串是否能被字典中的单词表示（bool类型）。

状态转移方程

因为在填写i时以前的每个子串是否能由字典表示已经知道，储存在dp表中。那么我们只需要找到任意一个j（0<=j<i）使得dp[j]=true，并且子字符串[j+1，i]能用字典表示，那么dp[i]=true，否则dp[i]=false。

所以状态转移方程：

dp[i] = (dp[i-1]&&s[i，i]能用字典表示) || (dp[i-2]&&s[i-1，i]能用字典表示) || ... ... ||(dp[0]&&s[1，i]能用字典表示)

注：s[i-1，i]表示字符串中i-1到i这个子串。

初始化

为了让第一个字符元素也讨论进来，我们创建n+1的dp表，并把dp[0]初始化为true。

填表顺序

从左往右

返回值

return dp[n]

代码示例：

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict)
    {
        int n=s.size();
        unordered_set<string> st(wordDict.begin(),wordDict.end());
        vector<bool> dp(n+1);
        dp[0]=true;
        for(int i=1;i<=n;i++)
        {
            for(int j=0;j<i;j++)
            {
                if(dp[j]==false) continue;
                if(st.count(string(s.begin()+j,s.begin()+i)))
                {
                    dp[i]=true;
                    break;
                }
            }
        }   
        return dp[n];
    }
};

好题推荐：