多状态dp——动态规划

在阅读该文章时最好对基础的动态规划有所了解，因为在此不会讲解动态规划基础的细节，大家可以通过阅读下文进行学习： 基础dp——动态规划-CSDN博客

一、多状态dp与一般dp的区别

• 一般DP：每个状态通常保存单一的最优值。例如，斐波那契数列中 dp[i] 仅表示第 i 项的值。
• 多状态DP：每个状态点需要维护多个子状态，分别表示不同情境下的最优解。例如，股票买卖问题中，每个时间点需记录「持有股票」和「未持有股票」两种状态下的最大收益。

二、理解多状态DP

1. 状态分解：将问题划分为多个互相影响的状态。例如：
   • 股票问题：持有、未持有、冷冻期。
   • 粉刷房子：当前房子涂红、蓝、绿时的最小成本。
2. 状态转移：每个子状态的值需根据前一步其他子状态计算。例如：
   • 当天持有股票的最大收益 = max(前一天已持有继续持有， 前一天未持有当天买入)。
3. 最终解：通常取结尾多个子状态中的最优值。

三、解题步骤

1. 识别子状态：明确问题中需要区分的状态类型。并定义DP数组。
2. 状态转移方程：为每个子状态写出转移关系。
3. 初始化：设置初始步骤各子状态的值。
4. 递推计算：按顺序填充DP表，确保无循环依赖。
5. 提取结果：从最终状态的子状态中选择最优解。

四、试题讲解

1.打家劫舍

状态表示：

假设我们按之前的经验，使用dp[i]表示从0到i能偷窃到的最高金额。并试着写出状态转移方程。而我们只知道dp[i-1]是0到i-1能偷窃的最高金额，我们也不能直接使用，因为题目明确要求两房间之间不能连续偷窃。我们不知道dp[i-1]中i-1房间是否偷窃，那就无法决策到i房间时是否偷窃。

一个房间是可以选择偷和不偷的，也就是有两个状态，所以我们可以创建n*2的dp表，这个2表示有两个状态，如下：

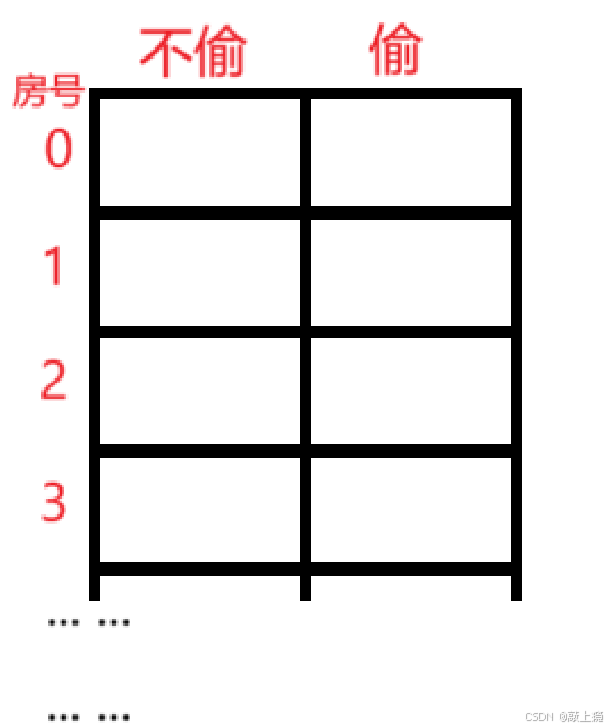
即：

• dp[i][0]表示：偷到i，不偷nums[i]，此时偷窃的最大金额。
• dp[i][1]表示：偷到i，偷取nums[i]，此时偷窃的最大金额。

状态转移方程

• dp[i][0]=max(dp[i-1][0]，dp[i-1][0])
• dp[i][1]=nums[i]+dp[i-1][0]

初始化

dp[0][0]=0，dp[0][1]=nums[0]

填表顺序

从1下标开始，并从左往右填写。

返回值

return max(dp[n-1][0]，dp[n-1][1])

代码示例：

class Solution {
public:
    int rob(vector<int>& nums)
    {
        int n=nums.size();
        vector<vector<int>> dp(n,vector<int>(2));
        dp[0][1]=nums[0];
        for(int i=1;i<n;i++)
        {
            dp[i][0]=max(dp[i-1][0],dp[i-1][1]);
            dp[i][1]=dp[i-1][0]+nums[i];
        }    
        return max(dp[n-1][0],dp[n-1][1]);
    }
};

类似题型：213. 打家劫舍 II - 力扣（LeetCode）提示：把环形问题拆分成两个线性的“打家劫舍I”。

具体操作：把0号房拆分成选和不选，选0号房：在[2，n-2]区间做dp。不选0号房：在[1,n-1]区间做dp。然后选择两者最优。

2.粉刷房子

该题的思想和上题是一模一样的，同样需要多个状态来表示该墙面刷某颜色时的最小花费。

状态表示：

即：

• dp[i][0]表示：刷到i，并把i墙刷为红色，此时花费的最小金额。
• dp[i][1]表示：刷到i，并把i墙刷为蓝色，此时花费的最小金额。
• dp[i][2]表示：刷到i，并把i墙刷为绿色，此时花费的最小金额。

状态转移方程

• dp[i][0]=cost[i][0]+min(dp[i-1][1]，dp[i-1][2])
• dp[i][1]=cost[i][1]+min(dp[i-1][0]，dp[i-1][2])
• dp[i][2]=cost[i][2]+min(dp[i-1][0]，dp[i-1][1])

初始化

这里为了方便，我们可以不用单独初始化，在创建dp表时创建一个(n+1)*3的，然后让1下标来表示第0面墙，所以需要注意下标的映射关系。

填表顺序

从1下标开始，并从左往右填写。

返回值

return max(dp[n][0]，dp[n][1]，dp[n][2])

代码示例：

class Solution {
public:
    int minCost(vector<vector<int>>& costs)
    {
        int n=costs.size();
        vector<vector<int>> dp(n+1,vector<int>(3,0));
        for(int i=1;i<=n;i++)
        {
            dp[i][0]=min(dp[i-1][2],dp[i-1][1])+costs[i-1][0];
            dp[i][1]=min(dp[i-1][0],dp[i-1][2])+costs[i-1][1];
            dp[i][2]=min(dp[i-1][0],dp[i-1][1])+costs[i-1][2];
        }
        return min(dp[n][0],min(dp[n][1],dp[n][2]));
    }
};

3.买卖股票问题

通过前两题的经验，首先我们直接来看第i天可能有的状态，而这些状态并不是简单的“买入”，“卖出”，“冷冻期”，而是要看看能否推出正确的状态转移方程，需要结合具体情况。比如这里我们可以设它为这三种状态：“买入”，“可交易”，“冷冻期”。

注意：这里的状态针对的是整个股票而言，而不是说就是当天买入的。那么状态之间的转换如下：

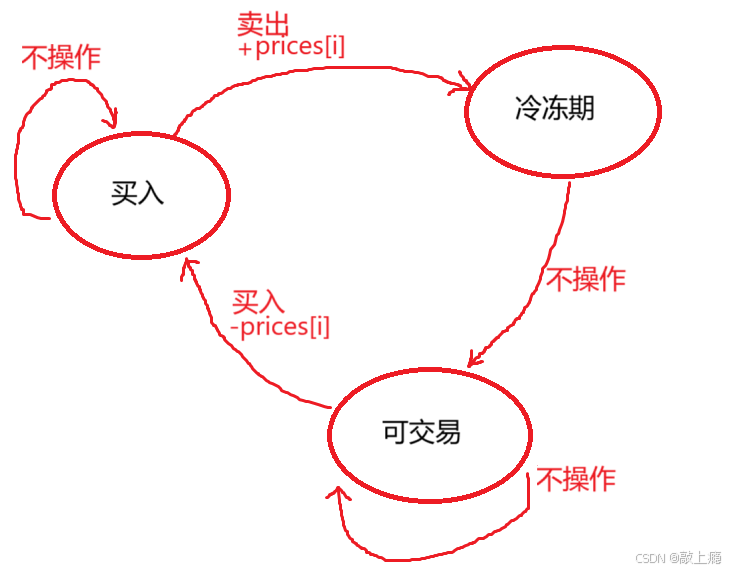
状态表示

• dp[i][0]表示：到第i天为买入状态时，此时最大利润。
• dp[i][1]表示：到第i天为可交易状态时，此时最大利润。
• dp[i][2]表示：到第i天为冷冻状态时，此时最大利润。

状态转移方程

• dp[i][0]=max(dp[i-1][0]，dp[i-1][1]-prices[i])
• dp[i][1]=max(dp[i-1][1]，dp[i-1][2])
• dp[i][2]=dp[i-1][0]+prices[i]

初始化

因为状态转移方程中用到i-1，所以为防止越界，我们需要把0位置初始化，然后从1位置开始遍历。

这里只需要dp[0][0]=-prices[0]即可。

填表顺序

从1下标开始，并从左往右填写。

返回值

因为dp[n-1][0]必然比其他两个小，所以

return max(dp[n-1][1]，dp[n-1][2])

代码示例

class Solution {
public:
    int maxProfit(vector<int>& prices)
    {
        int n=prices.size();
        vector<vector<int>> dp(n,vector<int>(3));
        dp[0][0]=-prices[0];
        for(int i=1;i<n;i++)
        {
            dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]);
            dp[i][1]=max(dp[i-1][1],dp[i-1][2]);
            dp[i][2]=dp[i-1][0]+prices[i];
        }    
        return max(dp[n-1][1],dp[n-1][2]);
    }
};

这个题很容易能想到的两个状态：“买入”，“卖出”。但是这个两个状态还不足以让我们写出正确的状态转移方程。题目还有一个限制要求：最多只能做两笔交易，所以还需要知道已经做了几个交易。即在上面两个状态的基础上还分别需要三个子状态：“已完成0笔交易”，“已完成1笔交易”，“已完成2笔交易”。

状态表示

• j = 0,1,2
• dp[ i ][ 0 ][ j ]表示：到第i天结束后，并且第i天为买入，此时完成 j 笔交易状态下的最大收益。
• dp[ i ][ 1 ][ j ]表示：到第i天结束后，并且第i天为卖入，此时完成 j 笔交易状态下的最大收益。

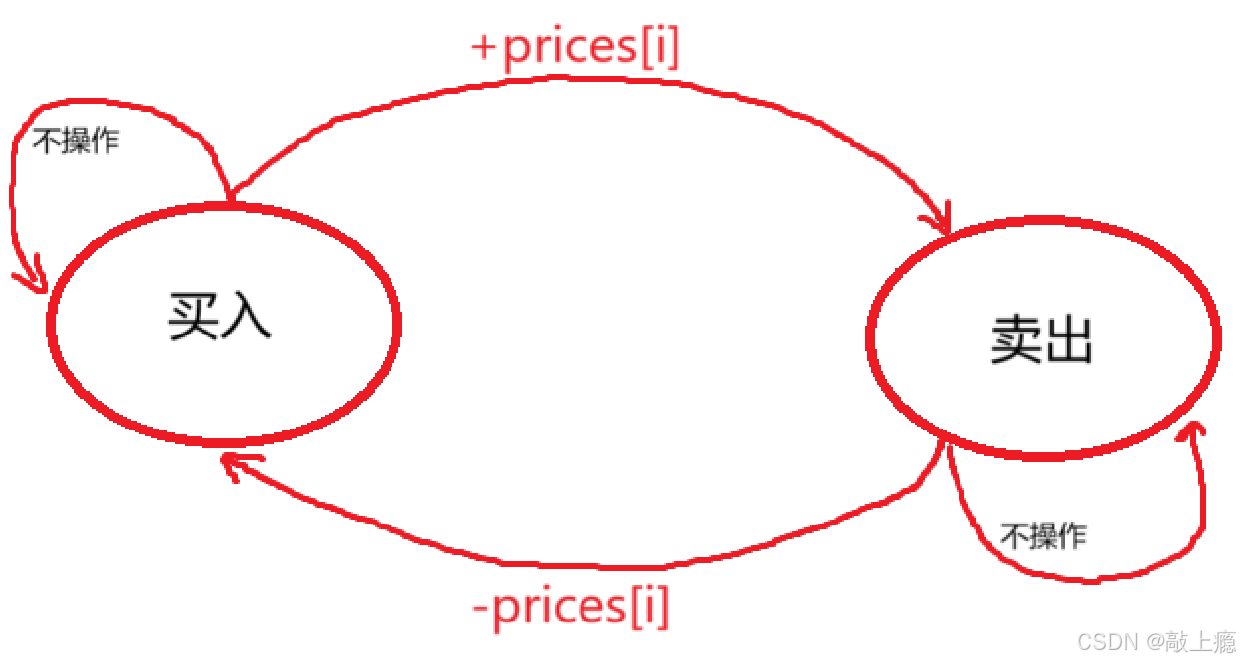
状态转移方程

• dp[i][0][j]=max(dp[i-1][0][j]，dp[i-1][1][j]-prices[i])
• dp[i][1][j]=max(dp[i-1][0][j-1]+prices[i]，dp[i-1][1][j])

初始化

首先dp[0][0][0]=-prices[0]，dp[0][1][0]=0，而其他状态都是非法的，比如0天就完成交易1次，2次。所以为了防止在状态转移方程中被选中，可以把它们都设为无穷小。而为了防止数字太小而溢出，我们把它设为-0x3f3f3f3f。

填表顺序

从左到右

返回值

因为最佳利润绝对不会在买入状态，所以我们从dp[n-1][1][j]中找到最佳利润并返回。

代码示例：

class Solution {
public:
    int maxProfit(vector<int>& prices)
    {
        int n=prices.size();
        vector<vector<vector<int>>> dp(n,vector<vector<int>>(2,vector<int>(3,-0x3f3f3f3f)));
        dp[0][0][0]=-prices[0],dp[0][1][0]=0;
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<3;j++)
            {
                dp[i][0][j]=max(dp[i-1][0][j],dp[i-1][1][j]-prices[i]);
                if(j-1>=0) dp[i][1][j]=max(dp[i-1][1][j],dp[i-1][0][j-1]+prices[i]);
                else dp[i][1][j]=dp[i-1][1][j];
            }
        }
        int ret=0;
        for(int j=0;j<3;j++) ret=max(ret,dp[n-1][1][j]);
        return ret;
    }
};

买卖股票类型好题推荐：

121. 买卖股票的最佳时机 - 力扣（LeetCode）

122. 买卖股票的最佳时机 II - 力扣（LeetCode）

123. 买卖股票的最佳时机 III - 力扣（LeetCode）

188. 买卖股票的最佳时机 IV - 力扣（LeetCode）

714. 买卖股票的最佳时机含手续费 - 力扣（LeetCode）

309. 买卖股票的最佳时机含冷冻期 - 力扣（LeetCode）