30 分钟掌握 STL容器

Part 01 提出问题：30 分钟掌握 STL

本文 分为三部分

•

STL有那些容器，各自使用场景

•

STL容器底层结构和时间复杂度

•

STL关键特性和部分源码分析

1. STL有那些容器，各自使用场景

•

请简述STL中顺序容器、关联容器、无序关联容器和容器适配器各有哪几种？

•

在以下场景中，你会选择哪种STL容器？请阐述理由。

2. STL容器底层结构和时间复杂度

•

vector 底层机制是什么？如何避免动态扩容

•

map 和 unordered_map 底层数据结构分别是什么？当数量大时候，最坏情况是时间复杂度多少？最坏情况性能（哈希冲突时O(n) 如何避免

•

sort 采用那个时间复杂度多少？如何实现的

3. STL关键特性和具体实现

•

stl 容器 迭代器，算法之间关系？

•

偏特化和萃取机制 模版关系？

•

移动语义 和模版 萃取有什么关系？

打卡输出

依赖准备：

SGI STL 是侯捷老师最推荐的可读性最高的一种STL实现。 GCC 中用的就是这个版本的实现。

了解:

数据结构可视化演示平台

•

https://visualgo.net/zh

•

https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

Part 02 数据结构和时间复杂度

2.1 std::priority_queue

1. 了解：你知道 ，别人也知道

std::priority_queue 容器适配器底层就虽然底层是 vector，连续的数组 https://en.cppreference.com/w/cpp/container/priority_queue.html

template<
    class T,
    class Container = [std::vector]
    class Compare = [std::less]
> class priority_queue

但是堆也是通过数组来实现的，如图

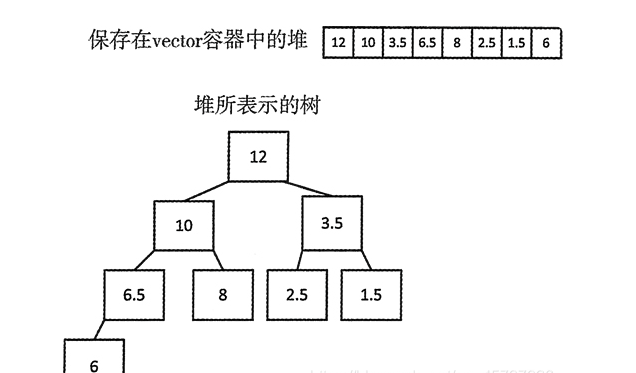
大顶堆

算法

代码位置：

•

https://github.com/karottc/sgi-stl/blob/master/stl_queue.h

sgi-stl/ ├── stl_heap.h # priority_queue 的核心实现（堆算法） ├── stl_queue.h # priority_queue 的类定义和接口 ├── heap.h # 可能包含堆算法（某些版本） └── algorithm # 包含堆相关的算法

pop_heap`实际上执行两个关键操作：

1

交换堆顶元素与末尾元素

2

重新调整剩余元素以维持堆性质

https://github.com/karottc/sgi-stl/blob/master/stl_queue.h

void pop() { try { pop_heap(c.begin(), c.end(), comp); // 将最大元素移到末尾 O(log n) c.pop_back(); // 删除末尾元素 } catch(...) { c.clear(); throw; } }

让我用一个真实例子展示 `pop_heap` 到底在做什么。假设我们有一个最大堆，存储着这些数字：**初始堆：** [9, 5, 8, 2, 3, 7, 6]``` shell        9       / \      5   8     / \ / \    2  3 7  6

现在调用 pop_heap(v.begin(), v.end())：

第一步：交换堆顶和末尾 把根节点9和最后一个节点6交换位置：

        6  ← 新的根节点（临时）
       / \
      5   8
     / \ / \
    2  3 7  9  ← 原来的堆顶现在在末尾

数组变成：[6, 5, 8, 2, 3, 7, 9] 最后一个位置不是堆的范围了

第二步：向下调整堆 从新的根节点6开始，与较大的子节点8比较，6 < 8，所以交换：

        8  ← 调整后的根节点
       / \
      5   6  ← 6下沉到这里
     / \ / \
    2  3 7  9

数组变成：[8, 5, 6, 2, 3, 7, 9]

第三步：继续调整 检查6的位置，它的子节点是7，6 < 7，继续交换：

        8       / \      5   7  ← 7比6大，交换     / \ / \    2  3 6  9

最终数组：[8, 5, 7, 2, 3, 6, 9]

vector<int> data = {9, 5, 8, 2, 3, 7, 6};
make_heap(data.begin(), data.end());  // 建堆

// 弹出堆顶
pop_heap(data.begin(), data.end());   // 9被移到末尾，前n-1个元素重新调整成堆
data.pop_back();                      // 真正删除原来的堆顶元素9

push 操作 回忆 堆操作 （1） 建堆 （2） 调整堆

https://en.cppreference.com/w/cpp/container/priority_queue/push.html
https://github.com/karottc/sgi-stl/blob/master/stl_queue.h
void push(const value_type& __x) {
    try {
        c.push_back(__x);              // 先将元素加入底层容器
        push_heap(c.begin(), c.end(), comp);  // 然后调整堆结构
    } catch(...) {
        c.clear();
        throw;
    }
}
说明：sort_heap 是排序算法 在这里不用

push_heap 的过程，使用示例 {9, 5, 8, 2, 3, 7, 6}。

初始最大堆： [9, 5, 8, 2, 3, 7, 6]

        9
       / \
      5   8
     / \ / \
    2  3 7  6

第一步：手动添加新元素 假设我们要添加元素 10，先执行 data.push_back(10)： 数组变成：[9, 5, 8, 2, 3, 7, 6, 10]

此时的树结构（暂时破坏堆性质）：

        9
       / \
      5   8
     / \ / \
    2  3 7  6
   /
  10  ← 新元素，但位置不对

第二步：调用 push_heap 进行调整 现在调用 push_heap(data.begin(), data.end())，开始向上调整：

调整过程：

1

新元素10在索引7，其父节点在索引(7-1)/2=3，即元素2

2

10 > 2，所以交换位置：

        9
       / \
      5   8
     / \ / \
    10 3 7  6  ← 10上浮一层
   /
  2

数组：[9, 5, 8, 10, 3, 7, 6, 2]

1

10现在在索引3，其父节点在索引(3-1)/2=1，即元素5

2

10 > 5，继续交换：

        9
       / \
      10  8
     / \ / \
    5  3 7  6  ← 10继续上浮
   /
  2

数组：[9, 10, 8, 5, 3, 7, 6, 2]

1

10现在在索引1，其父节点在索引(1-1)/2=0，即根节点9

2

10 > 9，继续交换：

        10
       / \
      9   8
     / \ / \
    5  3 7  6  ← 10到达堆顶
   /
  2

数组：[10, 9, 8, 5, 3, 7, 6, 2]

最终结果： 新元素10经过3次比较和交换，从叶子节点一路上浮到堆顶，重新构成了有效的最大堆。

关键要点：

•

push_heap 不添加元素，只负责调整堆结构

•

调整过程是自底向上的，新元素不断与父节点比较并上浮

•

时间复杂度是 O(log n)，因为只需要沿着树的高度向上调整

（完整代码示例）

vector<int> data = {9, 5, 8, 2, 3, 7, 6};
make_heap(data.begin(), data.end());  // 先建堆

// 添加新元素并调整堆
data.push_back(10);                   // 先手动添加
push_heap(data.begin(), data.end());  // 再调整堆结构

为什么是 O(log n) 而不是 O(n)：

•

堆的树形结构决定了调整路径的长度

•

即使有100万个元素，堆的高度也只有约20层

•

最坏情况下也只需要20次比较，不会随着数据量线性增长

第一步：添加元素 - O(1) data.push_back(10) 只是简单地在数组末尾添加元素

第二步：向上调整堆 - O(log n) 这是 push_heap 的核心操作，新元素10需要从叶子节点向上"浮动"到正确位置：

1

第一次比较：10 vs 父节点2 → 交换 (10 > 2)

2

第二次比较：10 vs 父节点5 → 交换 (10 > 5)

3

第三次比较：10 vs 父节点9 → 交换 (10 > 9)

总共进行了 3次比较和交换，正好等于树的高度。

时间复杂度证明：

•

堆是一个完全二叉树，有n个元素的堆高度是 log₂n

•

最坏情况下，新元素需要从最底层一直浮动到根节点

•

每次浮动只需要与父节点比较一次

•

所以时间复杂度是 O(log n)

数据量   堆高度   push_heap最坏情况

8       3       3次比较

16      4       4次比较

1024    10      10次比较

100万   20      20次比较

场景基本操作

void testHeap() {
    vector<int> data{ 3,1,2,7,5 };
    //构造堆，最大堆
    make_heap(data.begin(), data.end(), less<int>());
    //pop堆顶元素，最大的元素
    pop_heap(data.begin(), data.end(), less<int>());
    cout << data.back() << endl;//输出7
    data.pop_back();
  是vector的末尾。
（4）sort_heap()对整个堆排序

std::priority_queue 的本质是一个容器适配器（Container Adapter），

它通过依赖底层容器（如 vector或 deque）来存储数据，并利用 make_heap、push_heap、pop_heap这一系列泛型算法来在底层容器上维护堆结构，从而提供优先级队列的接口和行为

STL 第一个特性 技术 容器 和算法 集合

make_heap

 priority_queue(const _Compare& __x, const _Sequence& __s)
    : c(__s), comp(__x)
    { make_heap(c.begin(), c.end(), comp); }


vector<int> data = {3, 1, 4, 1, 5, 9, 2, 6};
make_heap(data.begin(), data.end());  // 线性时间建堆
cout << "最大堆顶: " << data.front() << endl;  // 输出9

初始数组： [3, 1, 4, 1, 5, 9, 2, 6]

        3       / \      1   4     / \ / \    1  5 9  2   /  6

make_heap 的核心思想是自底向上构建堆，从最后一个非叶子节点开始向前调整。

构建过程详解：

第一步：找到调整起点 最后一个非叶子节点的索引 = (n/2) - 1 = (8/2) - 1 = 3 所以从索引3（值为1）开始调整

第二步：调整索引3（值为1）

        3       / \      1   4     / \ / \    1  5 9  2   ← 索引3的1不需要调整（没有右子节点，且1 > 6？不对，左子节点是6）   /  6

实际上索引3的节点1有左子节点6（索引7），1 < 6，需要交换：

        3       / \      1   4     / \ / \    6  5 9  2   /  1

数组变为：[3, 1, 4, 6, 5, 9, 2, 1]

第三步：调整索引2（值为4） 4的子节点是9和2，4 < 9，交换：

        3       / \      1   9     / \ / \    6  5 4  2   /  1

数组变为：[3, 1, 9, 6, 5, 4, 2, 1]

第四步：调整索引1（值为1） 1的子节点是6和5，1 < 6，交换：

        3       / \      6   9     / \ / \    1  5 4  2   /  1

现在1在索引3，需要继续向下调整。1的子节点是1（索引7），1 >= 1，停止。 数组变为：[3, 6, 9, 1, 5, 4, 2, 1]

第五步：调整索引0（值为3） 3的子节点是6和9，3 < 9，交换：

        9       / \      6   3     / \ / \    1  5 4  2   /  1

现在3在索引2，需要继续调整。3的子节点是4和2，3 < 4，交换：

        9       / \      6   4     / \ / \    1  5 3  2   /  1

数组变为：[9, 6, 4, 1, 5, 3, 2, 1]

最终最大堆： [9, 6, 4, 1, 5, 3, 2, 1]

        9       / \      6   4     / \ / \    1  5 3  2   /  1

make_heap建堆时间复杂度

时间复杂度分析

时间复杂度：O(n)，而不是直觉上的 O(n log n)

为什么是 O(n)？

考虑完全二叉树：

•

有 n/2 个叶子节点（高度为0）：不需要调整

•

有 n/4 个节点高度为1：最多调整1次

•

有 n/8 个节点高度为2：最多调整2次

•

...

•

有 1 个根节点高度为 h：最多调整 h 次

总操作次数：

T(n) = n/4 * 1 + n/8 * 2 + n/16 * 3 + ... + 1 * h     < n * (1/4 + 2/8 + 3/16 + ...)     = O(n)

#STL面试 #C++进阶 #大厂面试 #程序员成长 #分布式存储

别人知道：你不知道 堆时间复杂度

问：大顶堆获取最大值 时间复杂度多少 o(1)

问：大顶堆获取最小值呢 ，倒数第二小， 时间复杂度多少 ？

根据堆性质 ，

•

一次堆调整 只能保证 根节点是最大的，根的兄弟之间无法判断大小的。【这里不是不是搜索树，每个这个特性】

•

但是 清楚，叶子几点很多是最小的，n/2 --n 之间。

让我用具体例子说明。 假设大顶堆：[9, 6, 8, 3, 5, 7, 1]

        9
       / \
      6   8
     / \ / \
    3  5 7  1  ← 最小值1，第二小可能是3

为什么还是 O(n)：

要找第二小的值，你不能简单地找到最小值就停止，因为：

1

你需要找到最小的两个值

2

第二小的值可能在任何位置，不一定紧挨着最小值

3

可能存在重复的最小值

查找过程：

vector<int> max_heap = {9, 6, 8, 3, 5, 7, 1};
int min1 = INT_MAX;  // 最小值
int min2 = INT_MAX;  // 第二小值

// 必须遍历整个堆，同时跟踪最小的两个值
for(int i = 0; i < max_heap.size(); i++) {
    if(max_heap[i] < min1) {
        min2 = min1;  // 原来的最小值变成第二小
        min1 = max_heap[i];  // 更新最小值
    } else if(max_heap[i] < min2 && max_heap[i] != min1) {
        min2 = max_heap[i];  // 更新第二小值
    }
}
// 最终 min1=1, min2=3

特殊情况处理：

•

如果最小值有重复，比如堆中有两个1，那么第二小值就是1

•

如果堆中所有元素都相同，那么最小值和第二小值相同

•

如果堆只有一个元素，那么没有第二小值

时间复杂度分析：

•

必须遍历所有 n 个元素

•

每个元素最多比较2次

•

总体时间复杂度 O(n)

堆：合理的疑问，倒数第二小值 为什么不是一定在叶子节点吗？

为什么必须遍历所有 n 个元素？

•

堆结构限制：大顶堆只保证根节点是最大值，但最小值和第二小值可能出现在任何位置，包括内部节点或叶子节点。如果只遍历叶子节点（大约 n/2 个），可能会错过内部节点中的较小值。

•

示例分析：考虑一个大顶堆 [10, 2, 9, 1, 3, 8, 7]，其树结构如下

      10
     /  \
    2    9
   / \  / \
  1  3 8  7

你在STL源码分析中还遇到过哪些难题？欢迎在评论区讨论。

发散 堆排序，快速排序 计算top k时间复杂度多少，能优化吗？

审题： 计算 top k ，只要第 k 个就可以了，不需要全部排序

我们要找出数组中前 K 大（或前 K 小）的元素， 核心思想是：不必完全排序，只要确定 “第 K 个元素” 的位置即可。 这时 QuickSort 可以 “剪枝” —— 每次只递归到一边。

// C++ 风格示意
int quickselect(vector<int>& a, int l, int r, int k) {
    int pivot = partition(a, l, r); // 快排中的 partition
    int cnt = r - pivot + 1; // pivot 右侧元素数量
    if (cnt == k) return a[pivot];
    else if (cnt > k) return quickselect(a, pivot+1, r, k);
    else return quickselect(a, l, pivot-1, k - cnt);
}

快速选择算法基于快速排序的分区思想，

但关键区别在于它只递归处理包含目标元素的那一侧，而不是像快速排序那样处理两侧

设总数据量为n，则递归调用序列为：

•

第一次分区：处理n个元素

•

第二次分区：处理约n/2个元素

•

第三次分区：处理约n/4个元素

•

...

T(n) = O(n) + O(n/2) + O(n/4) + ... = O(n × (1 + 1/2 + 1/4 + 1/8 + ...)) = O(n × 2) = O(n)

总操作次数 = n + n/2 + n/4 + n/8 + ... ≈ 2n

2.2 std::unordered_map 和 map find 时间复杂多少

https://github.com/karottc/sgi-stl/blob/master/stl_hashtable.h

SGI STL的hashtable通过开链法实现， 查找操作在平均情况下非常高效（O(1)），

但其性能依赖于哈希函数的质量和合理的负载因子。

在最坏情况下，查找性能会下降（O(n)）

这个情况该如何优化？

•

Java 8+的HashMap 在桶的链表过长时转换为红黑树

•

Java 的 ConcurrentSkipListMap 是一个 并发跳表 实现

为什么 Redis 选跳表

1

支持有序操作：跳表天然支持范围查找、按排名取值、按 score 排序等，这正是有序集合（ZSET）所需。

2

实现简单且高效：比红黑树实现更清晰、代码更短、易于维护。

3

便于维护排名信息：跳表通过 span 字段天然支持 O(log n) 的按排名定位（这是平衡树要额外维护子树大小等信息的替代方案）。

Part 3 机制

请参考：课件

•

https://github.com/ZachL1/Bilibili-plus/blob/master/C%2B%2B-STL-HouJie/slide/Slide.pdf

3.1 迭代器与萃取

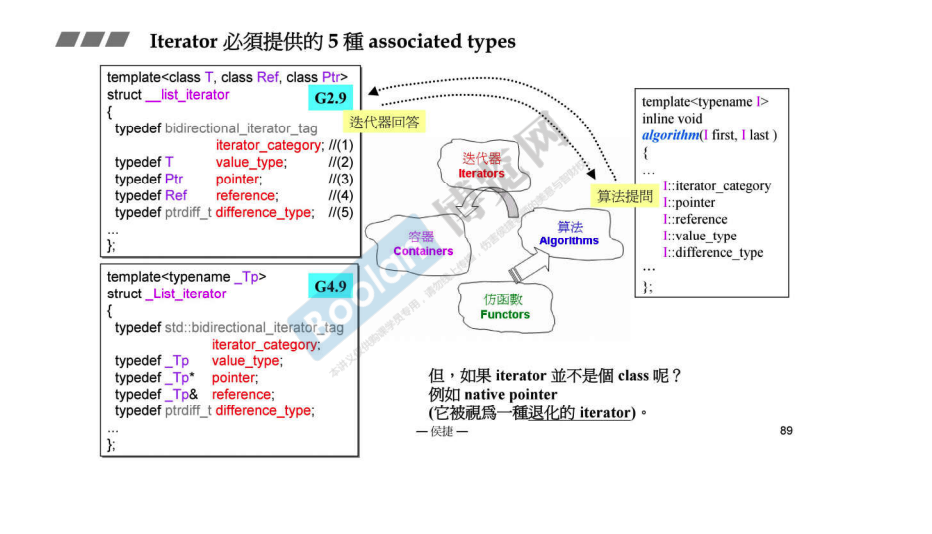
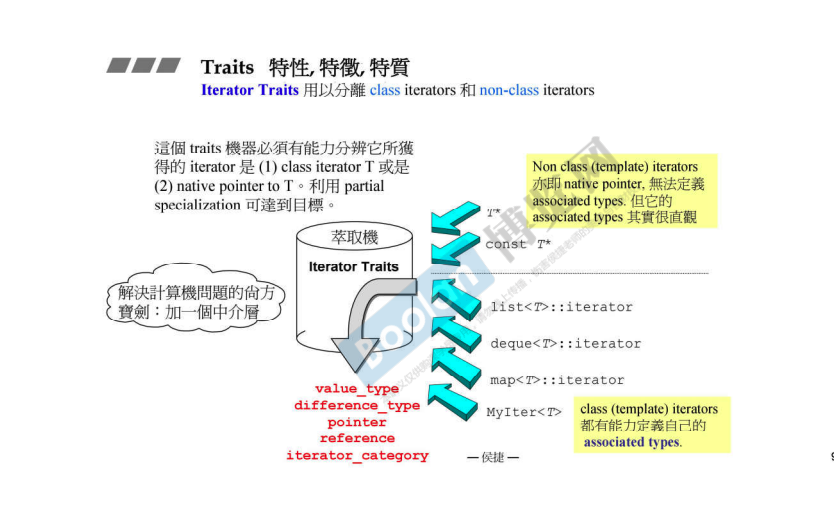
image.png

image.png

迭代器：扮演容器与算法之间的桥梁，是所谓的 “泛型指针”

native pointer 也是一种迭代器

既能处理 class iterator，也能处理 pointer iterator。 这就是 iterator_traits 登场的原因

主要功能：

•

提供迭代器的标准化类型信息接口

•

让算法无需关心迭代器的具体实现细节

•

支持指针也能作为迭代器使用

template <class T>
struct iterator_traits<T*> {
    typedef T value_type;
    typedef T* pointer;
    typedef T& reference;
    typedef ptrdiff_t difference_type;
    typedef random_access_iterator_tag iterator_category;
};

#include <iterator>
#include <type_traits>

int main() {
    using traits = std::iterator_traits<int*>;
    static_assert(std::is_same_v<traits::value_type, int>);
    static_assert(std::is_same_v<traits::pointer, int*>);
    static_assert(std::is_same_v<traits::reference, int&>);
    static_assert(std::is_same_v<traits::difference_type, std::ptrdiff_t>);
    static_assert(std::is_same_v<traits::iterator_category, std::random_access_iterator_tag>);
}

template<typename Iterator>
void process_range(Iterator first, Iterator last) {
    // 这个算法既能接受 vector<int>::iterator
    // 也能接受 int*，因为两者都有相同的 traits 接口
    using value_type = typename iterator_traits<Iterator>::value_type;
    // ...
}

// 使用示例
std::vector<int> vec = {1, 2, 3};
int arr[] = {1, 2, 3};

process_range(vec.begin(), vec.end());  // 迭代器
process_range(arr, arr + 3);           // 原生指针 ✅

提示： c struct 为不支持继承

3.2 算法

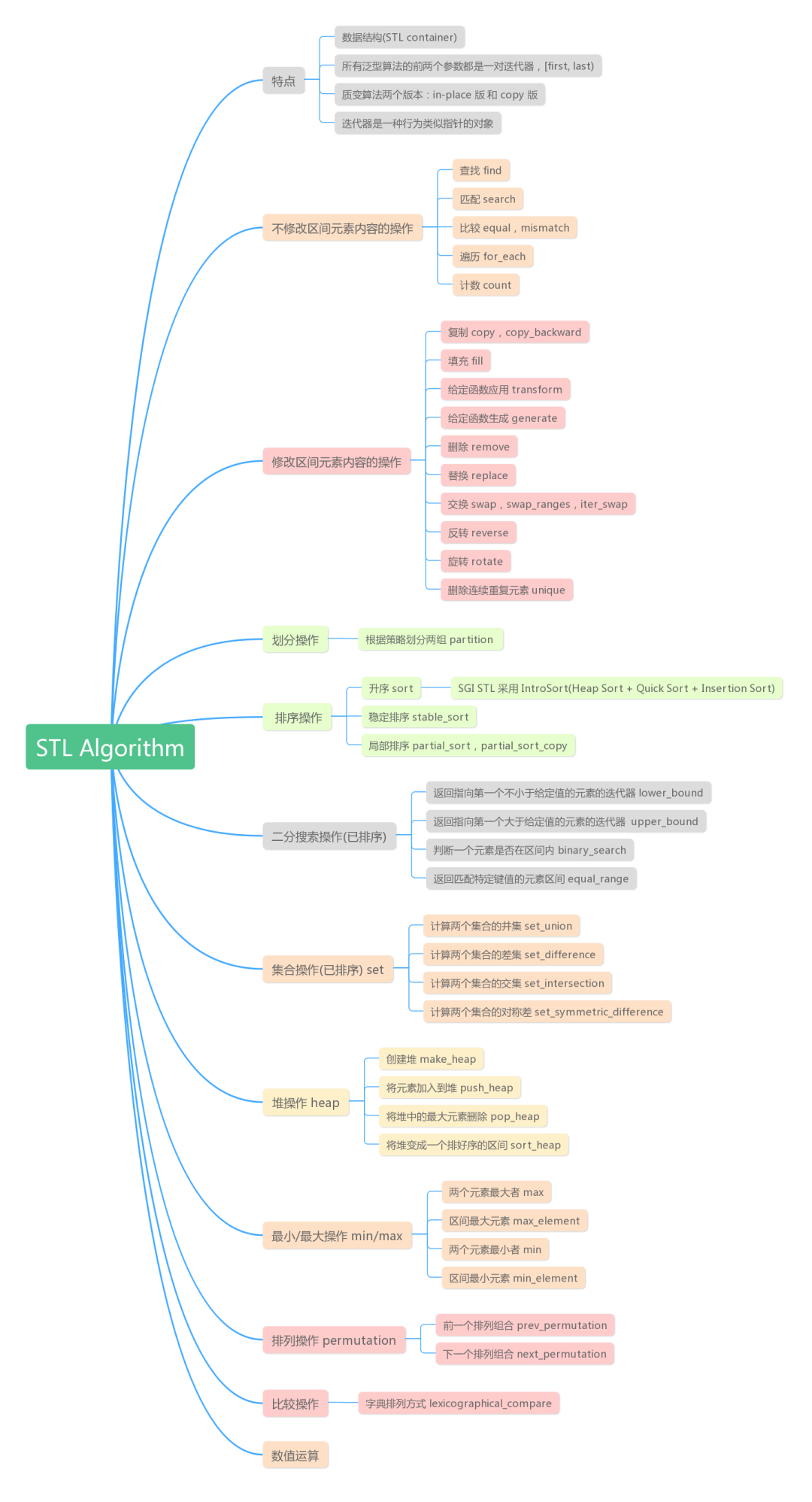
https://github.com/steveLauwh/SGI-STL/blob/master/The%20Annotated%20STL%20Sources%20V3.3/algorithm/README.md

https://github.com/steveLauwh/SGI-STL/blob/master/The%20Annotated%20STL%20Sources%20V3.3/algorithm/README.md

3.3 编译期优化

3.4 移动语义 和萃取关系

std::move

概念

•

std::move 并不会移动对象，它只是 将左值转换为右值引用。

•

用于触发移动构造函数或移动赋值运算符。

标准实现（C++17/20）

一般在 <utility> 头文件中：

namespace std {

template <class T>
constexpr typename remove_reference<T>::type&& move(T&& t) noexcept {
    return static_cast<typename remove_reference<T>::type&&>(t);
}

} // namespace std

分析：

•

remove_reference<T>::type 去掉引用。

•

然后通过 static_cast<...&&> 转换为右值引用。

typename std::remove_reference<T>::type

背景

C++ 中，模板参数 T 可能是：

•

普通类型：int

•

左值引用类型：int&

•

右值引用类型：int&&

在做 移动语义 或 完美转发 时，我们常常希望去掉引用类型，得到原始的“裸类型”。

std::remove_reference

这是一个 类型萃取 (type trait)，定义在 <type_traits> 中：

template<typename T> struct remove_reference      { typedef T type; };
template<typename T> struct remove_reference<T&>  { typedef T type; };
template<typename T> struct remove_reference<T&&> { typedef T type; };

分析：

int

也就是说，不管传入的是左值引用还是右值引用，它都去掉了引用符号，得到“原始类型”。

为什么在 std::move 中要用它？

template <class T>
constexpr typename remove_reference<T>::type&& move(T&& t) noexcept {
    return static_cast<typename remove_reference<T>::type&&>(t);
}

步骤拆解：

1

T&& t 是一个 万能引用（Forwarding Reference），可能是左值也可能是右值。

2

我们想把它转成右值引用触发移动构造：

•

如果 T 是 int&（传入的是左值），T&& → int& && → 折叠规则 → int&

•

如果 T 是 int（传入的是右值），T&& → int&&

3

所以我们先用 remove_reference<T>::type 去掉引用，得到原始类型。

4

然后再加上 && → 转成右值引用。

int x = 5;
int&& y = std::move(x);  // x 是左值

std::string s1 = "hello";
std::string s2 = std::move(s1);  // move触发的是 std::string 的移动构造函数

执行流程：

1

std::move(s1) → 编译期完成类型转换，得到 std::string&&

2

s2 调用 移动构造函数：

•

把 s1 内部指针、容量等资源直接转移给 s2

•

s1 变成空状态（不再持有原资源）

总结：

•

std::move 只是告诉编译器“把这个对象当右值使用”

•

真正的移动操作发生在 移动构造函数或移动赋值运算符 调用时（运行期）

2. std::forward

概念

•

std::forward 用于 完美转发。

•

保留传入参数的值类别（左值或右值）。

标准实现（C++17/20）

也在 <utility> 头文件中：

namespace std {

template <class T>
constexpr T&& forward(typename remove_reference<T>::type& t) noexcept {
    return static_cast<T&&>(t);
}

template <class T>
constexpr T&& forward(typename remove_reference<T>::type&& t) noexcept {
    static_assert(!is_lvalue_reference<T>::value, "bad forward");
    return static_cast<T&&>(t);
}

} // namespace std

分析：

•

forward<T> 根据模板参数 T 判断 t 是左值还是右值。

•

static_cast<T&&> 保持原始类型属性：

•

如果 T 是 U& → 左值引用

•

如果 T 是 U → 右值引用

•

常和 万能引用（T&&） 搭配使用，实现在模板中参数的完美转发。

参考

1. 侯捷C++系列视频

•

https://github.com/ZachL1/Bilibili-plus

•

https://linux.do/t/topic/448148

•

https://blog.51cto.com/binghe001/5245835

•

https://github.com/steveLauwh/SGI-STL

2. 历史文章

•

每日一题：堆排序中建堆过程的时间复杂度

•

吃土记：之前理解时间复杂度计算方式是错误的

•

建堆时间复杂度是o(n)

•

堆排序中建堆过程时间复杂度O(n)怎么来的？