算法魅力之牛叉的前缀和
算法魅力之牛叉的前缀和
禁默
发布于 2025-12-20 18:56:32
发布于 2025-12-20 18:56:32
1.什么是前缀和
前缀和算法(Prefix Sum Algorithm) 是一种常用的算法技巧,用于快速计算数组的某些子数组的和。它通过提前计算出数组中元素的累加和,来加速后续的区间和查询,特别适用于需要频繁查询子数组和的场景。
前缀和的基本思想
给定一个数组 A,前缀和数组 S 是通过将 A 中的每个元素累加得到的数组,具体来说,S[i] 存储的是 A[0] 到 A[i] 的和。
前缀和数组的定义:
S[i] = A[0] + A[1] + ... + A[i]用前缀和数组来求区间和: 通过前缀和数组,我们可以非常快速地求出任意区间 [L, R] 的和,公式为:
sum(L, R) = S[R] - S[L-1]其中 S[R] 是从 A[0] 到 A[R] 的累加和,S[L-1] 是从 A[0] 到 A[L-1] 的累加和,所以 S[R] - S[L-1] 就是 A[L] 到 A[R] 的区间和。
具体步骤
- 构建前缀和数组:
- 初始化前缀和数组
S,其中S[0] = A[0]。 - 对于
i > 0,有:S[i] = S[i-1] + A[i]。
- 初始化前缀和数组
- 查询区间和:
- 对于任意区间
[L, R],通过公式sum(L, R) = S[R] - S[L-1]计算区间和。
- 对于任意区间
优点
- 查询效率高:使用前缀和数组,区间和查询的时间复杂度为 O(1),即常数时间。这使得处理大量区间和查询时非常高效。
- 预处理时间:构建前缀和数组的时间复杂度为 O(n),其中
n是数组的长度。
缺点
- 空间复杂度:需要额外的空间来存储前缀和数组,空间复杂度为 O(n)。
- 适用场景:前缀和算法主要适用于静态数组或不经常更新的数组。如果数组频繁更新,前缀和算法的效率将受到影响,因为每次更新可能需要重新计算前缀和数组。
基本应用场景
- 区间和查询:当你需要频繁查询一个数组的区间和时,前缀和算法是一个非常高效的解决方案。
- 区间最小值/最大值查询:虽然前缀和主要用于求和,但其思想也可以扩展到其他的区间查询问题,如查询区间的最大值或最小值。
- 二维数组问题:前缀和不仅适用于一维数组,也可以扩展到二维数组(矩阵),用于快速计算矩阵中任意子矩阵的和。
2.前缀和练习
2.1 一维前缀和(模版)

287724f941b141569c05b47a2b5a9e52.png
示例:
输入:
3 2
1 2 4
1 2
2 3输出:
3
6这个题就是典型的求区间和
代码展示+算法思路
注意:题目l是大于等于1的,所以我们输入的数组是从1开始输入。
#include <iostream>
using namespace std;
#include <vector>
int main() {
int n,q;
cin>>n>>q;
vector<int> arr(n+1);
for(int i=1;i<=n;i++)
cin>>arr[i];
vector<long long> sum(n+1);
for(int i=1;i<=n;i++)
sum[i]=sum[i-1]+arr[i];
for(int j=0;j<q;j++){
int l=0,r=0;
cin>>l>>r;
cout<<sum[r]-sum[l-1]<<endl;
}
return 0;
}sum 数组是前缀和数组,sum[i] 存储的是从 arr[1] 到 arr[i] 的元素之和。
- 初始时,
sum中的元素被设置为0 - 然后通过循环逐个计算前缀和:
sum[i] = sum[i - 1] + arr[i],也就是每个位置的前缀和是前一个位置的前缀和加上当前元素。
区间查询:对于每个查询 [l, r],通过前缀和公式 sum[r] - sum[l-1] 来求得区间和。这样,单次查询的时间复杂度为 O(1)。
总时间复杂度: O(n + q),其中 n 是数组的大小, q 是查询的数量。
2.2 二维前缀和典型模版

4f5a3041a43c4a74801dfd1f652b4c61.png
算法思路分析
类比于一维数组的形式,如果我们能处理出来从 [0, 0] 位置到 [i, j] 位置这片区域内所有
元素的累加和,就可以在 O(1) 的时间内,搞定矩阵内任意区域内所有元素的累加和。因此我们
接下来仅需完成两步即可:
第一步:搞出来前缀和矩阵
这里就要用到一维数组里面的拓展知识,我们要在矩阵的最上面和最左边添加上一行和一列
0,这样我们就可以省去非常多的边界条件的处理。也可以满足从题目中(1,1)开始。处理后的矩阵就像这样:
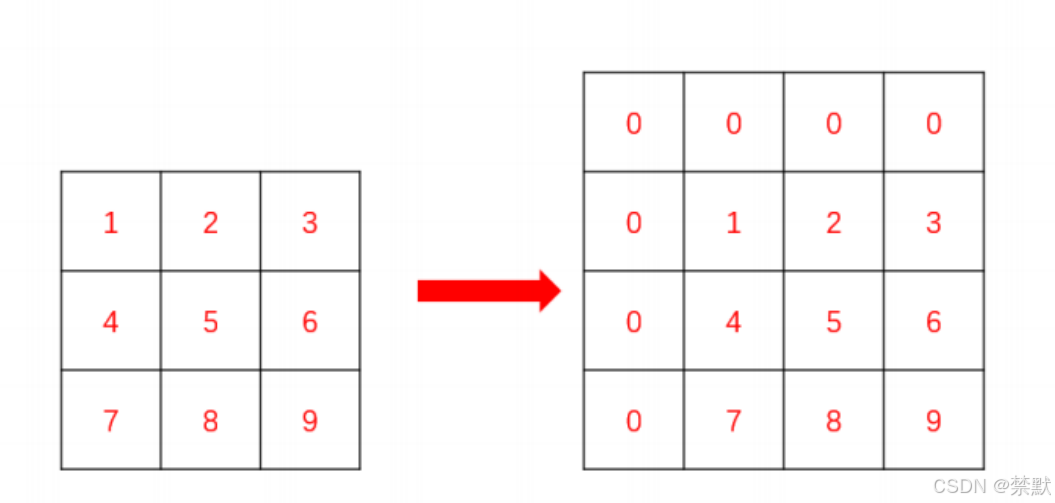
e44be8e76b804ceb90ebf7b16d1b940a.png
填写前缀和矩阵数组的时候,下标直接从 1 开始,能大胆使用 i - 1 , j - 1 位置的值。 注意 dp 表与原数组 matrix 内的元素的映射关系: i. 从 dp 表到 matrix 矩阵,横纵坐标减一; ii. 从 matrix 矩阵到 dp 表,横纵坐标加一。
前缀和矩阵中 dp[i][j] 的含义,以及如何递推二维前缀和方程
dp[i][j] 的含义:
dp[i][j] 表示,从 [0, 0] 位置到 [i, j] 位置这段区域内,所有元素的累加和。对应
下图的红色区域:

cf488af38d804bb4b56bfd8ef979f835.png

969ff7910f5a41f49163c9dcfb68d939.png
使用前缀和矩阵
[x1,y1]----[x2,y2]的和
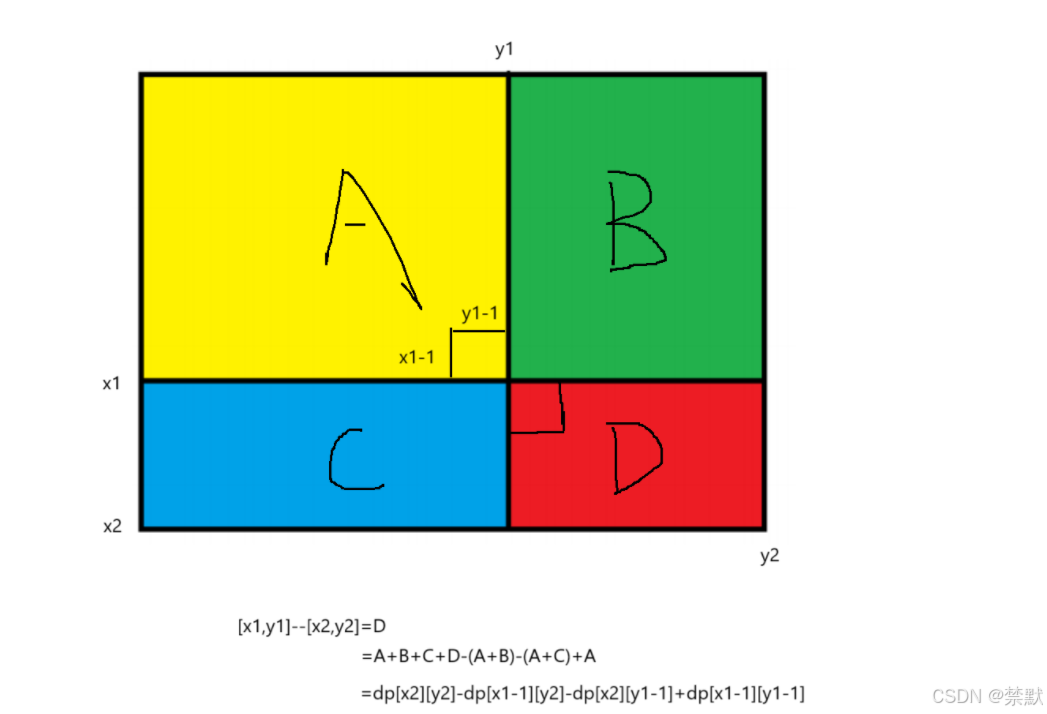
65f359e2dc5142ddb34f3d206d3894da.png
代码展示
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n,m,q;
int arr[1010][1010];
long long dp[1010][1010];
cin>>n>>m>>q;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
cin>>arr[i][j];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1];
}
int x1,y1,x2,y2;
while(q--){
cin>>x1>>y1>>x2>>y2;
cout<<dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1]<<endl;
}
}还是采用的c语言形式定义二维数组比较简便,因为题目给出了行列的数据范围,所以我们直接定义1010为数组行列的个数,初始化都为0 ,不影响加的结果,当然后续遍历也不会用到多余的0数据。
2.3 寻找数组的中心下标

1549fd3cb45c48769927a7984a41b22e.png
通过读取题意就是求i前后区间的和判断是否相等,返回i即可。
因此,我们可以 先预处理出来两个数组,一个表示前缀和,另一个表示后缀和。
然后,我们可以用一个 for 循环枚举可能的中心下标,判断每一个位置的「前缀和」以及 「后缀和」,如果二者相等,就返回当前下标。

9607802395414bf5a9dfb5c45edd9037.png
class Solution {
public:
int pivotIndex(vector<int>& nums) {
int n=nums.size();
vector<int> v1(n),v2(n);
for(int i=1;i<n;i++)
v1[i]=v1[i-1]+nums[i-1];
for(int i=n-2;i>=0;i--)
v2[i]=v2[i+1]+nums[i+1];
for(int i=0;i<n;i++){
if(v1[i]==v2[i])
return i;
}
return -1;
}
};v1[i] 表示:[0, i - 1] 区间所有元和
v2[i] 表示:[i + 1, n - 1] 区间所有元素的和
2.4 除自身以外数组的乘积
238. 除自身以外数组的乘积 - 力扣(LeetCode)

62f450c0154242df818df027c50cf143.png
注意题目的要求,不能使用除法,并且要在 O(N) 的时间复杂度内完成该题。那么我们就不能使
用暴力的解法,以及求出整个数组的乘积,然后除以单个元素的方法。
继续分析,根据题意,对于每一个位置的最终结果 ret[i] ,它是由两部分组成的:
i. nums[0] * nums[1] * nums[2] * ... * nums[i - 1]
ii. nums[i + 1] * nums[i + 2] * ... * nums[n - 1]
于是,我们可以利用前缀和的思想,使用两组 v1和 v2,分别处理出来两个信息:.
v1 表示:i 位置之前的所有元素,即 [0, i - 1] 区间内所有元素的前缀乘积,
v2表示: i 位置之后的所有元素,即 [i + 1, n - 1] 区间内所有元素的后缀乘积
然后再处理最终结果。

e42f3c3f19be4659bc589fc7d9433f28.png
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
vector<int >v;
int n=nums.size();
vector<int>v1(n,1);
vector<int>v2(n,1);
for(int i=1;i<n;i++)
v1[i]=v1[i-1]*nums[i-1];
for(int i=n-2;i>=0;i--)
v2[i]=v2[i+1]*nums[i+1];
for(int i=0;i<n;i++)
v.push_back(v1[i]*v2[i]);
return v;
}
};本题其实和上一道题思路很相似,将前后前缀和换成了前后前缀积
2.5 和为K的子数组

7f6d0bb34441420f83c7820211343627.png
暴力枚举i区间内所有的子数组
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int count = 0;
for (int start = 0; start < nums.size(); ++start) {
int sum = 0;
for (int end = start; end >= 0; --end) {
sum += nums[end];
if (sum == k) {
count++;
}
}
}
return count;
}
};但是会重复计算很多次相同数字的和 ,简单优化求出所有前缀和存放在数组中,在暴力枚举所有区间,统计等于k的个数。
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int n=nums.size();
vector<int>v(n+1);
for(int i=1;i<=n;i++){
v[i]=v[i-1]+nums[i-1];
}
int count=0;
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++)
if(v[i]-v[j]==k)
count++;
}
return count;
}
};哈希+前缀和,将前缀和存在哈希表中。
设 i 为数组中的任意位置,用 sum[i] 表⽰ [0, i] 区间内所有元素的和。
想知道有多少个「以 i 为结尾的和为 k 的子数组」,就要找到有多少个起始位置为 x1, x2,
x3... 使得 [x, i] 区间内的所有元素的和为 k 。那么 [0, x] 区间内的和就是sum[i] - k 了。于是问题就变成:
找到在 [0, i - 1] 区间内,有多少前缀和等于 sum[i] - k 的即可。
不用真的初始化一个前缀和数组,因为只关⼼在 i 位置之前,有多少个前缀和等于
sum[i] - k 。因此,我们仅需用一个哈希表,一边求当前位置的前缀和,一边存下之前每一种
前缀和出现的次数。
当我们的整个数组和=k时,则sum-k=0 则我们先定义一个hash[0]=1,因为不存在【0,-1】这个区间。
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
unordered_map<int,int> hash;
hash[0]=1;
int sum=0;
int ret=0;
for(auto e: nums ){
sum+=e;
if(hash.count(sum-k))
ret+=hash[sum-k];
hash[sum]++;
}
return ret;
}
};结束语
本节内容就到此结束了,前缀和的题目还有很多,后续有时间也会继续更新前缀和的相关题目分享,也欢迎友友一起讨论。 最后,感谢各位友友的支持!!!
本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2024-11-29,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录

