C++ string 高频算法题精选：从反转、回文到数字转换

前言

大家好啊，我是云泽Q，欢迎阅读我的文章，一名热爱计算机技术的在校大学生，喜欢在课余时间做一些计算机技术的总结性文章，希望我的文章能为你解答困惑~

一、string相关OJ题

1.1 仅仅反转字母（swap）

仅仅反转字母

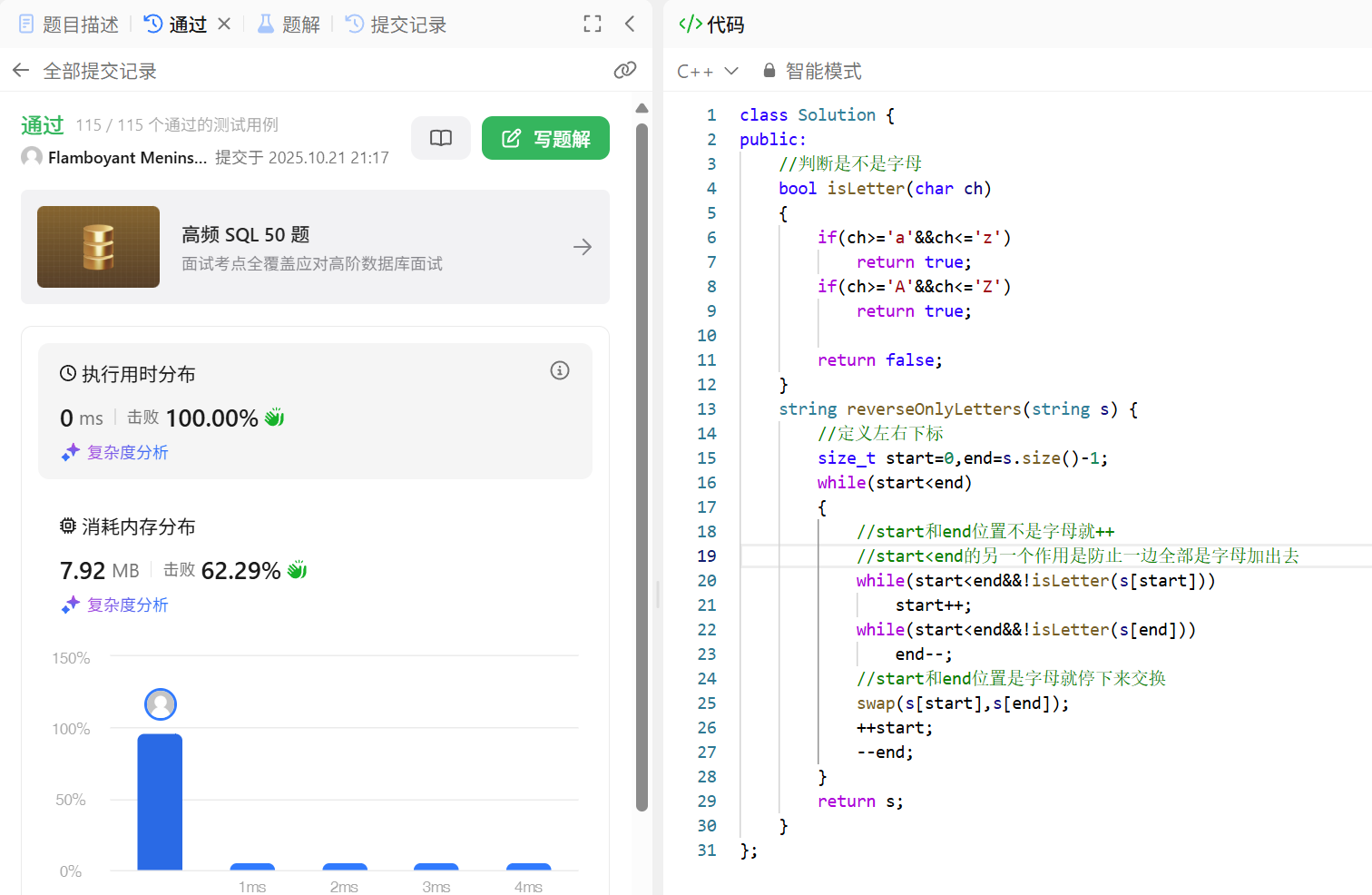
该题目的思路就是找到字符串左右两边的字母进行交换即可，和快排的思路很像

在这里插入图片描述

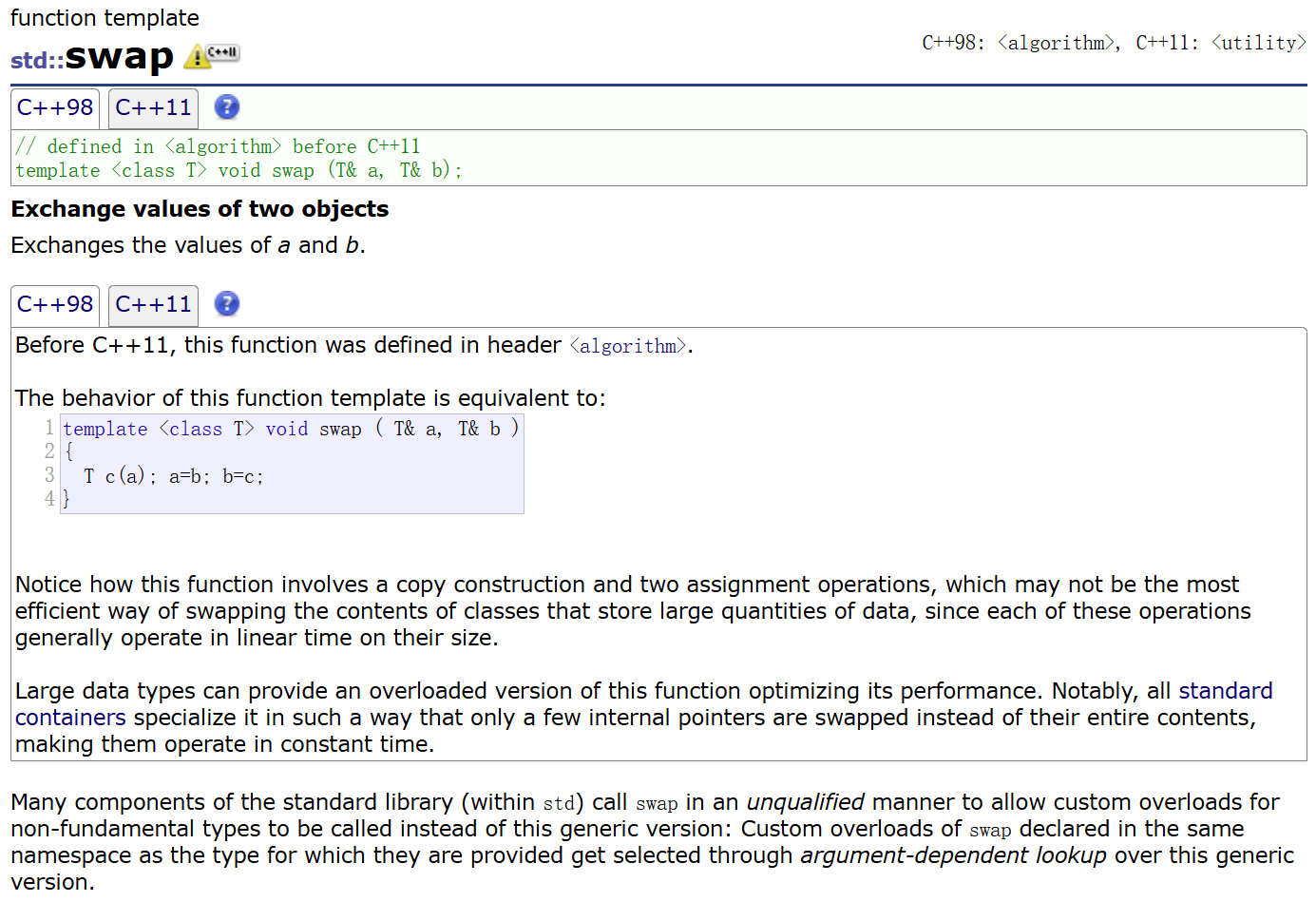
C++的交换也不用自己写，直接用库里面实现的函数模板就好，任何类型都可以交换

在这里插入图片描述

1.2 字符串中的第一个唯一字符

字符串中的第一个唯一字符

在这里插入图片描述

最简单的思路就是拿每个字符和其他字符比对一遍，补充：下标也叫索引 这种方式很暴力很挫，如果有n个字符时间复杂度就是n方，在算法竞赛中肯定是不行的，直接说下一个思路

在这里插入图片描述

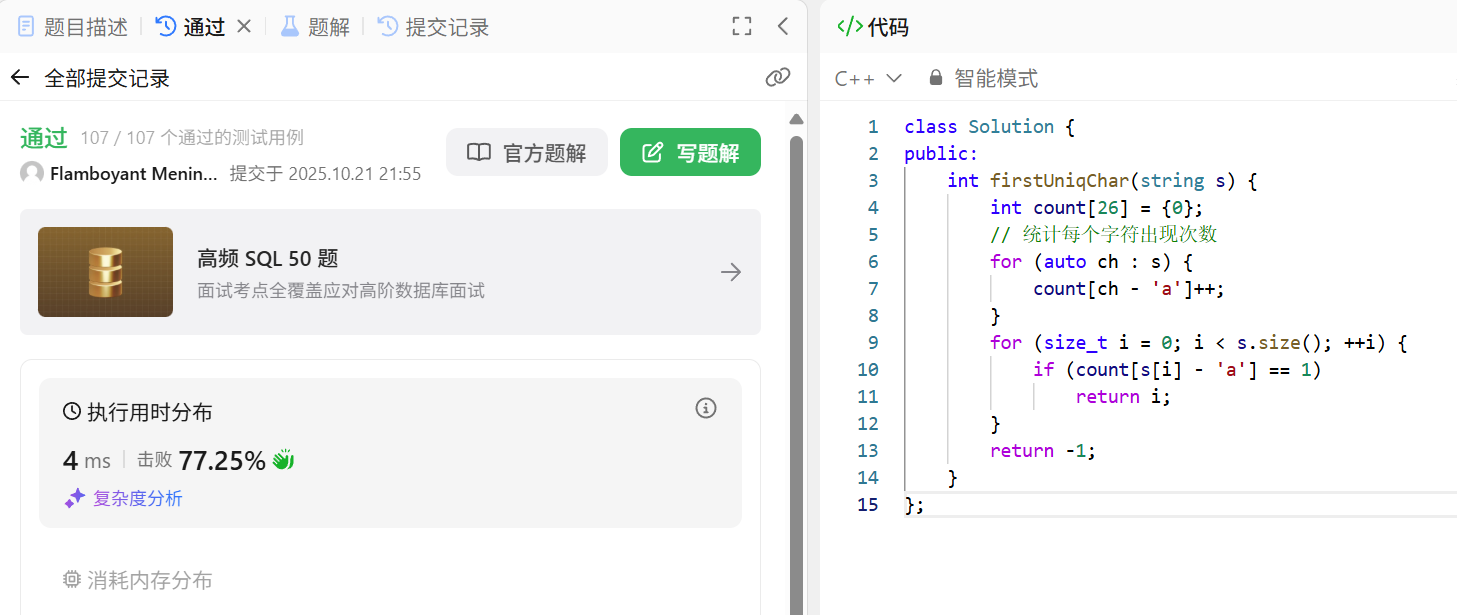
该思路叫计数排序，本质上是一种哈希

1. 统计字符出现次数 由于字符串仅包含小写字母（共 26 个），因此可以用一个长度为 26 的数组 count 来统计每个字符的出现次数。 对于字符串中的每个字符 ch，通过 ch - ‘a’ 将其映射为数组的索引（例如 若ch字符为a，a-a=0，虽然写的是字符a，但是计算的时候会取其ASCII码计算，ch是b，结果为1，ch为c，结果为2。‘a’ 对应索引 0，‘b’ 对应索引 1，以此类推）。 遍历字符串时，对每个字符的对应索引执行 count[ch-‘a’]++，最终数组的每个元素就代表了对应字母的出现次数。
2. 查找第一个唯一字符 再次遍历字符串，对每个字符 s[i]，检查其在 count 数组中对应的计数值： 若 count[s[i]-‘a’] == 1，说明该字符是第一次出现且仅出现一次，直接返回其索引 i。 若遍历完整个字符串都没有找到这样的字符，返回 -1。

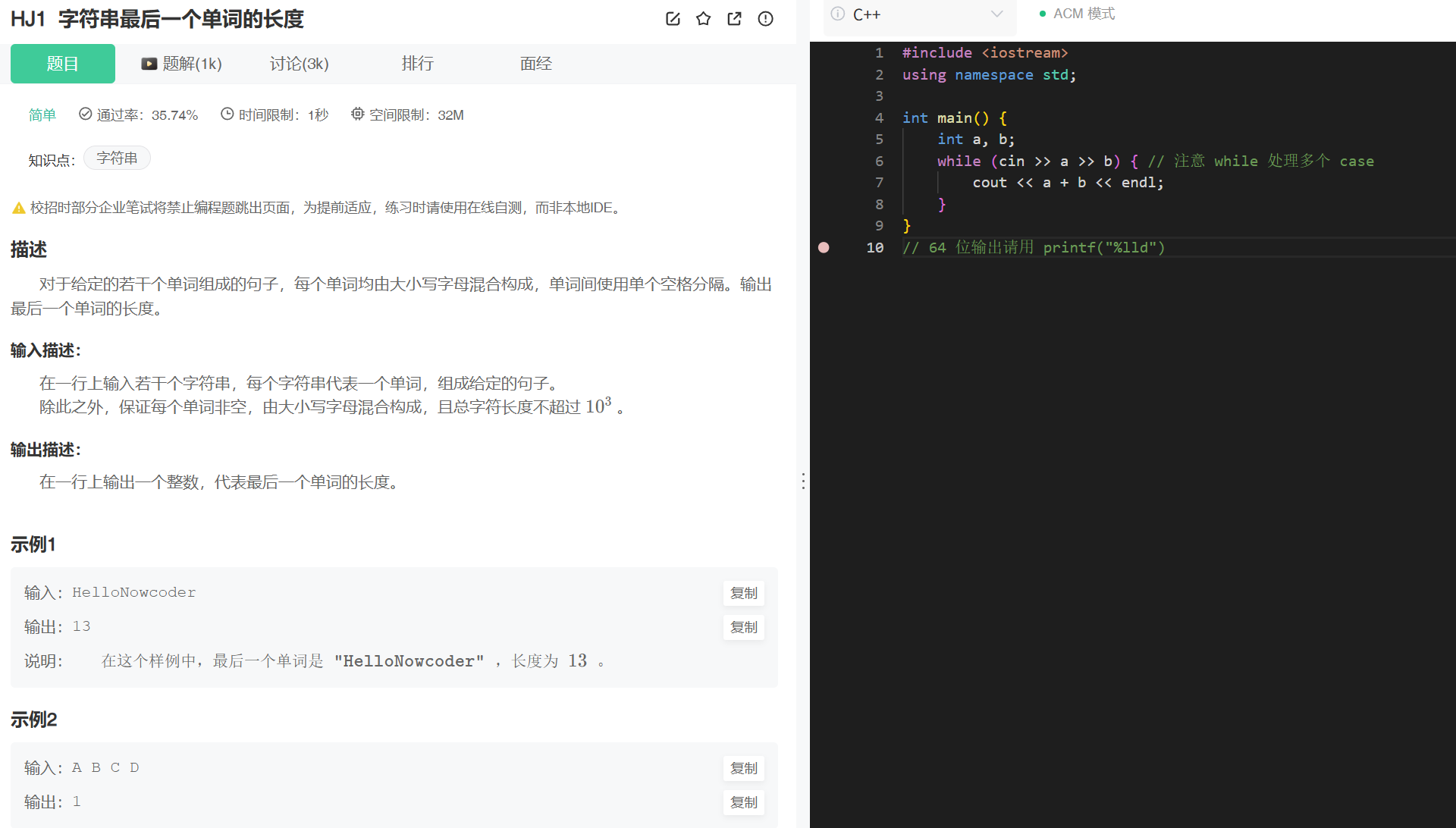
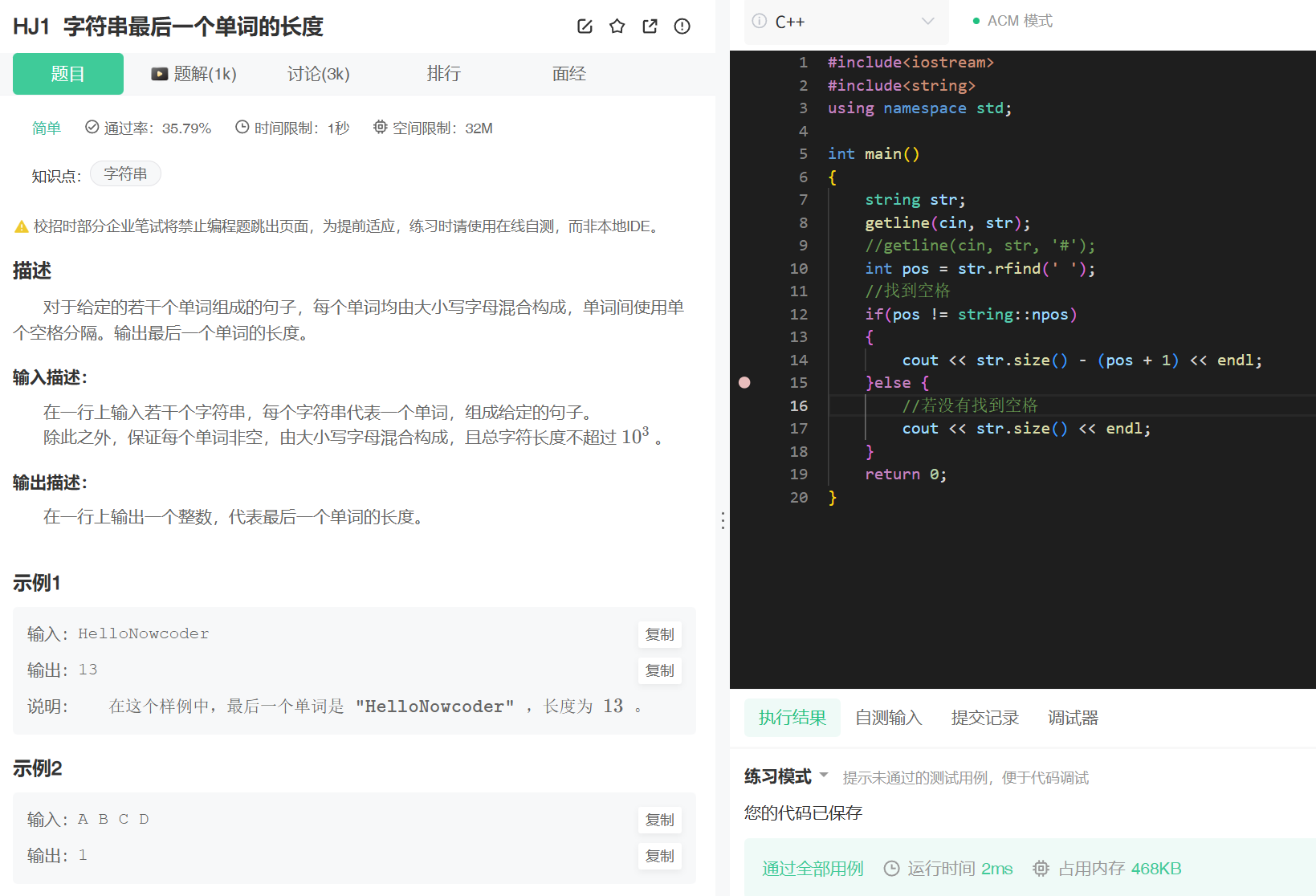
1.3 字符串最后一个单词的长度（rfind，getline）

字符串最后一个单词的长度

在这里插入图片描述

该题的本质还是找空格，比如说一个字符串hello world可以使用之前的find找空格，但是一个字符串有多个空格就不好确定哪个空格之后是最后一个单词了，这时候就需要倒着找了，这个功能库中也有接口实现

在这里插入图片描述

在这里插入图片描述

rfind就是倒着找，其第二个参数默认给npos。会从最后一个字符往前找，例如从8位置（下标为8）倒着找，第二个参数给8就可以了

string 类的 rfind 函数的返回规则： 如果找到指定字符（这里是空格），返回该字符的最后一个出现位置的索引（索引范围是 0 ~ str.size() - 1）。 如果没找到，返回 string::npos（这是一个特殊的无符号整数，值远大于普通字符串的长度）。

找到最后一个字符之后就要计算字符长度了,长度计算有一个技巧，左闭右开减掉就是个数[0，10)，左闭右闭减了之后+1才是个数[0,9]，

size是开区间位置，pos不是闭区间位置，闭区间位置应该从w开始

在这里插入图片描述

在这里插入图片描述

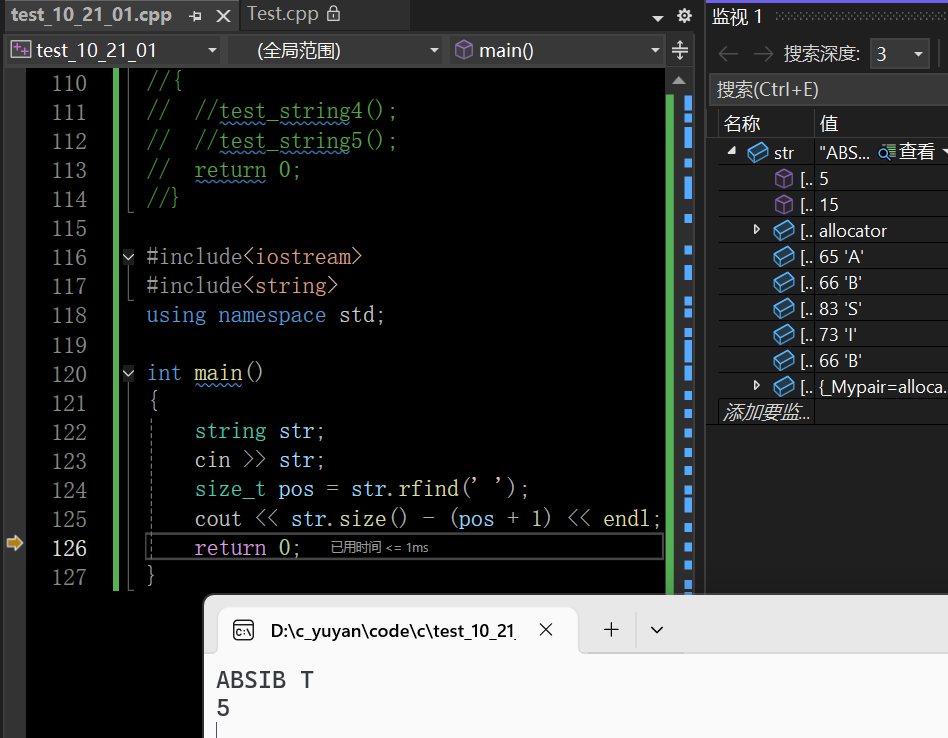
然而运行是不通过的，只通过了3个测试用例

在这里插入图片描述

可以看到最后一个字符和空格没输入进去，没找到空格的话pos就是-1，相当于42亿9千万+1就溢出了，溢出为0，所以输出结果为str.size()，这里是一个巧合

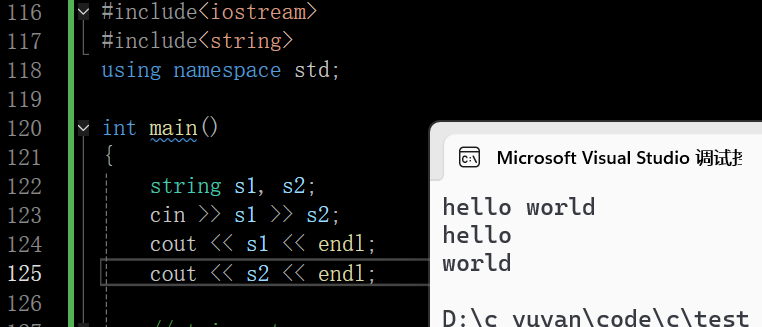
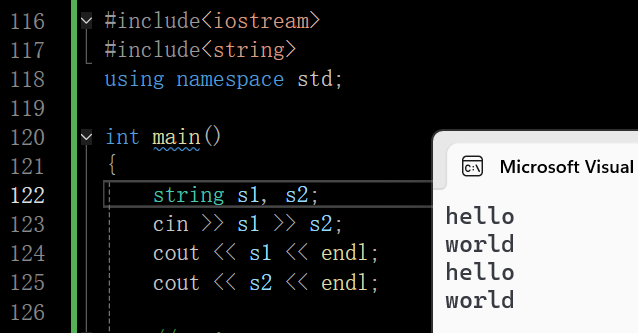
这里流提取没有输入实际的东西是因为C/C++有一个规定，无论是scanf和cin，若输入多个值，规定空格或者换行会作为他们的间隔

在这里插入图片描述

在这里插入图片描述

也就是如果输入一个带空格的字符串，cin是输入不了空格的

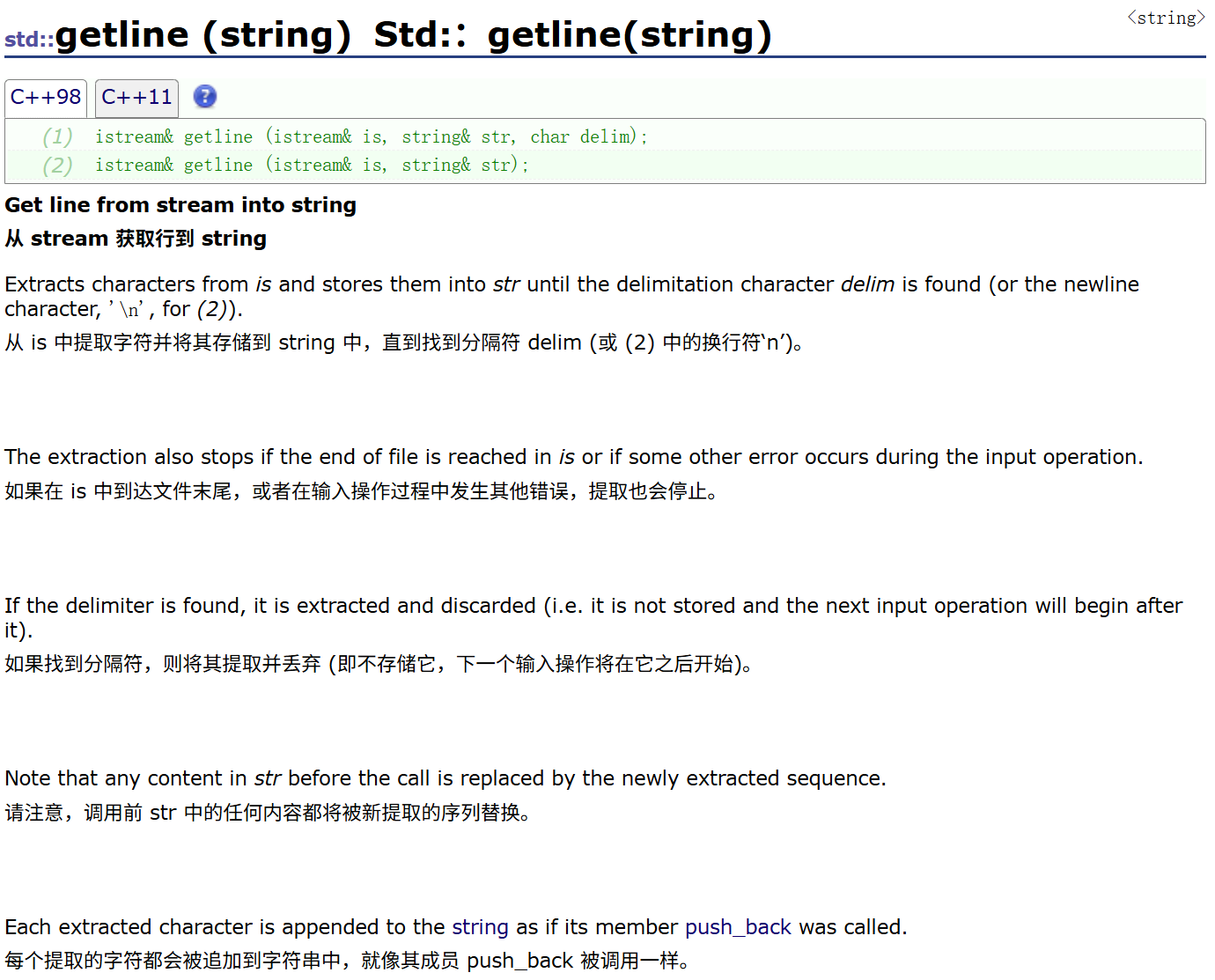
这时候就要使用getline了，C++库中早已考虑到这样的情况

在这里插入图片描述

getline不会用空格作为中止，而是默认以换行作为中止，甚至可以自定义结束符

在这里插入图片描述

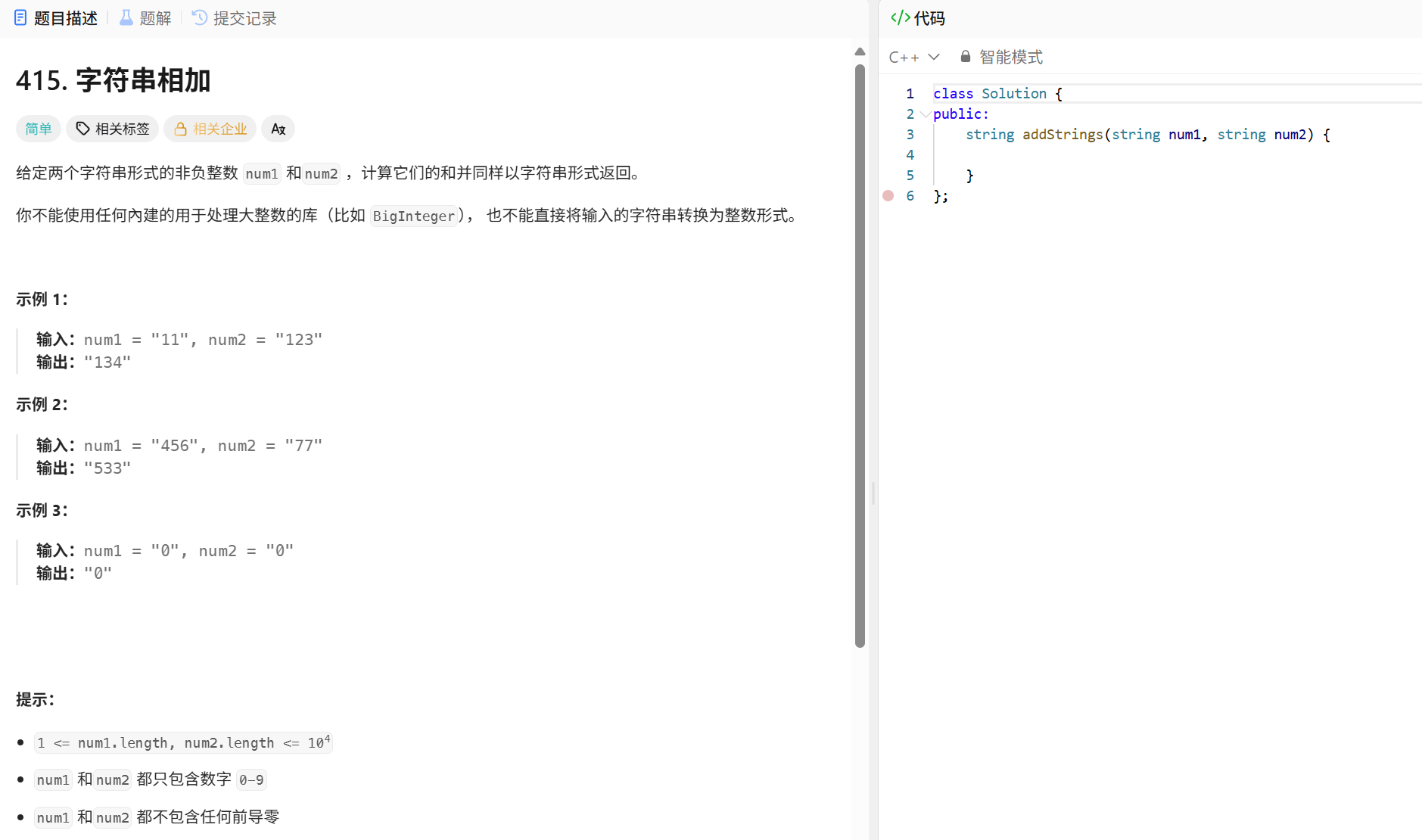
1.4 字符串相加（reverse）

字符串相加

在这里插入图片描述

1. 题目要求 给定两个字符串形式的非负整数 num1 和 num2，计算它们的和并以字符串形式返回。要求： 不能使用处理大整数的内置库（如 BigInteger）； 不能直接将字符串转换为整数（因为字符串长度可能很大，超过整数类型范围）。

在科研的一些领域里，计算机无法对需求直接运算，计算机支持的整型运算就是4个字节或8个字节，4个字节最多能表示的整数就是42亿9千万，两个很大的数相加可能就溢出了，8个字节可以大一些，但是也大不了多少。 要支持这样几十位的整数运算，就需要一个大整数运算库，库里面的整数用字符串来存，就算一个整数一千位，也只需要一千个字节（1KB）来存，用字符串存储大整数就很简单了，运算的由自己来控制

这里有三种情况

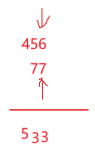
比如字符串456+77，就要倒着访问string，可以用下标也可以用迭代器，我这里用下标，首先字符‘6’+‘7’是二者的ASCII码相加肯定是不对的，要把二者转换为整数相加，从后往前两串的每个字符依次相加，结果533再用字符存起来

在这里插入图片描述

这里最后一位相加没有进位，短的串就结束了，但是也不能把上面剩余的长的串直接拷贝下去，这是因为还有第三种情况

在这里插入图片描述

这种情况就不能直接拷贝了

在这里插入图片描述

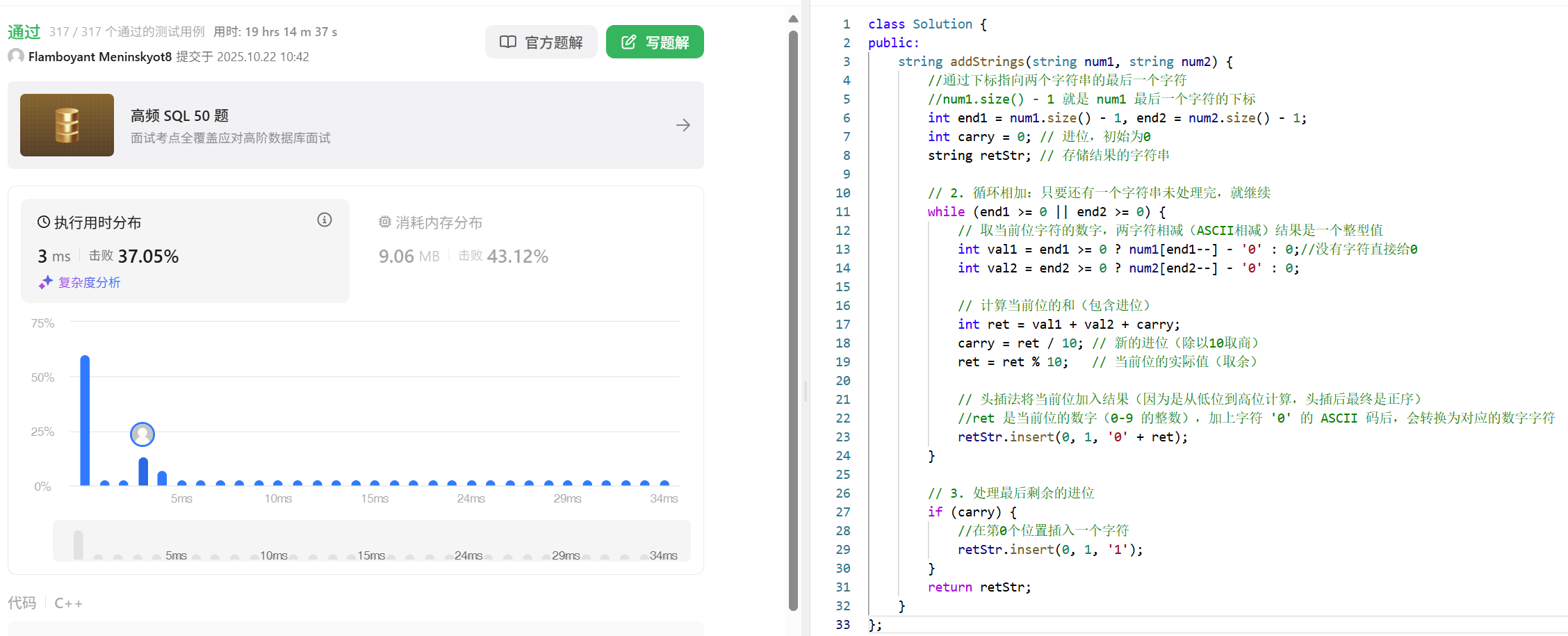
这里最好的解决方式就是短串的结束不能算结束，长串也要加完，有进位的加进位，没进位的加零

在这里插入图片描述

注意，处理最后剩余的进位的代码是为了应对下面的情况： 当num1=“1”，num2=“9”时，ret结果为10，carry位1，ret为0，此时就直接0头插进结果字符串了（此时结果为“0”），正确结果应该为“10”

这道题目还有可以优化的地方，表面看是按最长字符的时间复杂度来算，最多不过O（N），但是头插是个性能杀手 当我们在字符串开头插入字符时（比如在 “abc” 的开头插入 ‘x’），需要先给新字符腾出第一个位置。但原来的第一个字符（‘a’）、第二个字符（‘b’）、第三个字符（‘c’）已经占据了从首地址开始的连续空间，因此必须将它们依次向后挪动一个位置（‘a’ 移到原来 ‘b’ 的位置，‘b’ 移到原来 ‘c’ 的位置，‘c’ 移到新的空闲位置），才能把新字符 ‘x’ 放在最前面。

若字符串的长度为N，第一个头插的数据不用挪，往后每个数据插入，后面的数据都要挪动一次，第二个字符插入后面1个数据挪动一次，第三个字符插入后面两字符挪动1次…若有N个字符，最后一个字符插入，后面有N-1个数据要挪动一次，也就是插入的时候挪动的次数是1+2+…+N-1。若循环走N次，插入N个字符，实现复杂就为O（N2）

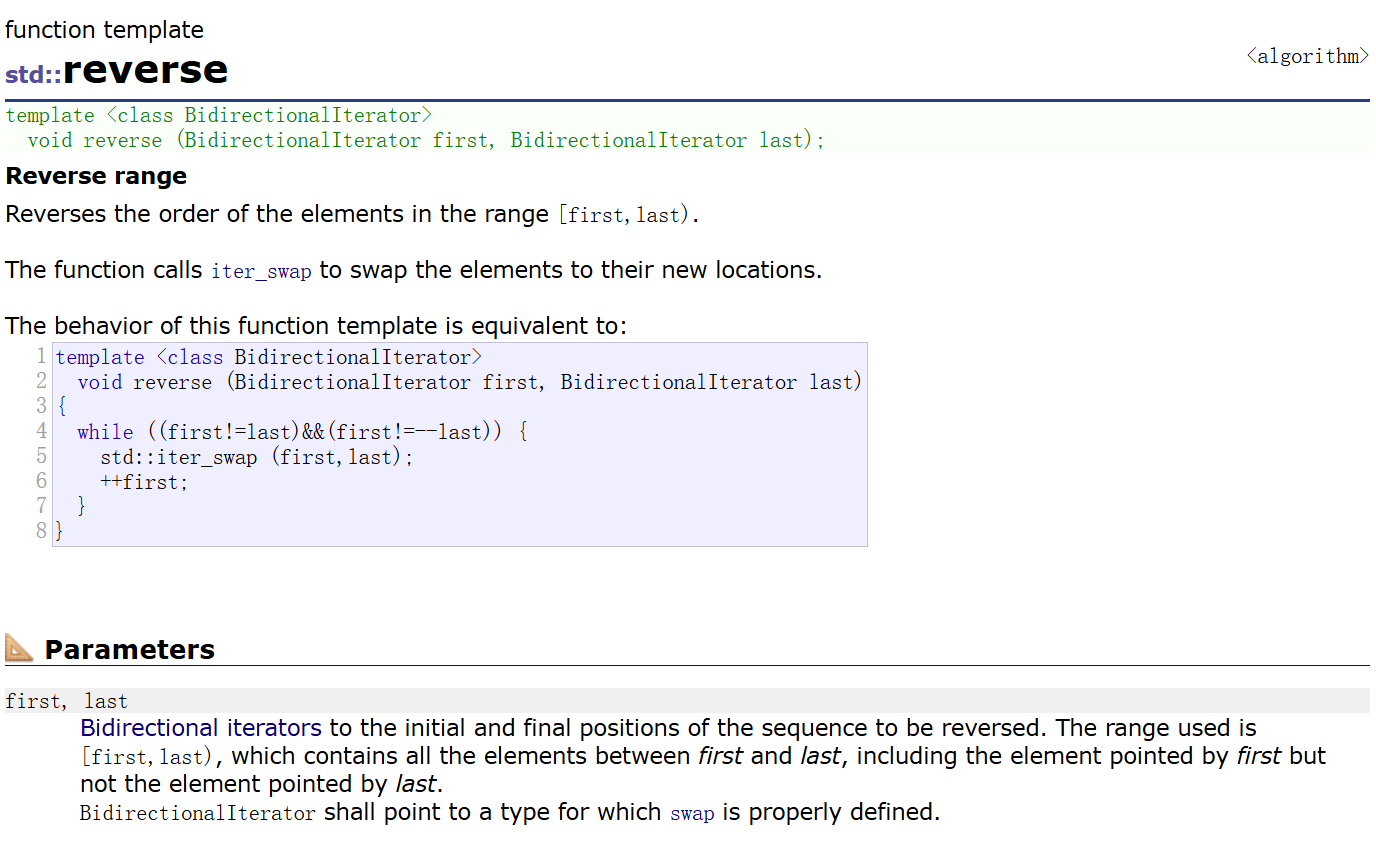
可以将头插改为尾插，只不过尾插之后需要将数据进行逆置（reverse，给一段迭代器区间，就会把迭代器区间中的值进行逆置）

在这里插入图片描述

在这里插入图片描述

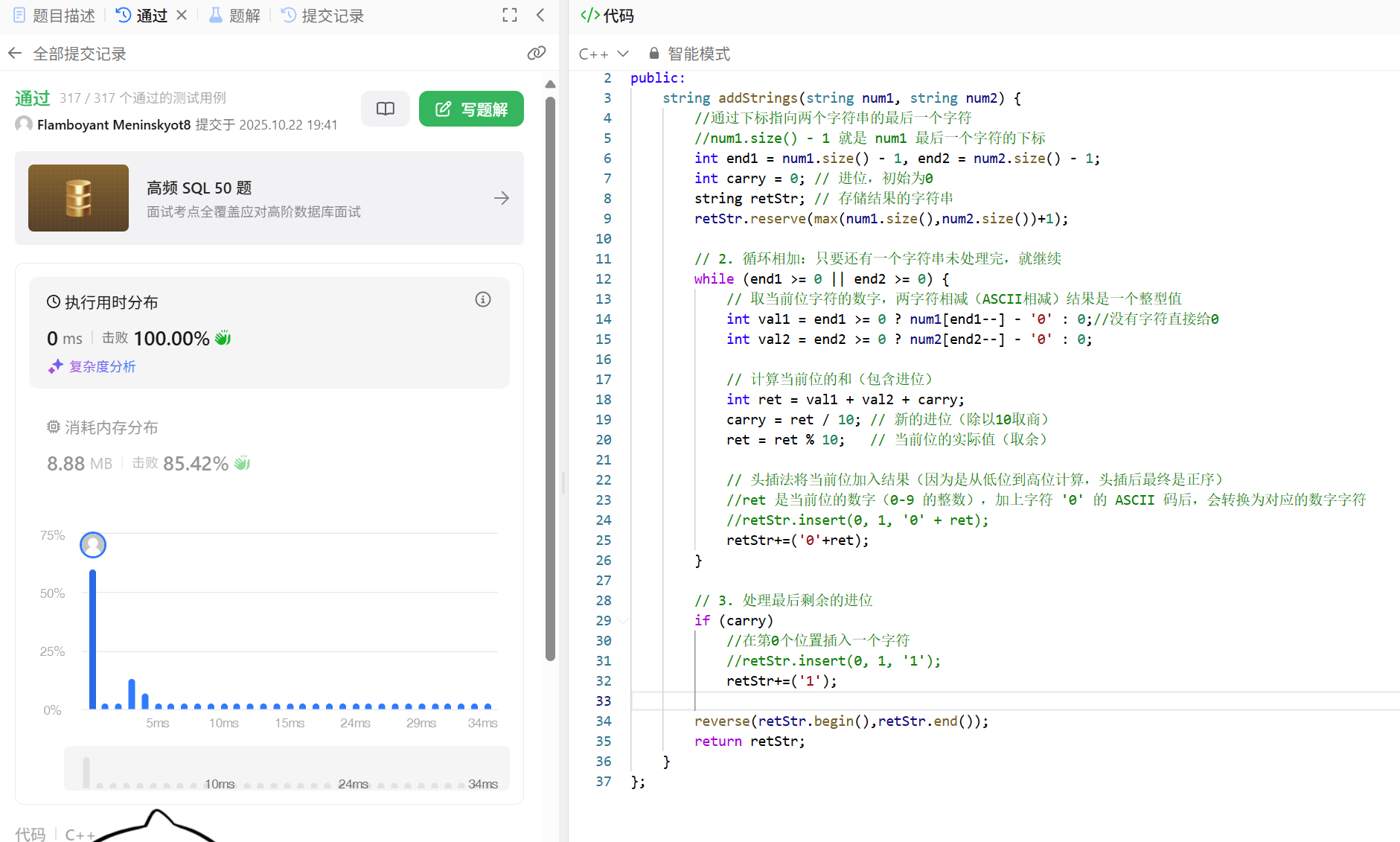
+=就可以替代尾插，这里还有一个优化点就是如果字符串很长，+=就要不断进行扩容，这就可以使用reserve，提前按大的字符串开一个空间（算法库中还有一个叫max的函数），顺便多加一个1，因为可能最后会有一个进位

在这里插入图片描述

这样时间复杂度就为O（N）了

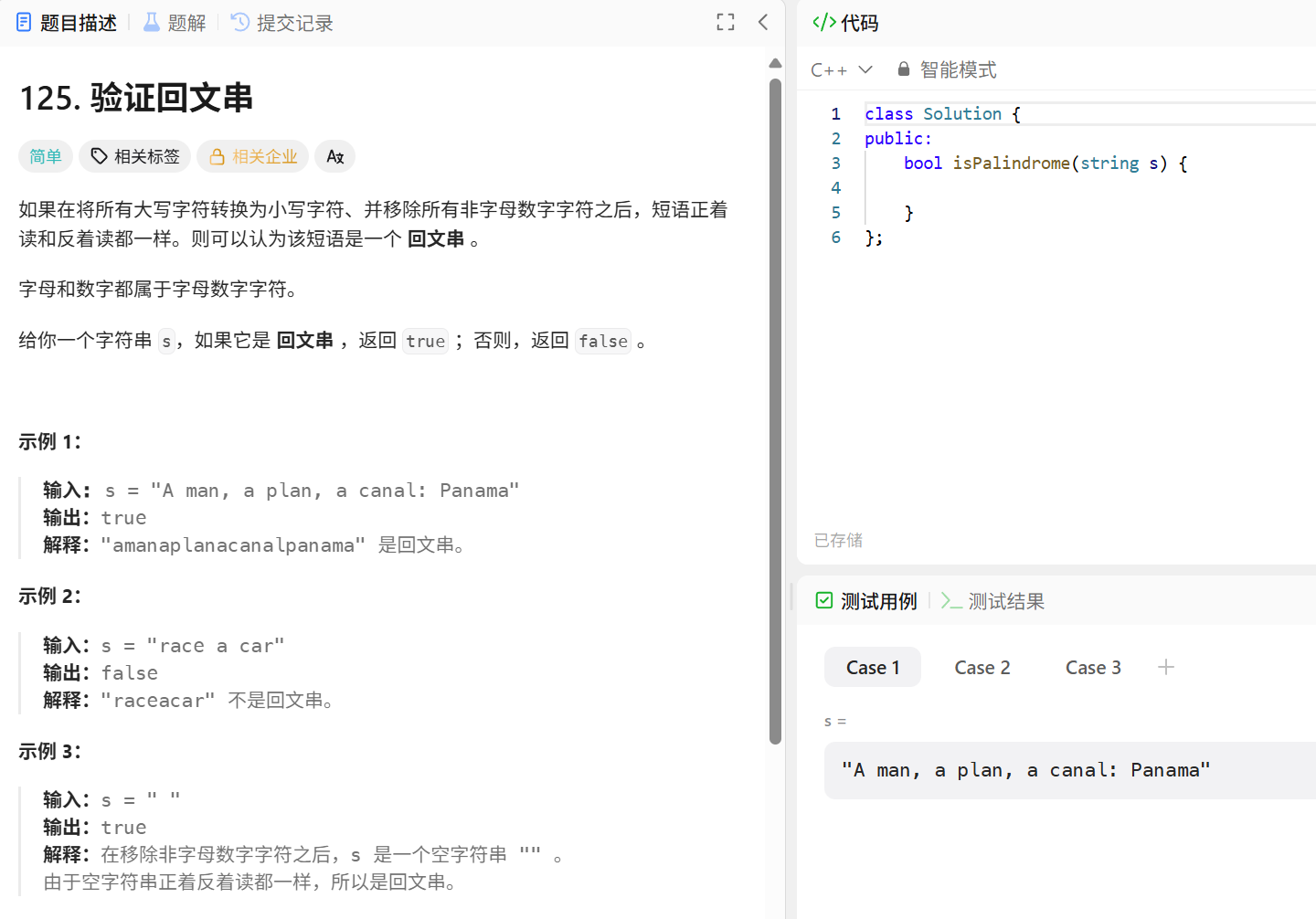
1.5 验证回文串(isalnum,tolower)

验证回文串

在这里插入图片描述

思路：

1. 预处理字符串：将字符串中的非字母数字字符移除，并将所有字符转换为小写。
2. 使用双指针法，一个指针从字符串头部开始，另一个从尾部开始，向中间移动并比较字符是否相同。
3. 如果所有对应的字符都相同，则是回文串；否则不是。

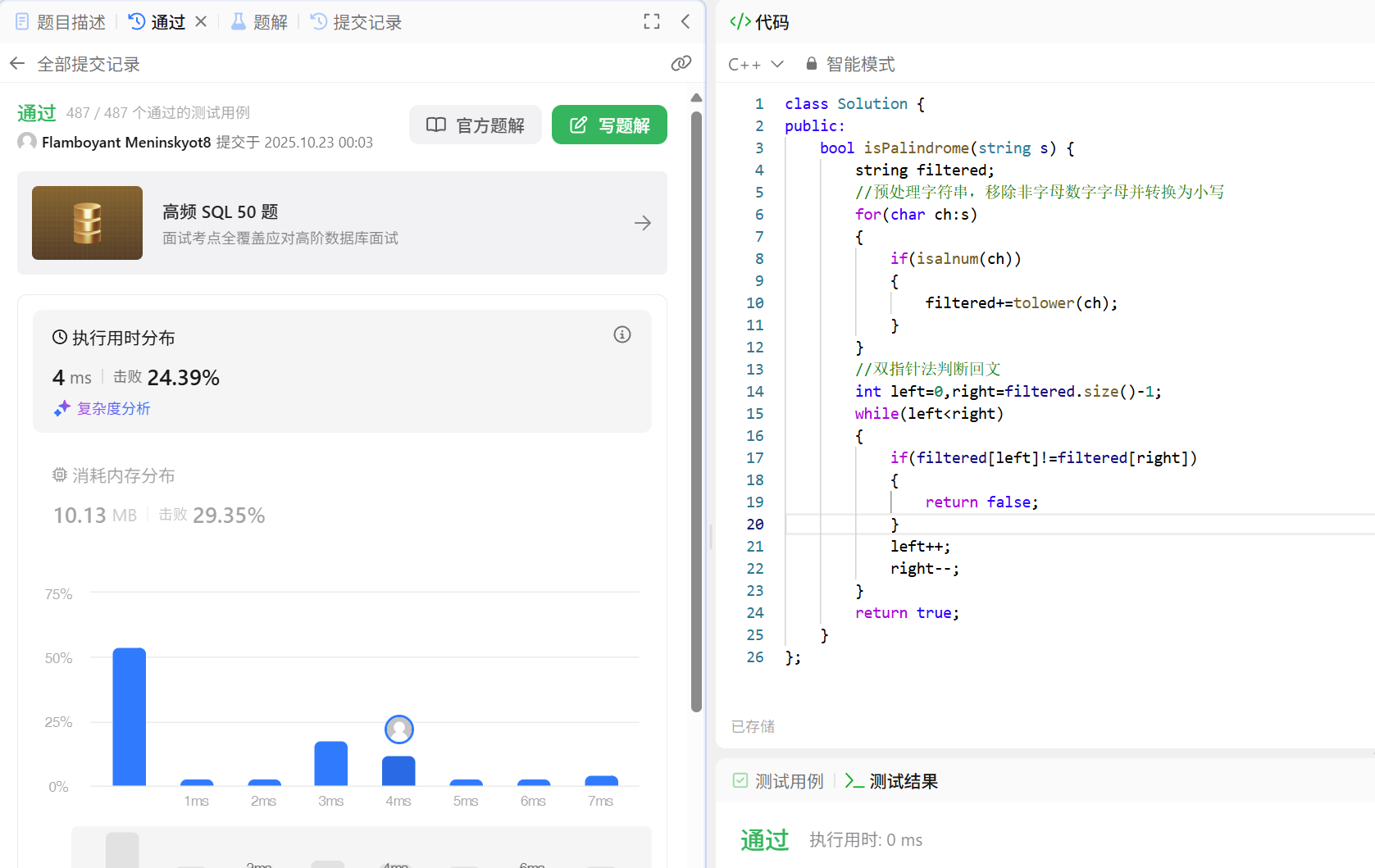
在这里插入图片描述

• 首先遍历原字符串，使用isalnum函数判断字符是否为字母或数字，如果是则通过tolower转换为小写并添加到新字符串中。
• 使用双指针法，左指针从字符串开头向右移动，右指针从字符串末尾向左移动。
• 比较左右指针指向的字符，如果发现不相同的字符立即返回false。
• 如果所有字符比较都相同，则返回true。

isalnum 和 tolower是C 标准库字符处理函数，在 C++ 中被包含在 < cctype > 头文件中（对应 C 语言的 < ctype.h >），用于单个字符的属性判断和转换。

在这里插入图片描述

在这里插入图片描述

注意：当使用 left != right 作为循环条件时，可能会遇到以下问题： 4. 偶数长度字符串的问题 对于偶数长度的字符串，当 left 和 right 相遇时，实际上已经比较完成，但 left != right 仍然为 true，会导致继续循环：

示例：字符串 "abba"（长度为4）
- 初始：left=0, right=3
- 第一轮比较后：left=1, right=2
- 第二轮比较后：left=2, right=1  ← 此时 left > right，但 left != right 仍为 true
- 继续循环：出现越界访问风险

1.6 把字符串转换成整数

把字符串转换成整数

在这里插入图片描述

在这里插入图片描述

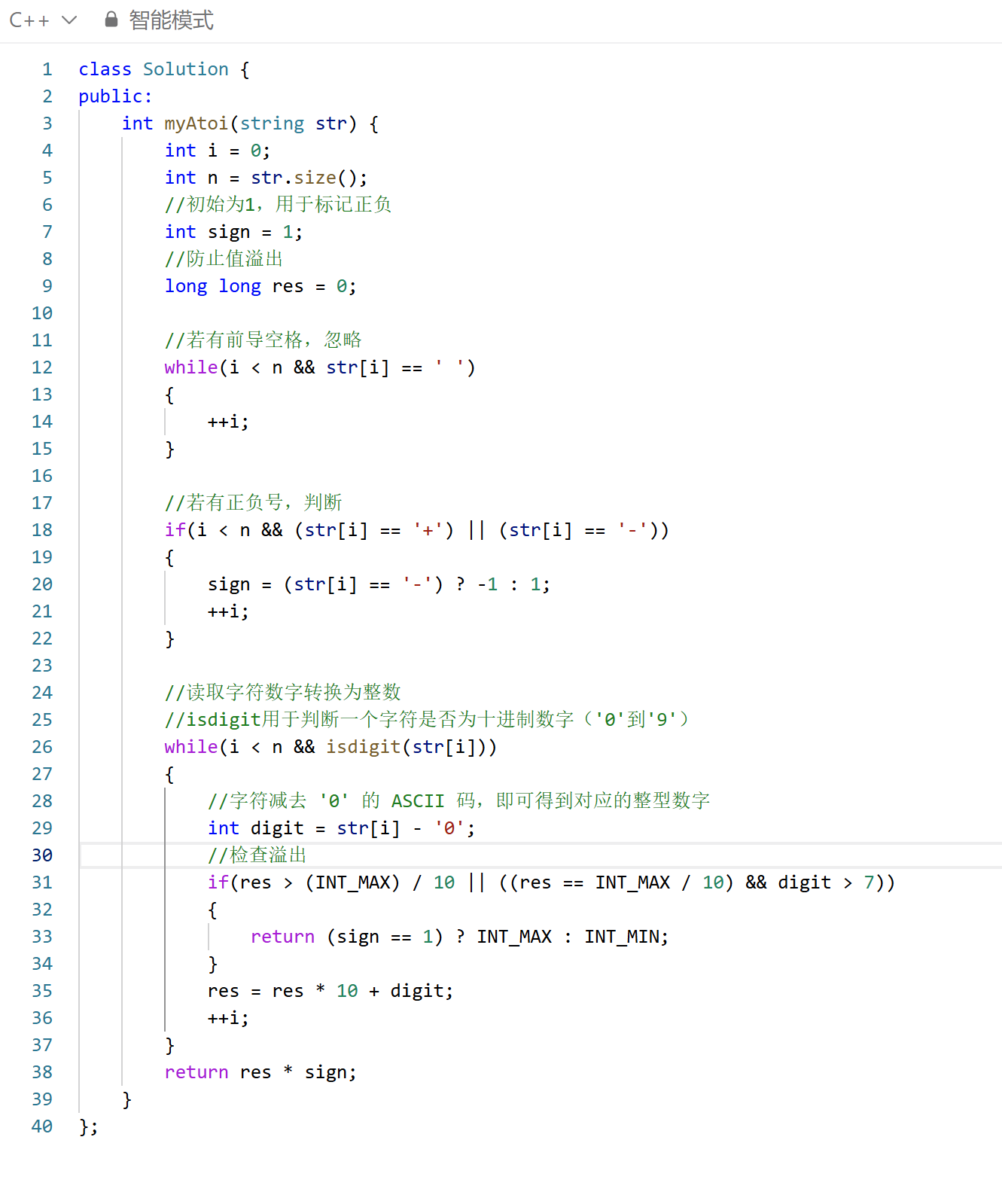
解题思路：

1. 处理前导空格：首先跳过字符串开头的所有空格。
2. 判断符号：识别字符串的正负号，默认是正数。
3. 读取数字：连续读取数字字符，转换为整数。
4. 处理溢出：若转换后的整数超出 32 位有符号整数范围（[-2^31, 2^31 - 1]），则截断为边界值。

在这里插入图片描述

32 位有符号整数的范围是 [-231, 231 - 1]（即[-2147483648, 2147483647]） INT_MAX：32 位有符号整数的最大值 231 - 1 = 2147483647 INT_MIN：32 位有符号整数的最小值 -231 = -2147483648

在这里插入图片描述

1.7 反转字符串

反转字符串

在这里插入图片描述

思路分析：

• 定义两个指针：left 从字符串头部（索引0）开始，right 从字符串尾部（索引s.size() - 1）开始。
• 循环交换 left 和 right 指向的字符，然后将 left 右移、right 左移，直到 left >= right（此时所有字符已交换完成）。

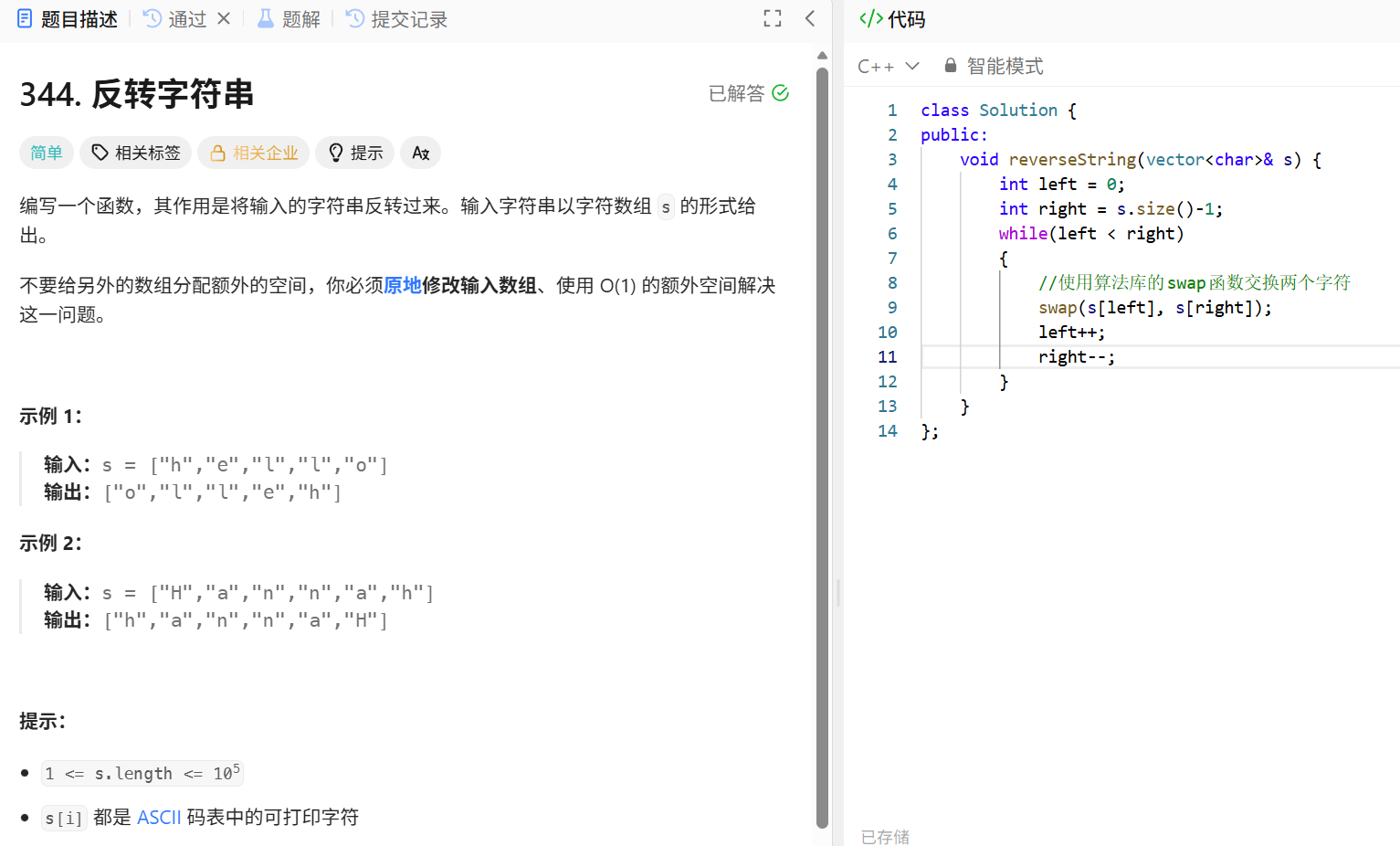
在这里插入图片描述

补充：该题目既可以手动实现交换，也可以直接使用Swap函数

1.8 字符串相乘

字符串相乘

在这里插入图片描述

注意：该题目要注意数值溢出情况，不能将字符串直接转换为整数进行操作，若字符串长度为200，就会超出整数类型的范围，且要特殊处理字符串“0”

核心思想：模拟竖式乘法

    1 2 3
  ×   4 5 6
  ---------
        7 3 8   ← 123 × 6
      6 1 5     ← 123 × 5（向左移一位）
    4 9 2       ← 123 × 4（向左移两位）
  ---------
    5 6 0 8 8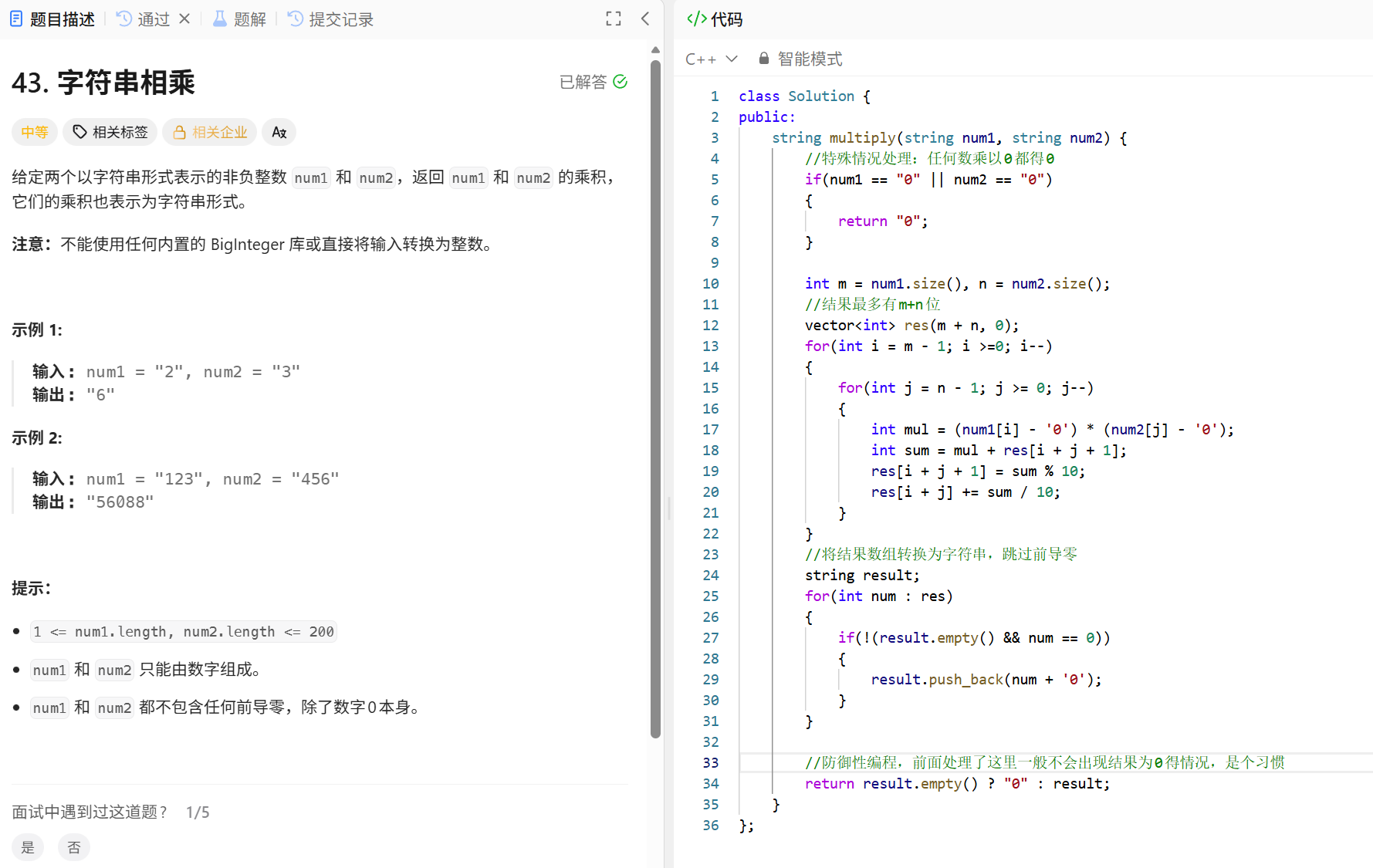

在这里插入图片描述

这里解释一下为什么中间数组的长度是m+n

• 两个数相乘，结果的最大位数是两个数位数之和。比如：999 × 999 = 998001（3位 × 3位 = 6位）

下面说一下该代码最核心的部分：逐位相乘 用 num1 = “123”, num2 = “456” 来详细演示： 数组索引对应关系：

num1: 索引 0->'1', 1->'2', 2->'3'
num2: 索引 0->'4', 1->'5', 2->'6'
res:  索引 0 1 2 3 4 5

第一次循环：i=2 (num1[2]=‘3’), j=2 (num2[2]=‘6’)

计算：3 × 6 = 18
位置：i+j = 2+2 = 4, i+j+1 = 2+2+1 = 5
res[5] = 18 % 10 = 8  （个位）
res[4] += 18 / 10 = 1 （十位）
当前res: [0,0,0,0,1,8]

第二次循环：i=2 (num1[2]=‘3’), j=1 (num2[1]=‘5’)

计算：3 × 5 = 15
位置：i+j = 2+1 = 3, i+j+1 = 2+1+1 = 4
当前res[4] = 1，所以：15 + 1 = 16
res[4] = 16 % 10 = 6
res[3] += 16 / 10 = 1
当前res: [0,0,0,1,6,8]

第三次循环：i=2 (num1[2]=‘3’), j=0 (num2[0]=‘4’)

计算：3 × 4 = 12
位置：i+j = 2+0 = 2, i+j+1 = 2+0+1 = 3
当前res[3] = 1，所以：12 + 1 = 13
res[3] = 13 % 10 = 3
res[2] += 13 / 10 = 1
当前res: [0,0,1,3,6,8]

继续处理 num1[1]=‘2’…，最终所有循环结束后，res数组会是：[0,5,6,0,8,8]

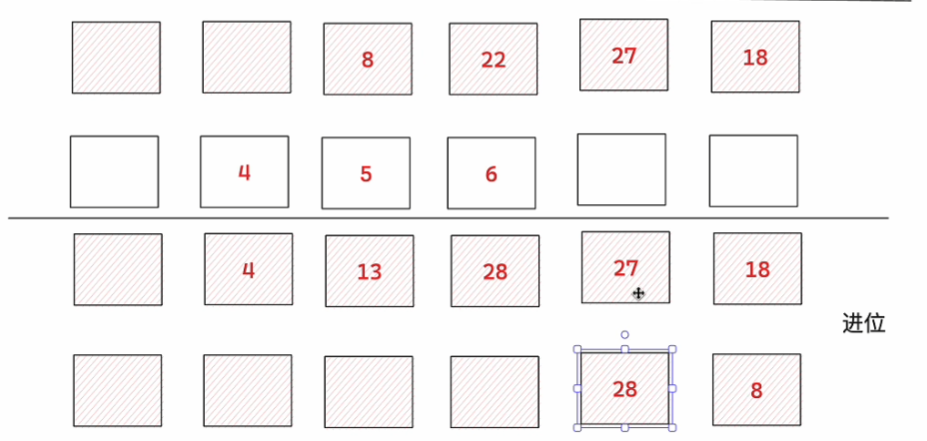
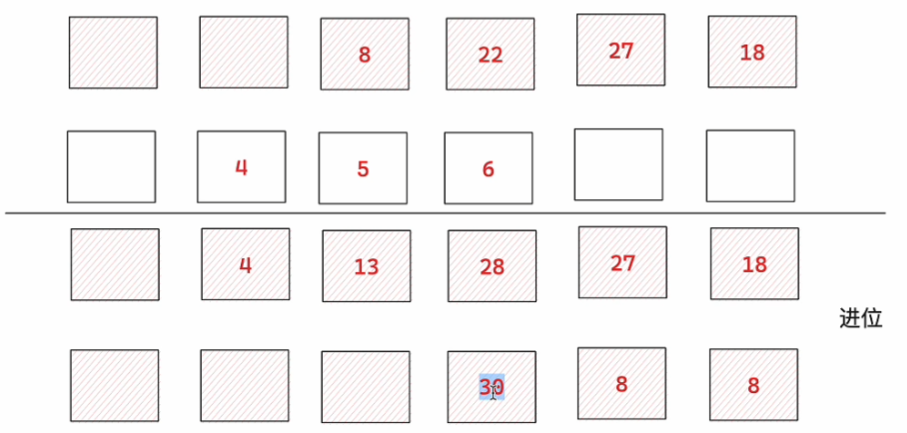
关键理解：num1的第i位与num2的第j位相乘，结果应该放在res[i+j]和res[i+j+1] 这是因为： 在十进制中，第i位实际上代表的是 数字 × 10i 所以 num1[i] × num2[j] 实际上是 (数字1 × 10i) × (数字2 × 10j) = 结果 × 10(i+j) 因此这个乘积会影响结果的第i+j位和第i+j+1位

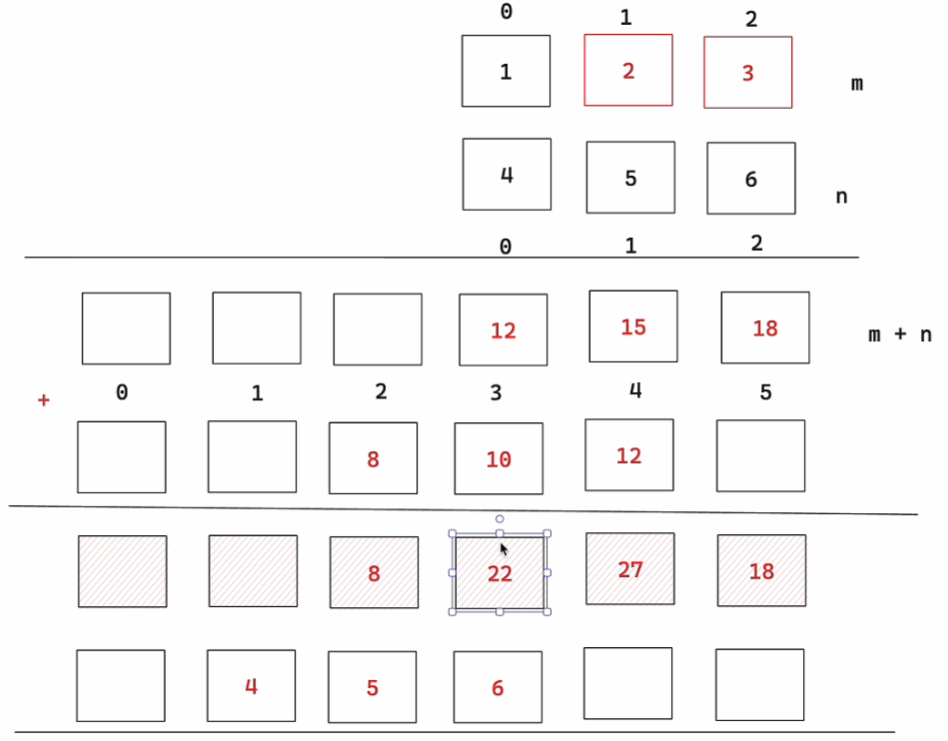
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

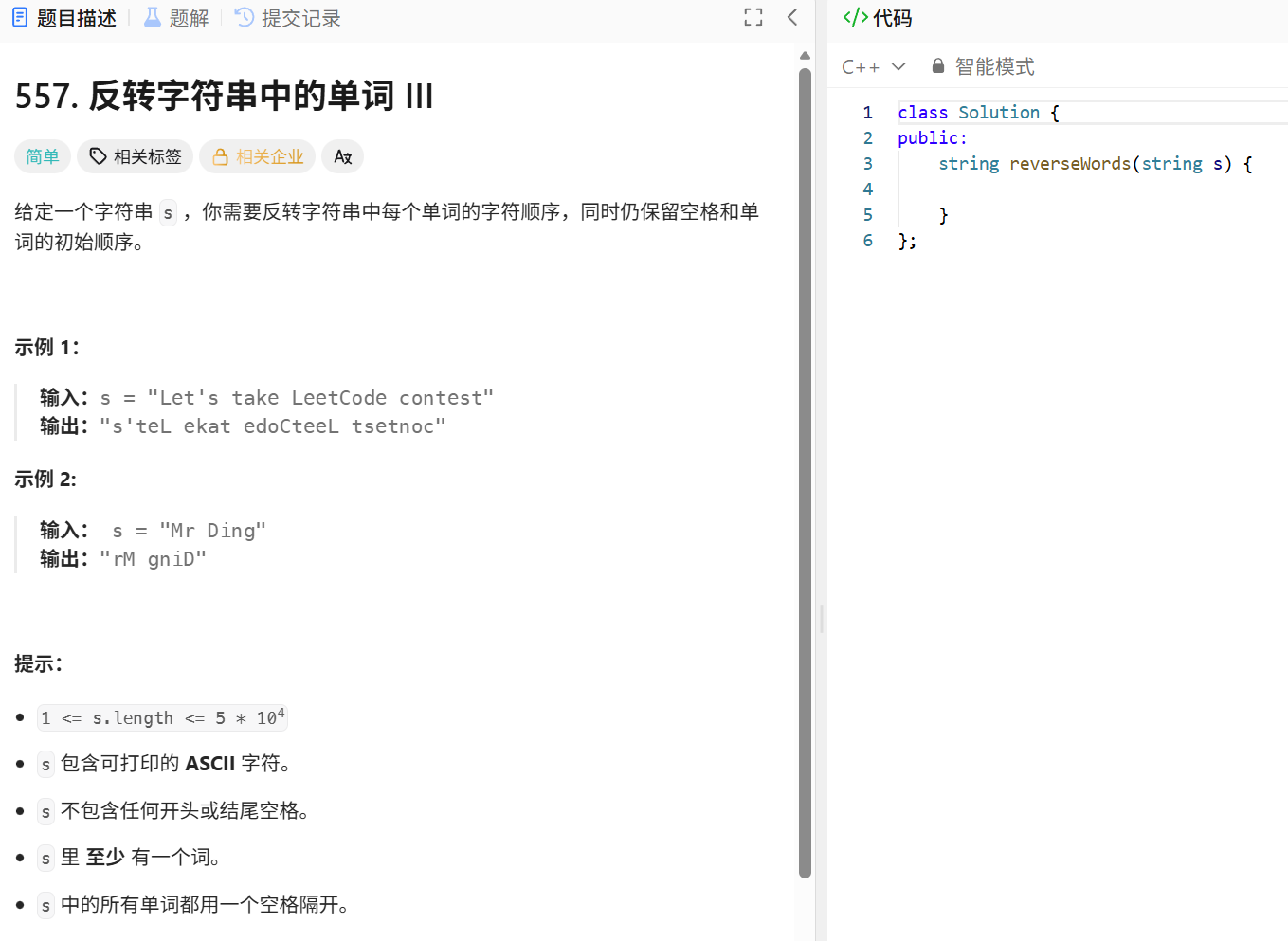
1.9 反转字符串中的单词 |||

反转字符串中的单词 |||

在这里插入图片描述

方法思路 分割单词：利用字符串的空格分隔特性，将输入字符串拆分为多个单词。 反转单词：对每个拆分出的单词，反转其字符顺序。 拼接结果：将反转后的单词按原顺序拼接，并用空格分隔。

在这里插入图片描述

这里说一下题目中的stringstream是干嘛的

1. 库归属 stringstream 是 C++ 标准库中的一个类，定义在 头文件中。它属于 “字符串流” 家族（类似的还有 istringstream 用于仅读取、ostringstream 用于仅写入）。
2. 功能本质 stringstream 的核心是把 “字符串” 当作 “流” 来处理。我们可以像操作 “文件流”“控制台流” 一样，用 >> 从字符串中读取内容，用 << 向字符串中写入内容。
3. 题解中的作用（按空格分割单词） 在题解 stringstream ss(s) 中： 我创建了一个 stringstream 对象 ss，并把输入字符串 s “绑定” 到这个流上。 当执行 ss >> word 时，stringstream 会自动按 “空格” 分割字符串，每次读取一个 “连续的非空格字符段”（即一个单词）到 word 中。 这一步相当于帮省去了 “手动遍历字符串、判断空格、截取单词” 的繁琐过程。

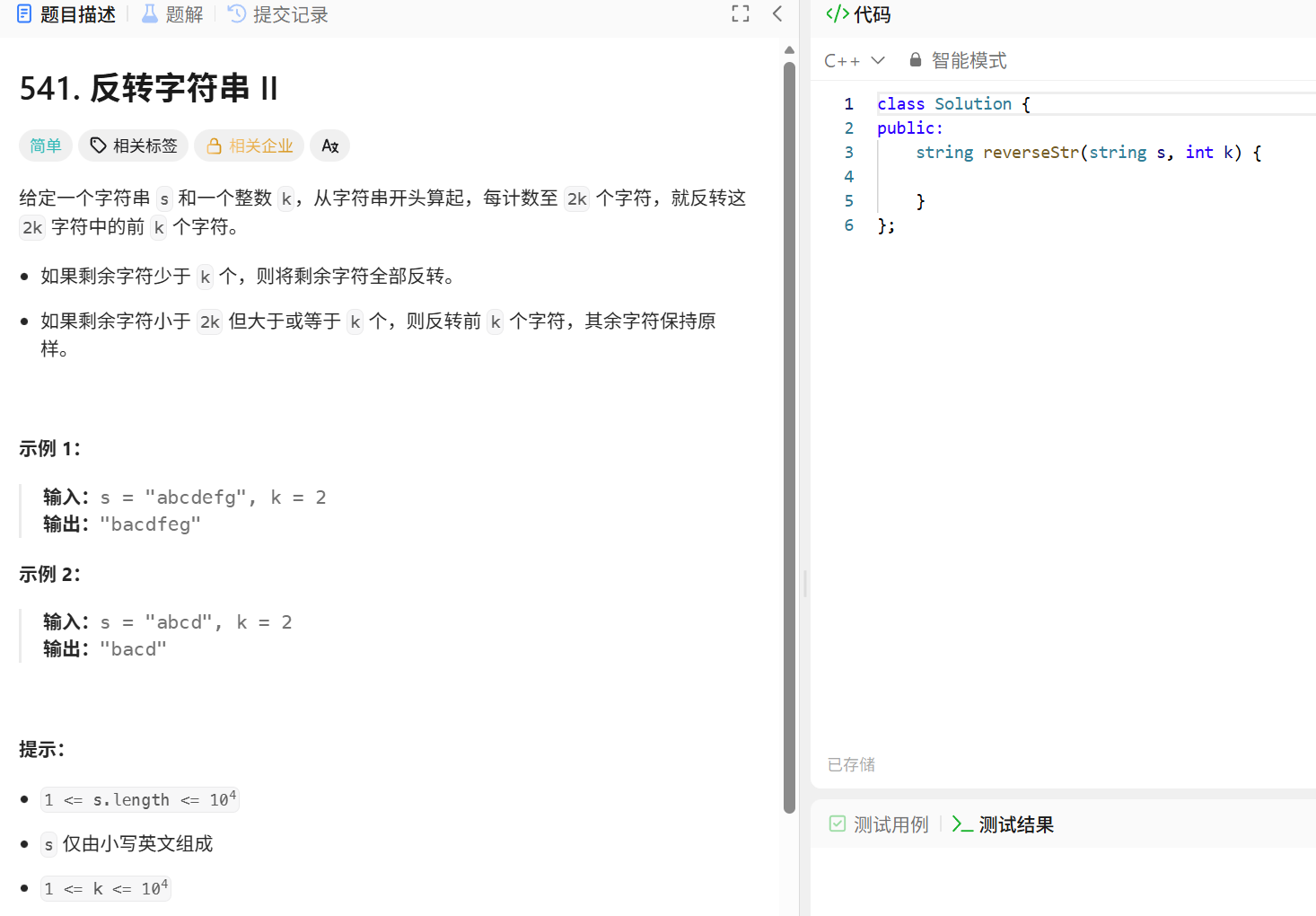
1.10 反转字符串 II

反转字符串 ||

在这里插入图片描述

解题思路 题目要求每 2k 个字符中反转前 k 个字符，并处理两种边界情况。我们可以通过遍历字符串并划定反转区间的方式解决： 遍历步长：以 2k 为步长遍历字符串，确定每个需要处理的大区间起始位置 i。 确定反转区间：对于每个起始位置 i，反转的左边界为 i，右边界为 min(i + k - 1, s.size() - 1)（确保不越界）。 区间内反转：对每个确定的区间 [left, right]，通过双指针交换字符的方式完成反转。

在这里插入图片描述

示例验证

以示例 1 s = "abcdefg", k = 2 为例：
第一次遍历 i = 0，反转区间 [0, 1]（字符 'a' 和 'b'），得到 "bacdefg"。
第二次遍历 i = 4（0 + 2*2），反转区间 [4, 5]（字符 'e' 和 'f'），得到 "bacdfeg"。
剩余字符 'g' 不足 k，无需处理。最终输出与示例一致。
以示例 2 s = "abcd", k = 2 为例：
遍历 i = 0，反转区间 [0, 1]（字符 'a' 和 'b'），得到 "bacd"，与示例输出一致。

在这段代码中，n - 1 是字符串 s 的最后一个字符的索引（因为字符串的索引从 0 开始，长度为 n 的字符串，最大索引是 n-1）。 它的作用是 防止数组越界：当剩余字符数不足 k 个时，i + k - 1 可能会超过字符串的最大有效索引，此时通过 min(i + k - 1, n - 1) 可以确保 right 不会超出字符串的边界，从而避免访问非法内存，保证代码的安全性。 举个例子：如果字符串长度 n = 5（索引 0~4），k = 3，当前 i = 4（剩余字符不足 k），那么 i + k - 1 = 6，但 n - 1 = 4，此时 right 会取 4，确保反转操作仅在有效字符范围内进行。

两种特殊情况的处理体现：

• 对于 “剩余字符少于 k 个，将剩余字符全部反转” 的情况： 若剩余字符数 < k，则 i + k - 1 会超过字符串的最大索引 n - 1，此时 min 函数会取 n - 1 作为 right，即反转区间为 [i, n-1]，实现 “剩余全部反转”。
• 对于 “剩余字符小于 2k 但大于或等于 k 个，反转前 k 个字符” 的情况： 若剩余字符数 ≥k 且 <2k，则 i + k - 1 ≤ n - 1，此时 min 函数会取 i + k - 1 作为 right，即反转区间为 [i, i+k-1]，实现 “反转前 k 个字符”。