【算法基础篇】（五十）扩展中国剩余定理（EXCRT）深度精讲：突破模数互质限制

_OP_CHEN

发布于 2026-01-24 08:46:40

1370

文章被收录于专栏：C++C++

前言

在数论的线性同余方程组求解领域，中国剩余定理（CRT）无疑是经典工具，但它 “模数两两互质” 的严苛前提，让其在面对复杂场景时束手无策。而扩展中国剩余定理（EXCRT）的出现，彻底打破了这一限制 —— 它无需模数互质，能高效求解任意线性同余方程组，成为算法竞赛中处理多模数问题的 “终极武器”。本文将从 CRT 的局限性切入，层层拆解 EXCRT 的迭代合并思想、数学推导与代码实现，手把手教你掌握从理论到实战的全流程，让你在非互质模数方程组问题中轻松破局。下面就让我们正式开始吧！

一、CRT 的痛点：模数不互质怎么办？

1.1 回顾中国剩余定理的局限

经典中国剩余定理的核心前提是所有模数两两互质。例如方程组：

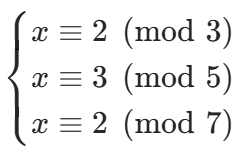
由于 3、5、7 两两互质，CRT 能通过构造法快速求出解。但如果遇到模数不互质的方程组，比如：

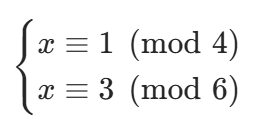
4 和 6 的最大公约数为 2≠1，CRT 的构造法彻底失效 —— 此时无法保证逆元存在，自然无法通过 CRT 的公式求解。而这类非互质模数的方程组，在竞赛中更为常见，EXCRT 正是为解决这类问题而生。

1.2 一个直观的非互质模数方程组示例

我们先看一个简单的非互质模数方程组，感受 EXCRT 的求解场景：

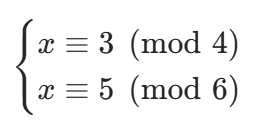
尝试手动求解：

由第一个方程得：x=4k+3（k 为整数）；
代入第二个方程：4k+3≡5(mod 6)，整理得 4k≡2(mod 6)；
简化方程：两边同时除以 2（gcd (4,6)=2），得 2k≡1(mod 3)，解得 k≡2(mod 3)；
因此 k=3t+2，代入 x 的表达式得 x=4(3t+2)+3=12t+11；
最小非负解为 11，验证：11 mod 4=3，11 mod 6=5，完全满足方程组。

这个手动求解过程，其实蕴含了 EXCRT 的核心思想 ——将两个方程合并为一个等价方程，再逐步迭代合并所有方程，最终得到全局解。

二、EXCRT 的核心思想：迭代合并方程

2.1 两个方程的合并原理

EXCRT 的核心是 “化繁为简”：将 n 个线性同余方程逐步合并为 1 个等价的线性同余方程，最终的方程即为原方程组的解。我们先聚焦最基础的两步：合并两个方程。

设两个线性同余方程为：

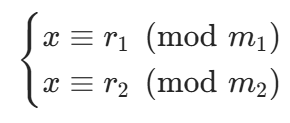
目标：找到一个新的线性同余方程 x≡R(mod M)，使其与原两个方程等价（即解完全相同）。

步骤 1：转化为不定方程

由第一个方程得：x=k1⋅m1+r1（k₁为整数）；将其代入第二个方程：k1⋅m1+r1≡r2(mod m2)；整理得：m1⋅k1≡(r2−r1)(mod m2)。

这是一个关于 k₁的线性同余方程，记为：a⋅k1≡c(mod b)，其中：

a=m1，b=m2，c=(r2−r1)mod m2。

步骤 2：求解线性同余方程

根据裴蜀定理，线性同余方程 a⋅k1≡c (mod b) 有解的充要条件是 gcd(a,b)∣c。设 d=gcd(a,b)：

步骤 3：合并为新方程

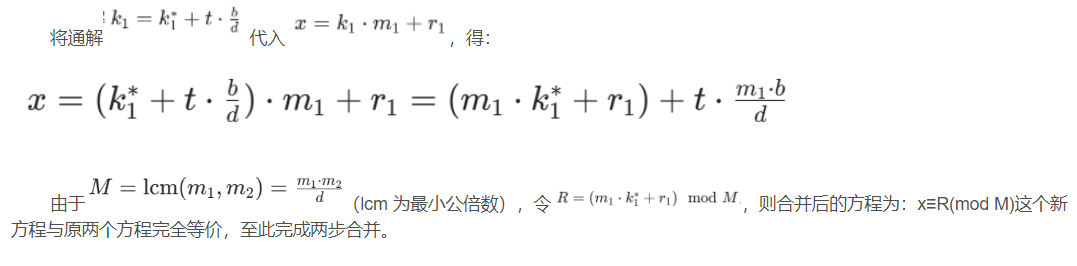
2.2 多方程的迭代合并流程

对于 n 个线性同余方程，EXCRT 的求解流程为：

初始化合并后的方程为 x≡0(mod1)（任何整数都满足此方程，不影响结果）；
依次将当前合并后的方程与第 i 个原始方程合并，得到新的合并方程；
若合并过程中出现无解情况（某一步线性同余方程无解），则整个方程组无解；
合并完所有方程后，最终方程 x≡R(modM) 的最小非负解 R 即为原方程组的最小非负解。

三、核心工具：扩展欧几里得与快速乘

要实现 EXCRT，必须依赖两个核心工具：扩展欧几里得算法（求解线性同余方程）和快速乘（避免大整数溢出）。

3.1 扩展欧几里得算法（exgcd）

扩展欧几里得算法不仅能计算 a 和 b 的最大公约数，还能找到整数 x 和 y，使得 ax+by=gcd(a,b)，是求解线性同余方程的基础。

C++ 实现

#include <iostream>
using namespace std;

typedef long long LL;

// 扩展欧几里得算法：返回gcd(a,b)，通过引用返回ax + by = gcd(a,b)的特解x,y
LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL x1, y1, d = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return d;
}

int main() {
    LL a = 4, b = 6;
    LL x, y;
    LL d = exgcd(a, b, x, y);
    cout << "gcd(" << a << "," << b << ")=" << d << endl;
    cout << "特解：" << a << "*" << x << " + " << b << "*" << y << "=" << d << endl;
    // 输出：gcd(4,6)=2；特解：4*(-1) +6*1=2
    return 0;
}

3.2 快速乘（qmul）

当模数较大时（如 1e9×1e9），直接乘法会超出long long范围导致溢出。快速乘通过将乘法转化为加法，结合模运算，避免溢出。

C++ 实现

// 快速乘：计算(a*b) mod p，避免溢出
LL qmul(LL a, LL b, LL p) {
    LL ret = 0;
    while (b) {
        if (b & 1) {
            ret = (ret + a) % p;
        }
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}

int main() {
    LL a = 1e18, b = 1e18, p = 1e9 + 7;
    cout << qmul(a % p, b % p, p) << endl; // 安全计算(a*b) mod p
    return 0;
}

四、EXCRT 的完整 C++ 实现

结合迭代合并思想、扩展欧几里得算法和快速乘，我们可以写出 EXCRT 的通用实现，适用于任意线性同余方程组（模数可互质或不互质）。

4.1 完整代码

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10; // 支持最多1e5个方程

LL m[N], r[N]; // m[i]为模数，r[i]为余数
int n; // 方程个数

// 扩展欧几里得算法
LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL x1, y1, d = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return d;
}

// 快速乘：防止溢出
LL qmul(LL a, LL b, LL p) {
    LL ret = 0;
    while (b) {
        if (b & 1) ret = (ret + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}

// 扩展中国剩余定理：返回最小非负解，无解返回-1
LL excrt() {
    LL M = 1, ret = 0; // 初始合并方程：x ≡ 0 (mod 1)
    for (int i = 1; i <= n; ++i) {
        LL a = M, b = m[i], c = (r[i] - ret) % b;
        // 确保c为非负
        if (c < 0) c += b;
        // 求解线性同余方程 a*k ≡ c (mod b)
        LL x, y, d = exgcd(a, b, x, y);
        if (c % d != 0) return -1; // 无解
        
        // 计算特解k* = x * (c/d)，并调整为最小正特解
        LL k1 = b / d; // 通解周期
        x = qmul(x, c / d, k1); // 缩放特解，避免溢出
        x = (x % k1 + k1) % k1; // 特解调整为最小正整数
        
        // 更新合并后的方程：x ≡ ret + x*M (mod M*k1)
        ret += x * M;
        M *= k1;
        ret = (ret % M + M) % M; // 确保ret为非负最小解
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    // 输入方程个数
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> m[i] >> r[i];
    }
    
    LL ans = excrt();
    if (ans == -1) {
        cout << "无解" << endl;
    } else {
        cout << "最小非负解：" << ans << endl;
    }
    return 0;
}

4.2 代码分析

时间复杂度：O(nlogM)，其中 n 是方程个数，M 是最终合并后的模数。每个方程的合并过程中，扩展欧几里得和快速乘的时间复杂度均为O(logM)；
空间复杂度：O(n)，仅需存储模数和余数数组，适用于大规模方程组（n≤1e5）；
溢出防护：通过快速乘qmul避免大整数乘法溢出，支持模数乘积达1e18级别；
通用性：无需模数互质，自动处理无解情况，返回最小非负解。

五、实战例题 1：洛谷 P4777 【模板】扩展中国剩余定理

5.1 题目分析

题目链接：https://www.luogu.com.cn/problem/P4777

题目描述：给定 n 组非负整数ai、bi，求解关于 x 的方程组的最小非负整数解：

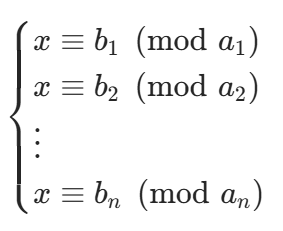
输入描述：第一行一个整数 n，接下来 n 行每行两个非负整数ai、bi。

输出描述：一行一个整数，表示满足条件的最小非负整数 x。

示例输入：311 625 933 17

示例输出：809。

5.2 解题思路

直接套用 EXCRT 模板，将ai作为模数m[i]，bi作为余数r[i]，调用excrt函数即可。

5.3 C++ 实现（模板直接套用）

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;

LL m[N], r[N];
int n;

LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL x1, y1, d = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return d;
}

LL qmul(LL a, LL b, LL p) {
    LL ret = 0;
    while (b) {
        if (b & 1) ret = (ret + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}

LL excrt() {
    LL M = 1, ret = 0;
    for (int i = 1; i <= n; ++i) {
        LL a = M, b = m[i], c = (r[i] - ret) % b;
        if (c < 0) c += b;
        LL x, y, d = exgcd(a, b, x, y);
        if (c % d != 0) return -1;
        LL k1 = b / d;
        x = qmul(x, c / d, k1);
        x = (x % k1 + k1) % k1;
        ret += x * M;
        M *= k1;
        ret = (ret % M + M) % M;
    }
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> m[i] >> r[i];
    }
    cout << excrt() << endl;
    return 0;
}

六、实战例题 2：洛谷 P4774 [NOI2018] 屠龙勇士

题目链接：https://www.luogu.com.cn/problem/P4774

6.1 题目分析

题目描述：玩家需按顺序杀死 n 条巨龙，每条巨龙有初始生命值ai、恢复能力pi。玩家用剑攻击 x 次后，巨龙生命值变为ai−x×ATK，随后巨龙不断恢复pi生命值，直至生命值非负。要求攻击后或恢复过程中生命值恰好为 0，求最小攻击次数 x，无解输出 - 1。

核心转化：

设剑的攻击力为ATK，则需满足 ai−x×ATK+k×pi=0（k 为非负整数）；
整理得线性同余方程：ATK×x≡ai(modpi)；
所有巨龙的方程构成线性同余方程组，求解最小正整数 x。

额外限制：攻击次数 x 需满足 x≥⌈ATKai⌉（否则攻击后生命值仍为正，无法通过恢复变为 0）。

6.2 解题思路

用 set 维护剑的攻击力，为每条巨龙选择符合规则的剑（攻击力不超过生命值的最大剑，无则选最小剑）；
为每条巨龙构建线性同余方程 ATKi×x≡ai(modpi)；
用 EXCRT 求解方程组，得到最小非负解 x；
检查 x 是否满足所有巨龙的攻击次数下限，若不满足则加上通解周期，直至满足。

6.3 C++ 实现（核心部分）

#include <iostream>
#include <set>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;

LL m[N], r[N], a[N]; // m[i]=p_i, r[i]=a_i, a[i]=ATK_i
LL s[N]; // 杀死巨龙后奖励的剑
LL limit; // 攻击次数下限
int n, p;

LL exgcd(LL a, LL b, LL& x, LL& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL x1, y1, d = exgcd(b, a % b, x1, y1);
    x = y1;
    y = x1 - a / b * y1;
    return d;
}

LL qmul(LL a, LL b, LL p) {
    LL ret = 0;
    while (b) {
        if (b & 1) ret = (ret + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return ret;
}

LL excrt() {
    LL M = 1, ret = 0;
    for (int i = 1; i <= n; ++i) {
        LL A = qmul(a[i], M, m[i]);
        LL B = m[i];
        LL C = (r[i] - qmul(a[i], ret, B)) % B;
        if (C < 0) C += B;
        
        LL x, y, D = exgcd(A, B, x, y);
        if (C % D != 0) return -1;
        
        LL k1 = B / D;
        x = qmul(x, C / D, k1);
        x = (x % k1 + k1) % k1;
        
        ret += x * M;
        M *= k1;
        ret = (ret % M + M) % M;
    }
    // 满足攻击次数下限
    if (ret < limit) {
        ret += ((limit - ret + M - 1) / M) * M;
    }
    return ret;
}

void init() {
    limit = 0;
    cin >> n >> p;
    for (int i = 1; i <= n; ++i) cin >> r[i]; // 巨龙生命值a_i
    for (int i = 1; i <= n; ++i) cin >> m[i]; // 恢复能力p_i
    for (int i = 1; i <= n; ++i) cin >> s[i]; // 奖励剑的攻击力
    
    multiset<LL> sword;
    for (int i = 1; i <= p; ++i) {
        LL x;
        cin >> x;
        sword.insert(x);
    }
    
    // 为每条巨龙分配剑
    for (int i = 1; i <= n; ++i) {
        LL hp = r[i];
        auto it = sword.upper_bound(hp);
        if (it != sword.begin()) --it;
        a[i] = *it; // 选中的剑的攻击力
        sword.erase(it);
        sword.insert(s[i]); // 加入奖励的剑
        
        // 计算攻击次数下限：至少需要攻击ceil(hp / a[i])次
        limit = max(limit, (hp + a[i] - 1) / a[i]);
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int T;
    cin >> T;
    while (T--) {
        init();
        LL ans = excrt();
        cout << ans << endl;
    }
    return 0;
}

6.4 代码分析

剑的分配：用 multiset 维护剑的攻击力，支持高效查找和删除，时间复杂度O(nlogm)（m 为初始剑的数量）；
方程构建：每条巨龙对应一个线性同余方程，考虑了攻击力、生命值和恢复能力的关系；
EXCRT 适配：方程左边带有系数（ATK_i），通过快速乘调整系数后再代入 EXCRT 流程；
下限处理：最终解需满足攻击次数下限，通过通解周期调整，确保结果合法。

七、常见误区与避坑指南

7.1 线性同余方程转化错误

误区：将方程 ai−x×ATK≡0(modpi) 错误转化为 ATK×x≡−ai(modpi)，未调整余数符号；
避坑：统一将余数调整为非负，即 c=(r2−r1)modm2，避免负数导致的求解错误。

7.2 溢出防护不到位

误区：直接使用a * b计算，未用快速乘，导致大整数溢出；
避坑：所有涉及模数乘法的地方（如特解缩放、系数调整），均使用快速乘qmul，确保中间结果不溢出。

7.3 忽略无解情况判断

误区：未检查线性同余方程的解的存在性（gcd(a,b)∣c），直接继续合并；
避坑：每次合并方程时，若发现c % d != 0，立即返回 - 1，避免无效计算。

7.4 特解调整错误

误区：求解出特解后未调整为最小正整数，导致合并后的解超出预期；
避坑：通过x = (x % k1 + k1) % k1将特解调整为最小正整数，确保合并后的方程解为最小非负解。

7.5 忘记额外限制条件

误区：求解出方程组的解后，未检查题目中的额外限制（如攻击次数下限）；
避坑：根据题目要求，对 EXCRT 的结果进行二次调整，确保满足所有约束条件。

八、EXCRT 与 CRT 的对比及应用场景

8.1 两者核心对比

特性	中国剩余定理（CRT）	扩展中国剩余定理（EXCRT）
模数要求	必须两两互质	无要求（可互质或不互质）
求解思想	构造法（直接构造全局解）	迭代合并法（逐步合并方程）
时间复杂度	O(nlogM)	O(nlogM)
适用场景	模数互质的方程组	任意线性同余方程组
逆元依赖	依赖逆元存在（模数互质保证）	不依赖全局逆元（仅求解局部逆元）

8.2 EXCRT 的典型应用场景

非互质模数方程组：竞赛中最直接的应用，如洛谷 P4777 模板题；
数论计数问题：结合其他数论知识（如欧拉函数、乘法逆元），求解带多约束的计数问题；
游戏 / 模拟题转化：如屠龙勇士，将实际问题转化为线性同余方程组；
大整数求解：通过多模数约束，构造满足条件的大整数。

总结

扩展中国剩余定理（EXCRT）是突破 CRT 模数互质限制的强大工具，其核心是 “迭代合并方程”—— 将复杂方程组逐步简化为单个等价方程，最终得到全局解。如果在学习过程中遇到具体题目无法解决，或想了解 EXCRT 在更复杂场景（如多变量约束）中的应用，可以随时留言交流。后续将持续更新数论进阶内容，敬请关注！

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2026-01-22，如有侵权请联系 cloudcommunity@tencent.com 删除

工具