部分tucker分解
本文应用部分tucker分解算法对MNIST图像张量数据集(600000,28,28)进行最小化,以保留其在以后应用支持向量机等机器算法时的特征。我有这样的代码,它使张量的第二和第三维最小化。
i = 16
j = 10
core, factors = partial_tucker(train_data_mnist, modes=[1,2],tol=10e-5, rank=[i,j])
train_datapartial_tucker = tl.tenalg.multi_mode_dot(train_data_mnist, factors,
modes=modes, transpose=True)
test_data_partial_tucker = tl.tenalg.multi_mode_dot(test_data_mnist, factors,
modes=modes, transpose=True)当我在使用[i,j]的时候,如何找到最好的秩partial_tucker,这将给图像最好的降维,同时保存尽可能多的数据?
回答 2
Stack Overflow用户
发布于 2021-12-28 21:06:30
与主成分分析一样,当重建的最优均方残差较小时,局部tucker分解也会得到较好的结果。
通常,能够对原始数据进行精确重构的特征( core张量)可以用于进行类似的预测(给定任何模型,我们可以预先进行转换,从core特性重构原始数据)。
import mxnet as mx
import numpy as np
import tensorly as tl
import matplotlib.pyplot as plt
import tensorly.decomposition
# Load data
mnist = mx.test_utils.get_mnist()
train_data = mnist['train_data'][:,0]
err = np.zeros([28,28]) # here I will save the errors for each rank
batch = train_data[::100] # process only 1% of the data to go faster
for i in range(1,28):
for j in range(1,28):
if err[i,j] == 0:
# Decompose the data
core, factors = tl.decomposition.partial_tucker(
batch, modes=[1,2], tol=10e-5, rank=[i,j])
# Reconstruct data from features
c = tl.tenalg.multi_mode_dot(core, factors, modes=[1,2]);
# Calculate the RMS error and save
err[i,j] = np.sqrt(np.mean((c - batch)**2));
# Plot the statistics
plt.figure(figsize=(9,6))
CS = plt.contour(np.log2(err), levels=np.arange(-6, 0));
plt.clabel(CS, CS.levels, inline=True, fmt='$2^{%d}$', fontsize=16)
plt.xlabel('rank 2')
plt.ylabel('rank 1')
plt.grid()
plt.title('Reconstruction RMS error');
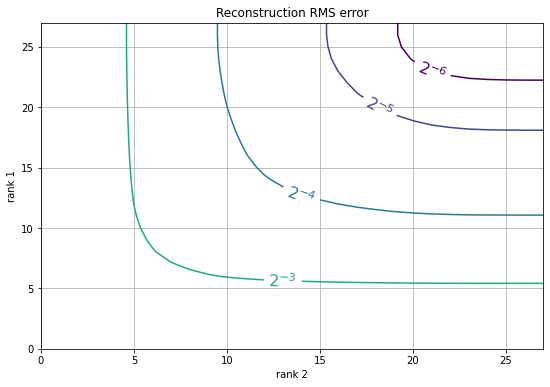
通常你有一个平衡的等级的结果,即i和j没有太大的区别。
随着误差的增加,我们可以得到更好的压缩,我们可以按错误对(i,j)进行排序,并且只绘制给定特征维i * j的误差最小的地方,如下所示
X = np.zeros([28, 28])
X[...] = np.nan;
p = 28 * 28;
for e,i,j in sorted([(err[i,j], i, j) for i in range(1, 28) for j in range(1, 28)]):
if p < i * j:
# we can achieve this error with some better compression
pass
else:
p = i * j;
X[i,j] = e;
plt.imshow(X)
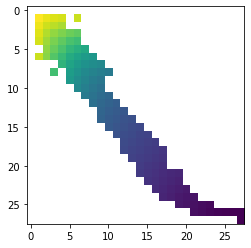
在白色区域的任何地方,你都在浪费资源,选择
Stack Overflow用户
发布于 2021-12-28 21:05:15
因此,如果您查看tensorly链接这里的源代码,您可以看到有关partial_tucker函数的文档中写着:
"""
Partial tucker decomposition via Higher Order Orthogonal Iteration (HOI)
Decomposes 'tensor' into a Tucker decomposition exclusively along
the provided modes.
Parameters
----------
tensor: ndarray
modes: int list
list of the modes on which to perform the decomposition
rank: None, int or int list
size of the core tensor,
if int, the same rank is used for all modes
"""这个函数的目的是为你提供一个近似,为给定的秩保存尽可能多的数据。我不能给你排序“在保存尽可能多的数据的同时,对图像进行最佳降维”,因为维数降低和精度损失之间的最佳折衷是没有客观“正确”答案的,因为它将在很大程度上取决于项目的具体目标和实现这些目标所需的计算资源。
如果我告诉你去做“最佳秩”,它首先就会消除这个近似分解的目的,因为“最佳秩”将是不给出“损失”的秩,它不再是固定秩的近似,它使近似一词变得毫无意义。但是,离这个“最佳等级”有多远才能得到降维,这不是一个其他人可以客观地回答的问题。人们当然可以给出一个意见,但这一意见将取决于比我现在从你那里得到的更多的信息。如果您正在寻找更深入的角度来看待这种权衡,以及什么样的权衡最适合您,我建议在Stack网络中的站点上发布一个关于您的情况的更详细的问题,更多地关注维度降维的数学/统计基础,而不是堆栈溢出所关注的编程方面,例如堆栈Exhange交叉验证或可能的叠外数据科学。
资料来源/参考资料/进一步阅读:
https://stackoverflow.com/questions/70466992
复制相似问题

