约束非线性优化的Matlab fmincon的Python等价
我目前正在尝试实现一个Python脚本,用于解决一个具有大约1000个变量和700个约束条件(包括线性和非线性)的约束非线性优化问题。这个脚本已经有了一个Matlab实现,所以我基本上只是想找到一个与Matlab的fmincon()具有同等性能的Python求解器。
Matlab代码对目标和约束都有解析解,我已经用Python重写了这些解析解。通过从fmincon()调用Python /jacobian函数并确保达到相同的解决方案,我已经验证了Python代码是正确的。作为参考,Matlab代码将以下选项传递给fmincon()
fmincon options:
Options used by current Algorithm ('interior-point'):
(Other available algorithms: 'active-set', 'sqp', 'sqp-legacy', 'trust-region-reflective')
Set properties:
Algorithm: 'interior-point'
CheckGradients: 0
Display: 'none'
HessianApproximation: 'on'
HessianFcn: @(x,lambda)hessian(x,lambda,bCells,d0,rBX,rBY,mask)
MaxFunctionEvaluations: 1000000
MaxIterations: 2000
OptimalityTolerance: 1.0000e-06
SpecifyConstraintGradient: 1
SpecifyObjectiveGradient: 1
Default properties:
BarrierParamUpdate: 'monotone'
ConstraintTolerance: 1.0000e-06
FiniteDifferenceStepSize: 'sqrt(eps)'
FiniteDifferenceType: 'forward'
HessianMultiplyFcn: []
HonorBounds: 1
ObjectiveLimit: -1.0000e+20
OutputFcn: []
PlotFcn: []
ScaleProblem: 0
StepTolerance: 1.0000e-10
SubproblemAlgorithm: 'factorization'
TypicalX: 'ones(numberOfVariables,1)'
UseParallel: 0到目前为止,我已经尝试在scipy.optimize.minimize和cyipopt中使用scipy.optimize.minimize算法,但这两种算法都没有起作用。trust-constr的性能不太好,特别是在参数缩放方面(值较小的变量离最优值很远),而cyipopt根本不收敛。这两个优化器都比fmincon()慢得多。是否还有接近fmincon()性能的其他Python包?
回答 1
Stack Overflow用户
发布于 2022-07-04 23:40:11
有几个high-quality nonlinear programming solvers in Python。从评论上看,这听起来像是一个问题,Hessian或Jacobian在cyipopt中是不正确的。另一种选择是尝试使用建模平台(如pyomo或gekko )来提供衍生产品。下面是fmincon和gekko在相同问题上的比较(Hock Schittkowski #71)。
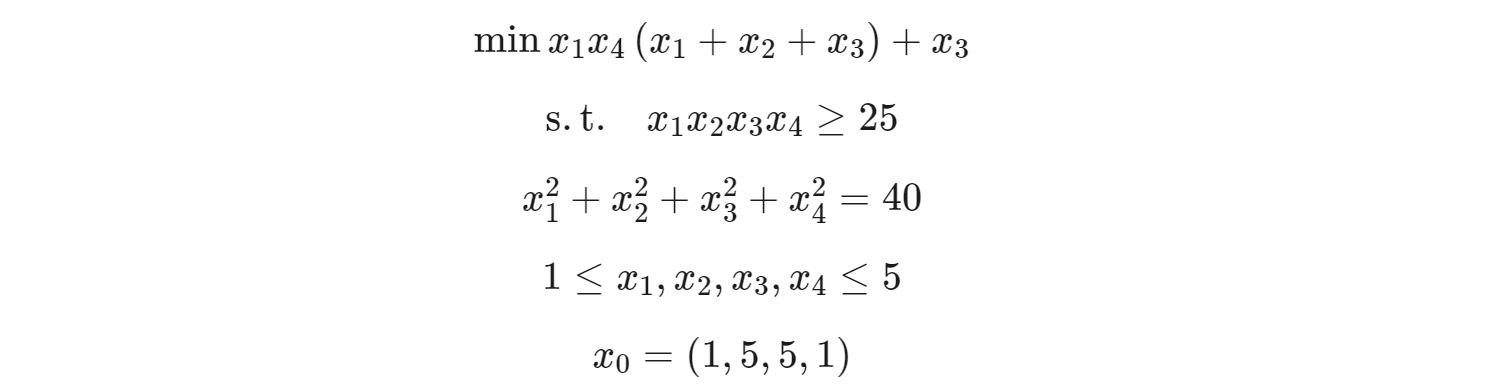
Matlab fmincon
% create file nlcon.m for nonlinear constraints
function [c,ceq] = nlcon(x)
c = 25.0 - x(1)*x(2)*x(3)*x(4);
ceq = sum(x.^2) - 40;objective = @(x) x(1)*x(4)*(x(1)+x(2)+x(3))+x(3);
% initial guess
x0 = [1,5,5,1];
% variable bounds
lb = 1.0 * ones(4);
ub = 5.0 * ones(4);
% linear constraints
A = [];
b = [];
Aeq = [];
beq = [];
% nonlinear constraints
nonlincon = @nlcon;
% optimize with fmincon
%[X,FVAL,EXITFLAG,OUTPUT,LAMBDA,GRAD,HESSIAN]
% = fmincon(FUN,X0,A,B,Aeq,Beq,LB,UB,NONLCON,OPTIONS)
x = fmincon(objective,x0,A,b,Aeq,beq,lb,ub,nonlincon);
% show final objective
disp(['Final Objective: ' num2str(objective(x))])
% print solution
disp('Solution')
disp(['x1 = ' num2str(x(1))])
disp(['x2 = ' num2str(x(2))])
disp(['x3 = ' num2str(x(3))])
disp(['x4 = ' num2str(x(4))])Python
从MATLAB打电话给gekko:
clear all
% Initialize model
m = py.gekko.GEKKO();
% Initialize Variables
x1 = m.Var(pyargs('value',1,'lb',1,'ub',5));
x2 = m.Var(pyargs('value',5,'lb',1,'ub',5));
x3 = m.Var(pyargs('value',5,'lb',1,'ub',5));
x4 = m.Var(pyargs('value',1,'lb',1,'ub',5));
% Define Equations
m.Equation(x1*x2*x3*x4>=25);
m.Equation(x1^2+x2^2+x3^2+x4^2==40);
% Objective
m.Obj(x1*x4*(x1+x2+x3)+x3)
% Solve
m.solve();
% Extract values from Python lists using curly brackets
disp(['x1: ' num2str(x1.VALUE{1})]);
disp(['x2: ' num2str(x2.VALUE{1})]);
disp(['x3: ' num2str(x3.VALUE{1})]);
disp(['x4: ' num2str(x4.VALUE{1})]);用gekko直接用Python (而不是MATLAB)解决优化问题:
from gekko import GEKKO
import numpy as np
m = GEKKO()
x = m.Array(m.Var,4,value=1,lb=1,ub=5)
x1,x2,x3,x4 = x
# change initial values
x2.value = 5; x3.value = 5
m.Equation(x1*x2*x3*x4>=25)
m.Equation(x1**2+x2**2+x3**2+x4**2==40)
m.Minimize(x1*x4*(x1+x2+x3)+x3)
m.solve()
print('x: ', x)
print('Objective: ',m.options.OBJFCNVAL)建模语言将模型编译成字节码,其中包括第一和第二导数的自动微分。它的速度与编译模型后用C或Fortran编写的速度一样快。1000个变量和700个约束条件下的问题通常在几秒钟内解决,这取决于非线性程度。
https://stackoverflow.com/questions/70615264
复制相似问题

