如何在Python中用一些常量的片段进行分段线性拟合？
如何在Python中用一些常量的片段进行分段线性拟合？
提问于 2022-01-14 12:56:07
我试着做一个分段线性拟合，包括3件，其中第一件和最后一件是恒定的。正如你在图中所看到的
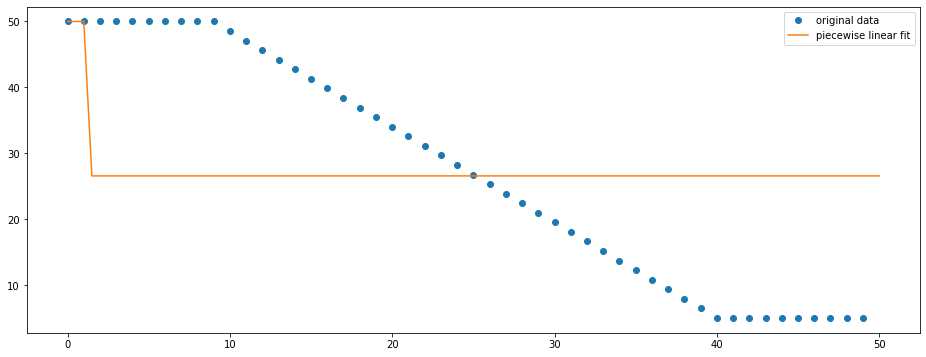
不要得到预期的拟合，因为拟合并不能从原始数据点清晰地捕捉到三个线性部分。
我试着跟踪这个问题，并将其扩展到包含两个常量段的3块情况下，但我肯定做错了什么。
这是我的代码：
from scipy import optimize
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
plt.rcParams['figure.figsize'] = [16, 6]
x = np.arange(0, 50, dtype=float)
y = np.array([50 for i in range(10)]
+ [50 - (50-5)/31 * i for i in range(1, 31)]
+ [5 for i in range(10)],
dtype=float)
def piecewise_linear(x, x0, y0, x1, y1):
return np.piecewise(x,
[x < x0, (x >= x0) & (x < x1), x >= x1],
[lambda x:y0, lambda x:(y1-y0)/(x1-x0)*(x-x0)+y0, lambda x:y1])
p , e = optimize.curve_fit(piecewise_linear, x, y)
xd = np.linspace(0, 50, 101)
plt.plot(x, y, "o", label='original data')
plt.plot(xd, piecewise_linear(xd, *p), label='piecewise linear fit')
plt.legend()对前面提到的问题的公认答案是考虑N个部件的情况下的fit.ipynb，但接下来我似乎无法指定第一个和最后一个片段应该是常量。
此外，我还收到以下警告：
OptimizeWarning: Covariance of the parameters could not be estimated我做错什么了？
回答 3
Stack Overflow用户
回答已采纳
发布于 2022-01-14 14:19:43
您可以直接复制segments_fit实现
from scipy import optimize
def segments_fit(X, Y, count):
xmin = X.min()
xmax = X.max()
seg = np.full(count - 1, (xmax - xmin) / count)
px_init = np.r_[np.r_[xmin, seg].cumsum(), xmax]
py_init = np.array([Y[np.abs(X - x) < (xmax - xmin) * 0.01].mean() for x in px_init])
def func(p):
seg = p[:count - 1]
py = p[count - 1:]
px = np.r_[np.r_[xmin, seg].cumsum(), xmax]
return px, py
def err(p):
px, py = func(p)
Y2 = np.interp(X, px, py)
return np.mean((Y - Y2)**2)
r = optimize.minimize(err, x0=np.r_[seg, py_init], method='Nelder-Mead')
return func(r.x)然后按以下方式应用
import numpy as np;
# mimic your data
x = np.linspace(0, 50)
y = 50 - np.clip(x, 10, 40)
# apply the segment fit
fx, fy = segments_fit(x, y, 3)这将为您提供(fx,fy)角您的分段适合，让我们绘制它
import matplotlib.pyplot as plt
# show the results
plt.figure(figsize=(8, 3))
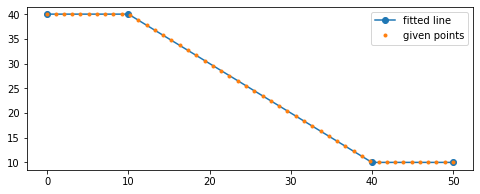
plt.plot(fx, fy, 'o-')
plt.plot(x, y, '.')
plt.legend(['fitted line', 'given points'])
编辑:引入常量段
正如注释中提到的，上面的示例并不保证输出将在结束段中保持不变。
基于这个实现，我认为更简单的方法是限制func(p)这样做，确保段是常量的一种简单方法是设置y[i+1]==y[i]。因此，我添加了xanchor和yanchor。如果给出一个具有重复数字的数组，则可以将多个点绑定到相同的值。
from scipy import optimize
def segments_fit(X, Y, count, xanchors=slice(None), yanchors=slice(None)):
xmin = X.min()
xmax = X.max()
seg = np.full(count - 1, (xmax - xmin) / count)
px_init = np.r_[np.r_[xmin, seg].cumsum(), xmax]
py_init = np.array([Y[np.abs(X - x) < (xmax - xmin) * 0.01].mean() for x in px_init])
def func(p):
seg = p[:count - 1]
py = p[count - 1:]
px = np.r_[np.r_[xmin, seg].cumsum(), xmax]
py = py[yanchors]
px = px[xanchors]
return px, py
def err(p):
px, py = func(p)
Y2 = np.interp(X, px, py)
return np.mean((Y - Y2)**2)
r = optimize.minimize(err, x0=np.r_[seg, py_init], method='Nelder-Mead')
return func(r.x)我对数据生成做了一些修改，以便更清楚地了解更改的影响。
import matplotlib.pyplot as plt
import numpy as np;
# mimic your data
x = np.linspace(0, 50)
y = 50 - np.clip(x, 10, 40) + np.random.randn(len(x)) + 0.25 * x
# apply the segment fit
fx, fy = segments_fit(x, y, 3)
plt.plot(fx, fy, 'o-')
plt.plot(x, y, '.k')
# apply the segment fit with some consecutive points having the
# same anchor
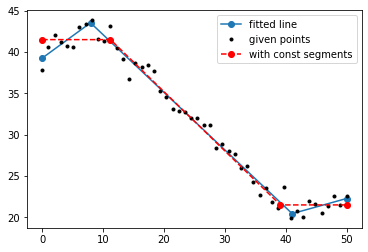
fx, fy = segments_fit(x, y, 3, yanchors=[1,1,2,2])
plt.plot(fx, fy, 'o--r')
plt.legend(['fitted line', 'given points', 'with const segments'])
Stack Overflow用户
发布于 2022-01-16 15:04:45
您可以使用一级的单变量样条得到一行解(不包括导入)。像这样
from scipy.interpolate import UnivariateSpline
f = UnivariateSpline(x,y,k=1,s=0)这里k=1指的是我们用一次线的多项式进行插值。s是平滑参数。它决定了你想在合适的地方妥协多少，以避免使用太多的片段。将其设置为零意味着没有妥协，也就是说，直线必须抛出所有的点数。请参阅文件。
然后
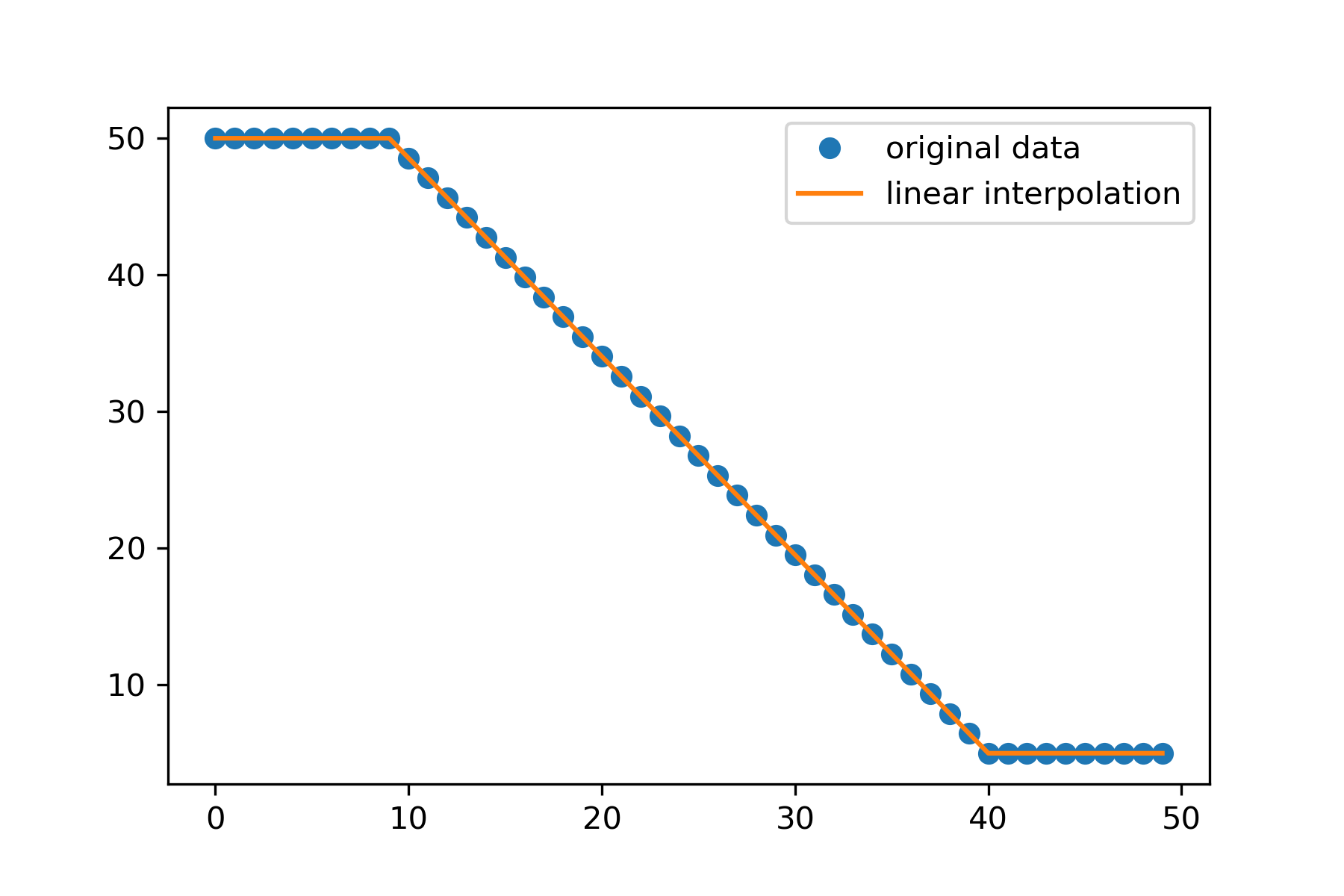
plt.plot(x, y, "o", label='original data')
plt.plot(x, f(x), label='linear interpolation')
plt.legend()
plt.savefig("out.png", dpi=300)给出
Stack Overflow用户
发布于 2022-01-14 16:15:45
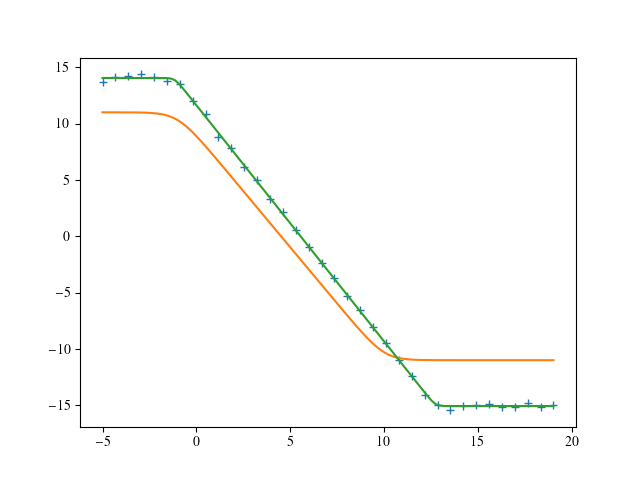
我认为这是一种有趣的非线性方法，效果很好。注意，尽管这是高度非线性的，但它很好地逼近了线性行为。此外，拟合参数提供了线性结果。只对偏移量b进行少量的变换，并根据误差进行传播。(而且，我不关心p的值，只要它略大于5)
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit
np.set_printoptions( linewidth=250, precision=4)
np.set_printoptions( linewidth=250, precision=4)
### piecewise linear function for data generation
def pwl( x, m, b, a1, a2 ):
if x < a1:
out = pwl( a1, m, b, a1, a2 )
elif x > a2:
out = pwl( a2, m, b, a1, a2 )
else:
out = m * x + b
return out
### non-linear approximation
def func( x, m, b, a1, a2, p ):
out = b + np.log(
1 / ( 1 + np.exp( -m *( x - a1 ) )**p )
) / p - np.log(
1 / ( 1 + np.exp( -m * ( x - a2 ) )**p )
) / p
return out
### some data
nn = 36
xdata = np.linspace( -5, 19, nn )
ydata = np.fromiter( (pwl( x, -2.1, 11.6, -1.1, 12.7 ) for x in xdata ), float)
ydata += np.random.normal( size=nn, scale=0.2)
### dense grid for printing
xth = np.linspace( -5, 19, 150 )
###fitting
popt, cov = curve_fit( func, xdata, ydata, p0=[-2, 11, -1, 10, 1])
mF, betaF, a1F, a2F, pF = popt
bF = betaF - mF * a1F
sol=( mF, bF, a1F, a2F, pF )
### transforming the covariance due to the b' -> b mapping
J1 = np.identity(5)
J1[1,0] = -popt[2]
J1[1,2] = -popt[0]
cov2 = np.dot( J1, np.dot( cov, np.transpose( J1 ) ) )
### results
print( cov2 )
for i, v in enumerate( ("m", "b", "a1", "a2", "p" ) ):
print( "{:>2} = {:+2.4e} ± {:0.4e}".format( v, sol[i], np.sqrt( cov2[i,i] ) ) )
### plotting
fig = plt.figure()
ax = fig.add_subplot( 1, 1, 1 )
ax.plot( xdata, ydata, ls='', marker='+' )
ax.plot( xth, func( xth, -2, 11, -1, 10, 1 ) )
ax.plot( xth, func( xth, *popt ) )
plt.show()提供
[[ 1.3553e-04 -7.6291e-04 -4.3488e-04 4.5624e-04 1.2619e-01]
[-7.6291e-04 6.4126e-03 3.4560e-03 -1.5573e-03 -7.4983e-01]
[-4.3488e-04 3.4560e-03 3.4741e-03 -9.8284e-04 -4.2344e-01]
[ 4.5624e-04 -1.5573e-03 -9.8284e-04 3.0842e-03 -5.2739e+00]
[ 1.2619e-01 -7.4983e-01 -4.2344e-01 -5.2739e+00 3.1583e+05]]
m = -2.0810e+00 ± 9.7718e-03
b = +1.1463e+01 ± 6.7217e-02
a1 = -1.2545e+00 ± 5.0384e-02
a2 = +1.2739e+01 ± 4.7176e-02
p = +1.6840e+01 ± 2.9872e+02和
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接：
https://stackoverflow.com/questions/70710906
复制相关文章
相似问题
腾讯云开发者
