可以用时间复杂度O(n)递归地计算Lucas数吗?
可以用时间复杂度O(n)递归地计算Lucas数吗?
提问于 2022-01-31 19:44:29
我有一个作业作业来计算卢卡斯的数字。如何使我的算法O(n)仍然保持递归?
这就是他给出的暗示:
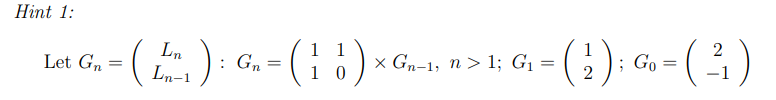
当考虑到这个问题时,我想我会保留我的主for循环,并使它在计算出的一个数字之前存储这两个数字,但这将是迭代的。
这是我现在的代码:
lucas(n) {
return 2 if n = 0;
return 1 if n = 1;
return lucas(n - 1) + lucas(n - 2);
}
main(String args[]) {
for (int i = 0; i<=10; i++)
print(lucas(i*5));
}(代码的编写方式类似于抄袭行为。)
Stack Overflow用户
回答已采纳
发布于 2022-01-31 20:53:23
因为这是家庭作业,所以我不会将解决方案作为代码发布,但我希望我能够显示到它的路径。
给定的提示使用带有两个值的向量--在Java中,我们可以使用数组(因为方法不能只返回两个值)。该方法需要n的值。
int[] calc(int n) {
// TODO
}公式Gn = M X Gn-1 - M是给定的矩阵,Gn = [An , Bn] (An = Ln和Bn = Ln-1)我们可以重写为
[An , Bn] = [[1,1] [1,0]] X [An-1 , Bn-1]或
An = 1*An-1 + 1*Bn-1 = An-1 + Bn-1和
Bn = 1*An-1 + 0*Bn-1 = An-1
该方法将使用n-1调用自己,除非是n == 0,以获得[An-1,Bn-1],然后使用上述公式计算输出数组[An,Bn]。
对于n=0,初始数组应该是[2,-1] (也就是提示中的G0 )。
(由于Gn只依赖于Gn-1,所以纯递归解决方案是O(n) --与通常计算卢卡斯数的方法不同,Ln依赖于Ln-1和Ln-2)
我完全忽略了第二个提示,并使用了上面的int[] -但是不要忘记考虑一个int是否能够表示L500
(有了这个提示就意味着它不会)
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/70931947
复制相关文章
相似问题

