SciPy ODEINT不适用于某些微分方程
SciPy ODEINT不适用于某些微分方程
提问于 2022-02-17 22:10:07
我对Python很陌生,我试图创建2D系统的基本轨迹图。这就是我现在正在做的事。它绘制了一些点的前进轨迹。
import numpy as np
import matplotlib.pyplot as plt
import scipy as sp
from scipy.integrate import odeint
def dx_dt(x,t):
return [x[0]*2, x[1]]
xmin = ymin = -10
xmax = ymax = 10
plt.figure()
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
ts = np.linspace(0,1,20)
ic = np.linspace(xmin, xmax, 11)
for r in ic:
for s in ic:
x0 = [r, s]
xs = sp.integrate.odeint(dx_dt, x0, ts)
plt.plot(xs[:,0], xs[:,1], "g")
plt.savefig("flowlines.jpg")出现的问题是ODEINT不适用于某些系统,而是说了这六次
ODEintWarning:在这个调用上做了过多的工作(可能是错误的Dfun类型)。使用full_output =1运行以获得数量信息。
然后坠毁。
我一直在讨论微分方程的具体系统,我想我已经找到了正在出现的具体问题。有点像
def dx_dt(x,t):
return [x[1], x[0]**2+x[1]]起作用,而
def dx_dt(x,t):
return [x[0], x[1]**2+x[0]]不会的。如果f(x,y)包含除加法和标量乘法以外的任何内容,它似乎不喜欢x‘=f(x,y)的任何特定初始条件。它可以用y做它想做的任何事情,因此,第一个运行得很好,但是第二个失败了,因为y‘= y^2+x包含y的一个幂。
我不知道怎么从这里开始。
回答 1
Stack Overflow用户
发布于 2022-02-17 22:49:35
你怀疑求解者的行为取决于方程的代数形式是合理的。很可能,你正在经历问题的系统是在有限的时间内解决“爆炸”的系统。也就是说,当t接近一个有限值时,一个或两个分量都会达到无穷大。当右边取决于变量的功率时,这很容易发生.
显示这种行为的一个简单的一维系统是
dx/dt = x**2, x(0) = x0它有显式的解决方案
x(t) = x0/(1 - x0*t)您可以验证它是否解决了微分方程和初始条件,至少在t=0附近是这样的。当t x0 1/x0 (假设→≠0)时,解会发散到无穷远。例如,下面是x(0) =0.5的解决方案图:
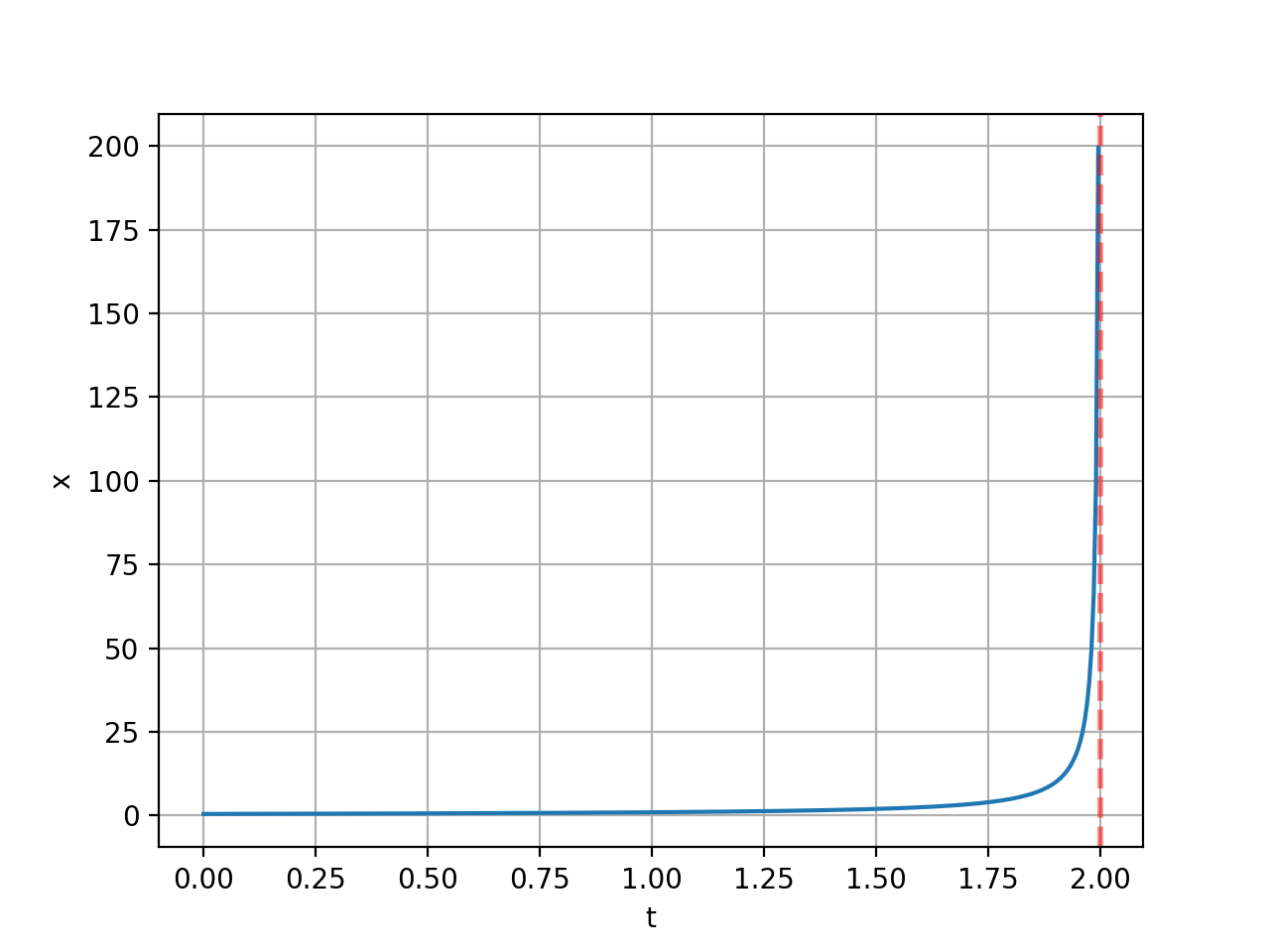
红色垂直虚线表示溶液在哪里爆炸。
这样的方程违反了像odeint这样的ODE求解者所依据的数学假设。求解者通常在遇到这样一个点时会失败,通常是因为他们试图采取越来越小的步骤来降低估计的本地错误,因为当他们接近解决方案崩溃的点时,这是徒劳的:
In [54]: from scipy.integrate import odeint
In [55]: def sys(x, t):
...: return x**2
...:
In [56]: odeint(sys, 0.5, [0, 2.5])
[...]/lib/python3.9/site-packages/scipy/integrate/odepack.py:247:
ODEintWarning: Excess work done on this call (perhaps wrong Dfun type).
Run with full_output = 1 to get quantitative information.
warnings.warn(warning_msg, ODEintWarning)
Out[56]:
array([[5.00000000e-01],
[4.82437777e+08]])解决办法就像那个老笑话的妙语一样:
Patient: Doctor, it hurts when I do this...
Doctor: Then don't do that!页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/71166001
复制相关文章
相似问题

