log_prob与人工计算的差异
log_prob与人工计算的差异
提问于 2022-03-05 21:19:15
在对角线上定义了均值[1, 1, 1]的多元正态分布和0.3的方差协方差矩阵。之后,我要计算数据点[2, 3, 4]上的日志可能性。
通过火炬分布
import torch
import torch.distributions as td
input_x = torch.tensor([2, 3, 4])
loc = torch.ones(3)
scale = torch.eye(3) * 0.3
mvn = td.MultivariateNormal(loc = loc, scale_tril=scale)
mvn.log_prob(input_x)
tensor(-76.9227)从头开始
通过使用对数似然公式:
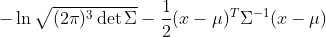
我们得到张量:
first_term = (2 * np.pi* 0.3)**(3)
first_term = -np.log(np.sqrt(first_term))
x_center = input_x - loc
tmp = torch.matmul(x_center, scale.inverse())
tmp = -1/2 * torch.matmul(tmp, x_center)
first_term + tmp
tensor(-24.2842)我用的事实是
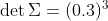
我的问题是-这种差异的根源是什么?
回答 1
Stack Overflow用户
回答已采纳
发布于 2022-03-06 02:02:20
您正在将协方差矩阵传递给scale_tril而不是covariance_matrix。来自PyTorch多元正态的文档
具有正值对角的协方差的下三角因子scale_tril (张量)
因此,将scale_tril替换为covariance_matrix将产生与手动尝试相同的结果。
In [1]: mvn = td.MultivariateNormal(loc = loc, covariance_matrix=scale)
In [2]: mvn.log_prob(input_x)
Out[2]: tensor(-24.2842)然而,作者认为,使用scale_tril更有效:
...Using scale_tril将更有效率:
您可以使用torch.cholesky计算下乔伊尔斯基值。
In [3]: mvn = td.MultivariateNormal(loc = loc, scale_tril=torch.cholesky(scale))
In [4]: mvn.log_prob(input_x)
Out[4]: tensor(-24.2842)页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/71366015
复制相关文章
相似问题

