从scipy.spatial.Delaunay中筛选出简单的滤波器
从scipy.spatial.Delaunay中筛选出简单的滤波器
提问于 2022-03-09 00:10:36
简写版:
是否可以使用现有对象的三角形子集(2D数据)创建一个新的scipy.spatial.Delaunay对象?
我们的目标是在新对象上使用find_simplex方法,并将其过滤掉。
类似但不完全相同的
matplotlib contour/contourf of **concave** non-gridded data
长版本:
我正在查看我用scipy.interpolate.griddata重新处理的lat-lon数据,如下面的伪代码所示:
import numpy as np
from scipy.interpolate import griddata
from scipy.spatial import Delaunay
from scipy.interpolate.interpnd import _ndim_coords_from_arrays
#lat shape (a,b): 2D array of latitude values
#lon shape (a,b): 2D array of longitude values
#x shape (a,b): 2D array of variable of interest at lat and lon
# lat-lon data
nonan = ~np.isnan(lat)
flat_lat = lat[nonan]
flat_lon = lon[nonan]
flat_x = x[nonan]
# regular lat-lon grid for regridding
lon_ar = np.arange(loni,lonf,resolution)
lat_ar = np.arange(lati,latf,resolution)
lon_grid, lat_grid = np.meshgrid(lon_ar,lat_ar)
# regrid
x_grid = griddata((flat_lon,flat_lat),flat_x,(lon_grid,lat_grid), method='nearest')
# filter out extrapolated values
cloud_points = _ndim_coords_from_arrays((flat_lon,flat_lat))
regrid_points = _ndim_coords_from_arrays((lon_grid.ravel(),lat_grid.ravel()))
tri = Delaunay(cloud_points)
outside_hull = tri.find_simplex(regrid_points) < 0
x_grid[outside_hull.reshape(x_grid.shape)] = np.nan
# filter out large triangles ??
# it would be easy if I could "subset" tri into a new scipy.spatial.Delaunay object
# new_tri = ??
# outside_hull = new_tri.find_simplex(regrid_points) < 0问题是凸包的质量很低(很大,在下面的蓝色例子中显示)三角形,我想过滤掉,因为它们不能很好地代表数据。我知道如何在输入点中过滤它们,但不知道如何在网格输出中过滤它们。下面是过滤器函数:
def filter_large_triangles(
points: np.ndarray, tri: Optional[Delaunay] = None, coeff: float = 2.0
):
"""
Filter out triangles that have an edge > coeff * median(edge)
Inputs:
tri: scipy.spatial.Delaunay object
coeff: triangles with an edge > coeff * median(edge) will be filtered out
Outputs:
valid_slice: boolean array that selects "normal" triangles
"""
if tri is None:
tri = Delaunay(points)
edge_lengths = np.zeros(tri.vertices.shape)
seen = {}
# loop over triangles
for i, vertex in enumerate(tri.vertices):
# loop over edges
for j in range(3):
id0 = vertex[j]
id1 = vertex[(j + 1) % 3]
# avoid calculating twice for non-border edges
if (id0,id1) in seen:
edge_lengths[i, j] = seen[(id0,id1)]
else:
edge_lengths[i, j] = np.linalg.norm(points[id1] - points[id0])
seen[(id0,id1)] = edge_lengths[i, j]
median_edge = np.median(edge_lengths.flatten())
valid_slice = np.all(edge_lengths < coeff * median_edge, axis=1)
return valid_slice下面蓝色显示了坏的三角形:
import matplotlib.pyplot as plt
no_large_triangles = filter_large_triangles(cloud_points,tri)
fig,ax = plt.subplot()
ax.triplot(points[:,0],points[:,1],tri.simplices,c='blue')
ax.triplot(points[:,0],points[:,1],tri.simplices[no_large_triangles],c='green')
plt.show()
是否可以只使用scipy.spatial.Delaunay简单程序创建一个新的no_large_triangles对象?目标是使用新对象上的find_simplex方法轻松过滤出点。
作为另一种选择,我怎样才能找到regrid_points中属于蓝色三角形的点的指数?(tri.simplices[~no_large_triangles])
回答 1
Stack Overflow用户
发布于 2022-03-09 20:30:53
因此,可以对Delaunay对象进行修改,以便在一个简单子集上使用find_simplex,但它似乎只适用于蛮力算法。
# filter out extrapolated values
cloud_points = _ndim_coords_from_arrays((flat_lon,flat_lat))
regrid_points = _ndim_coords_from_arrays((lon_grid.ravel(),lat_grid.ravel()))
tri = Delaunay(cloud_points)
outside_hull = tri.find_simplex(regrid_points) < 0
# filter out large triangles
large_triangles = ~filter_large_triangles(cloud_points,tri)
large_triangle_ids = np.where(large_triangles)[0]
subset_tri = tri # this doesn't preserve tri, effectively just a renaming
# the _find_simplex_bruteforce method only needs the simplices and neighbors
subset_tri.nsimplex = large_triangle_ids.size
subset_tri.simplices = tri.simplices[large_triangles]
subset_tri.neighbors = tri.neighbors[large_triangles]
# update neighbors
for i,triangle in enumerate(subset_tri.neighbors):
for j,neighbor_id in enumerate(triangle):
if neighbor_id in large_triangle_ids:
# reindex the neighbors to match the size of the subset
subset_tri.neighbors[i,j] = np.where(large_triangle_ids==neighbor_id)[0]
elif neighbor_id>=0 and (neighbor_id not in large_triangle_ids):
# that neighbor was a "normal" triangle that should not exist in the subset
subset_tri.neighbors[i,j] = -1
inside_large_triangles = subset_tri.find_simplex(regrid_points,bruteforce=True) >= 0
invalid_slice = np.logical_or(outside_hull,inside_large_triangles)
x_grid[invalid_slice.reshape(x_grid.shape)] = np.nan显示新的Delaunay对象只有大三角形的子集。
import matplotlib.pyplot as plt
fig,ax = plt.subplot()
ax.triplot(cloud_points[:,0],cloud_points[:,1],subset_tri.simplices,color='red')
plt.show()
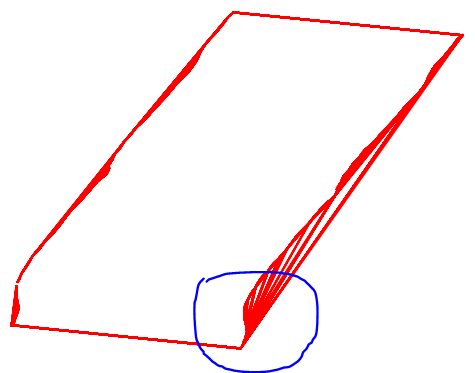
在对大三角形进行过滤之前,用pcolormesh绘制x_grid (在上面的蓝色圆圈中放大):
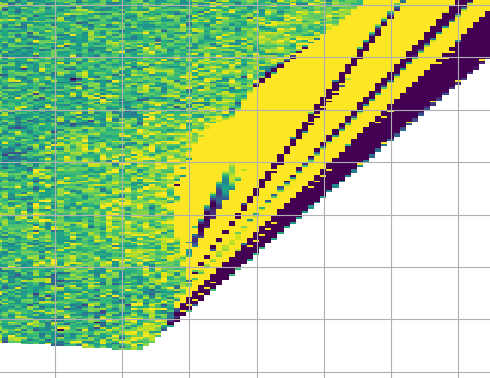
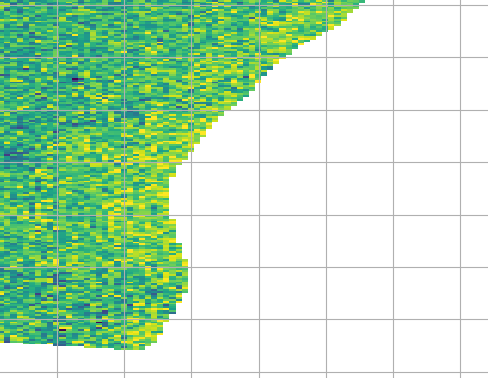
过滤后:
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/71402899
复制相关文章
相似问题

