问将一个大长方体切割成任意尺寸在一定范围内的小长方体。

EN

rng = np.random.default_rng(0)
def split_dimension(length, low, high):
    '''
    Attempt to partition a segment of the given length in segments
    of length between low and high
    '''
    acc = 0
    while length - acc > high:
        assert length - acc >= low, \
          'Failed to get a solution, maybe it was bad luck, maybe there is no solution'
        # of course this choice could be made in a more clever way
        v = rng.uniform(low, high)
        yield acc, v
        acc += v
    yield acc, length - acc

def split_hypercuboid(dimension, dim_ranges):
    '''
    Attempt to split a given cuboid in sub cuboids with dimensions
    
    '''
    low, high = dim_ranges[-1]
    length = dimension[-1] 
    if len(dimension) == 1:
        for c,v in split_dimension(length, low, high):
            yield (c,), (v,)
    else:
        for c,v in split_dimension(length, low, high):
            for corner, size in split_hypercuboid(dimension[:-1], dim_ranges[:-1]):
                yield corner + (c,), size + (v,)
def solve(L, W, H):
    ''' Apply it to the original question '''
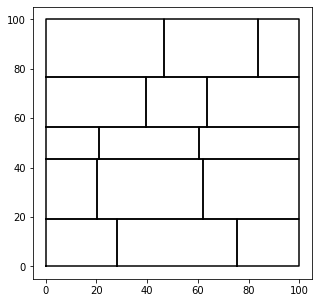
    return list(split_hypercuboid((L, W, H), ((0.2*L, 0.5*L), (0.2*W, 0.5*W), (0.0, 0.3*H))))

绘制第一层

plt.figure(figsize=(5,5))
for (z, x, y), (l, w, h) in solve(100, 100, 100):
    if z == 0:
        plt.plot([x, x, x+w, x+w, x], [y, y+h, y+h, y, y], '-k')

​

​

首先，我们定义了一个计算长度和宽度的随机维数的方法。

# method returns array of random dimensions. Applicable for width and length.
import numpy as np
from math import fsum

def matrix_r(d): # d: dimension of width or legth
    r = np.random.rand(2) * d * 0.3 + 0.2 * d # r initializes with 2 cells
     # tests if the last cell is viable (dimension greater than 20% d)
    while fsum(r) > 0.8 * d:
         # not viable last cell, penultimate is changed to a viable value
         r[1] = np.random.rand(1) * (0.3 * d) + 0.2 * d
     # tests if the solution must have only one or more cells.
    if fsum(r) >= 0.6 * d:
        r = np.append(r, d - fsum(r)) # one cell solves
    else:
         # two cells solve
        r = np.append(r, np.random.rand(1) * d * 0.1 + 0.2 * d)
        r = np.append(r, d - fsum(r))
    return r

在此之后，定义计算高度随机维数组的方法：

def m_he(he):
# method returns array of heights
    hea = np.random.rand(20) * he * 0.3 # initializes with random numbers
     # tailor the array so that the sum is equal to the intended height
    for i in range(3, 20):
        if fsum(hea[0:i]) >= he:
            hea[i - 1] = he - fsum(hea[0: i - 1])
            hea = hea[0: i]
            break
    return hea

因此，定义调用上面定义的方法的方法：

 # method initializes values and calls methods! Return array of cuboid dimensions
def sm_cub(le, wi, he):
    matrix_he = m_he(he)
    matrix_wi = matrix_r(wi)
    matrix_le = matrix_r(le)
    return [(wii, lei, hei) for lei in matrix_le for hei in matrix_he for wii in matrix_wi]

# main
length, width, height = 30, 40, 50
sm_cub(length, width, height)

输出：(每个长方体的尺寸) (13.668186924139675、14.507492472517196、5.867028673417488)、(10.03758244895968、14.507492472517196、5.867028673417488)、(9.171339933891904、14.507492472517196、5.8670283417488)、(7.12289069693008742、14.507492472517196、5.867028673417488)、(13.668186924249675、14.50749242472517196、6.474282800168095)、(10.0375824244895968、14.507492472517196、6.474284500168095)、(9.171339933891904、14.507492424717196、6.4742845008095)、(127.90714.9042、127.90724287505048095)、(9.171339933891904、14.507492472517196、6.4742845008095)。(13.668186924139675，14.507492472517196，11.442336884028546)，(10.03758244895968，14.507492472517196，11.442336884028546)，(9.171339933891904，14.507492472517196，11.442336884028546)，(7.122890693008742，14.507492472517196，11.4423368884028546)，(13.66818692424139675，14.507492472517196，12.406902413723916)，(10.03724244895968，14.507492472517196，12.40749241317196，12.50749241371904，14.50749242472517196，12.40249013916)(127.902424723916)，(10.037242448968，14.5074924717196，12.406492413723904，14.507492424717196，12.640249013916)(127.28902424723916)，(10.037482457968，14.5074972517196，12.40690242413717916)，(14.507399933891904，14.507492424717196，12.640249013916)(127.902427723916)，(10.03724584895968，14.507492472517196)，(12.50649242413723916)，(9.1717133993933891904，14.507492472517196，12.40249013916)(127.902448723916)，(10.03724584895968，14.5074924717196，14.5074924725904，14.5074924717196，14.507492472517196)(1279024487239( 3.453580444916994)、(10.03758244895968、14.507492472517196、3.453580444916994)、(9.171339933891904、14.507492472517196、3.453580444916994)、(7.122890693008742、14.507492472517196、3.453580444916994)、(13.668186924139675、14.507492472517196、10.35586708374444961)、(10.03758244896868、14.507492472517196、10.355867083744961)、(9.1713399338904、14.507492472517196、10.355867083744961)、(7.12289069442、14.507492472517196、10.355867083737961)、(181366.96613.96、166699338904、14.507492472517196、10.3558670837961)、(7.122890694742、14.507492472517196、10.35670837961)、(181366.9661366.9661366.96316633323338964、14.507492472517196、10.35670837961)、(7.1228903008742、14.507492472517196、10.355867083737961)、(1861366.96613.66.9666.9666.96669)、(1662962962963332933638678)、6.633916322946278、5.867028673417488、(9.171339933891904、6.633916322946278、5.867028673417488)、(7.122890693008742、6.633916322946278、5.867028673417488)、(13.668186924139675、6.633916322946278、6.474284500168095)、(10.03758244895968、6.633916322946278、6.474284500168095)、(9.171339933891904、6.63391616322946278、6.474284500168095)、(7.122890693008742、6.633916322946278、6.474284500168095)、(13.668186924139675、6.633916322946278、11.4423368840546)、(10.374866896894868、1144368840546)、(10.37486689683294278)、(6.668186924139675、6.633916322946278、11.4423368840546)(9.171339933891904、6.633916322946278、11.442336884028546)、(7.122890693008742、6.633916322946278、11.442336884028546)、(13.668186924139675、6.633916322946278、12.406902413723916)、(10.03758244895968、6.6339162946278、12.406902413723916)、(9.171339939933891904、6.633916322946278、12.406902413723916)、(7.122890693008742、6.63391616322927278、6.6339902413723916)、(13.66818682424139675、6.633916322946278、3.4580444916994)、(10.024374896.68、33616946278、169293.278、16935935994、16980930994、173399309.04、16933929994)、(17633929994)、(17633929927939)、(16633929994)、(13633929927994)、(13633929927994)、(16633929994)、(10.024374848968)、(1363392992727994)、(13668186924139675)、( 6.633916322946278 )、(3.45804449994)、(10.024374896868)、(13633929927927994)、(13.668186924139675 )、(6.6339162946278)、(3.45804449994)、(10.024374896.68)、(136339299278)、(169359( 3.453580444916994)、(7.122890693008742、6.633916322946278、3.453580444916994)、(13.668186924139675、6.633916322946278、10.355867083744961)、(10.03758244895968、6.633916322946278、10.355867083744961)、(9.171339933891904、6.633916322946278、10.355867083744961)、(7.122890693008742、6.63391632322946278、10.355867083744961)、(13.668186924241375、8.858591204536527、5.867028673417488)、(10.0375824485968、8.8585912045527、5.862870673417488)、(179.1339938.89988.04、2858585858585303757373748488)、(179.3839998.89988.08)、(28586867341748484868)、(10.037582495968)、(8.8585860453474868)、(10.037582495968)、(8.85858684545174868)、(5.037582495968)、(5.863858244895968)、(5.8375824485968)、(5.86287067371748488)、(179.38399904)、(28585988.04)、(2858583737374878)、(10.037582495968)、(8.85858244895968)、(5.863858244894868)、(8.037582495968)、(8.8585998.04)、(5.862868673717488)、(10.0375824959688.858591204536527，5.867028673417488，(13.668186924139675，8.858591204536527，6.474284500168095)，(10.03758244895968，8.858591204536527，6.474284500168095)，(9.171339933891904，8.858591204536527，6.474284500168095)，(7.122890693008742，8.858591204536527，6.474282800168095)，(13.66818692424139675，8.858591204536527，11.442336886884028546)，(10.03758244895968，8.8585912045527，8.442336884028546)，(9.173993381904，8.8591204536527，11.233328546)，(28858684845542)，(10.03758244896868)，(9.1739933891904，8.8591204536527，11.2334057.46)，(2888.8988.6888027)，(8.837582448968)，(9.173993391904，8.8591204536527，11.2334057.46,2888.8988.8988.3988.3988027)。(13.668186924139675、8.858591204536527、12.406902413723916)、(10.03758244895968、8.858591204536527、12.406902413723916)、(9.171339933891904、8.858591204536527、12.406902413723916)、(7.122890693008742、8.858591204536527、12.406902413723916)、(13.66868186924139675、8.858591204536527、3.453580444916994)、(10.03758244895968、8.8581204536527、8.85880444916527)、(9.1713399338904、8.8585912045527、3.453580444916994)、(127.28908742)、(127.28908742)、(127.28908742)、(127.28908742)、(127.28908742)、(127.28908742)、(127.28908742)、(127.28908742)、(127.28908742)、(1648595945927)、(13448845994)、(1344888.994)、(1.1713399338904)、(8.8585912045527)、(9.1713399338904、8.8585912045527、3.453580444916994)。10.355867083744961，(10.03758244895968，8.858591204536527，10.355867083744961)，(9.171339933891904，8.858591204536527，10.355867083744961)，(7.122890693008742，8.858591204536527，10.355867083744961)