K-方法++的实现细节
K-方法++的实现细节
提问于 2022-04-28 18:03:47
我在做K-意思是使用MINST数据集。然而,我发现在初始化的实现和一些进一步的步骤方面存在困难。
对于初始化,我必须首先选择一个随机数据点到第一个质心。然后,对于剩余的质心,我们也随机选择数据点,但从加权概率分布,直到所有的质心被选择。
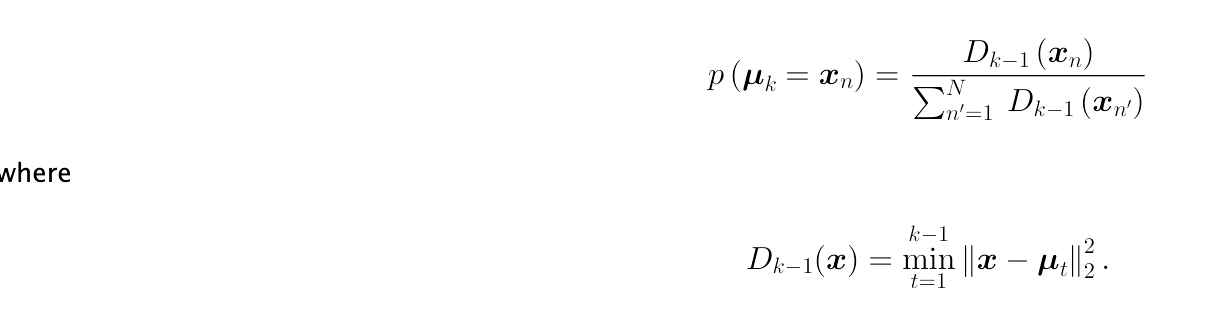
我坚持这一步,如何应用这个发行版来选择?我是说,如何实现它?对于D_{k-1}(x),我可以只使用np.linalg.norm编译并整理它吗?
对于我的实现,我现在只是初始化了第一个元素
self.centroids = np.zeros((self.num_clusters, input_x.shape[1]))
ran_num = np.random.choice(input_x.shape[0])
self.centroids[0] = input_x[ran_num]
for k in range(1, self.num_clusters):下一步,我是否需要通过获取前质心点与所有样本点之间的最大距离来找到下一个质心?
回答 1
Stack Overflow用户
发布于 2022-04-30 10:37:35
您需要创建一个分布,其中选择一个观察的概率是观察与其最近的集群之间的(规范化)距离。因此,要选择一个新的聚类中心,就有很高的概率来选择远不是所有现有的簇中心的观测。同样,选择接近现有星系团中心的观测的可能性也很低。
这个应该是这样的:
centers = []
centers.append(X[np.random.randint(X.shape[0])]) # inital center = one random sample
distance = np.full(X.shape[0], np.inf)
for j in range(1,self.n_clusters):
distance = np.minimum(np.linalg.norm(X - centers[-1], axis=1), distance)
p = np.square(distance) / np.sum(np.square(distance)) # probability vector [p1,...,pn]
sample = np.random.choice(X.shape[0], p = p)
centers.append(X[sample])页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/72048356
复制相关文章
相似问题

