如何避免numpy中的NAN值?
如何避免numpy中的NAN值?
提问于 2022-05-28 21:07:08
我有一个非线性的PDE系统,我试图用有限差分法来求解它。但是我不断地得到以下错误,而这些图形是不正确的:
RuntimeWarning:除以在double_scalars中遇到的零
我的代码如下:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
Lx = 1.0
Ly = 1.0
Time = 4 #Integration time
#constants :
D = 0.001
xi0=0.38
gho = 0.34
alpha = 0.6
mu = 0.1
beta = 0.05
gamma = 0.1
# NUMERICAL PARAMETERS
NX = 100
NT = 100
dx = Lx/(NX-1)
dt = Time/NT
#initial conditions
def n0(x, y):
return np.exp(-1*(x**2)/(0.001))*(np.sin(6*np.pi*y))**2
def c0(x,y):
return np.exp(-1*(1-x)**2/0.45)
def f0(x,y):
return 0.75*np.exp(-1*(x)**2/0.45)
def xi(y):
return xi0/(1+alpha*y)
def grad(x,y,a):
p = np.array([(y-x)/dx,(y-a)/dx])
return p
def laplacien(a,b,c,d,f):
s = (a+c+d+f-4*b)/(dx**2)
return s
def G(Z,j,i):
n = Z[0]
f = Z[1]
c = Z[2]
d21 = laplacien(n[j-1,i],n[j,i],n[j+1,i],n[j,i-1],n[j,i+1])
d22 = laplacien(f[j-1,i],f[j,i],f[j+1,i],f[j,i-1],f[j,i+1])
d23 = laplacien(c[j-1,i],c[j,i],c[j+1,i],c[j,i-1],c[j,i+1])
d11 = grad(n[j-1,i],n[j,i],n[j,i-1])
d12 = grad(f[j-1,i],f[j,i],f[j,i-1])
d13 = grad(c[j-1,i],c[j,i],c[j,i-1])
d14 = grad(xi(c[j-1,i]),xi(c[j,i]),xi(c[j,i-1]))
n[j,i] +=dt*(D*d21 -(np.dot(d14,d13) + xi(c[j,i])*d23 +gho*d22)*n[j,i]-np.dot((xi(c[j,i])*d13 + gho*d12),d11))
f[j,i] += dt*(beta-gamma*f[j,i])*n[j,i]
c[j,i] += -dt*mu*n[j,i]*c[j,i]
I = np.linspace(0,1,NX)
J = np.linspace(0,1,NX)
X,Y = np.meshgrid(I,J)
N = n0(X,Y)
F = f0(X,Y)
C = c0(X,Y)
A = np.array([N,F,C])
for n in range(1,NT+1):
for j in range (1, NX-1):
for i in range(1, NX-1):
G(A,j,i)
N1 = A[0]
F1 = A[1]
C1 = A[2]
for i in range(1, NX-1):
d1 = (N1[2,i]-N1[1,i])/dx
d2 = (F1[2,i]-F1[1,i])/dx
d3 = (C1[2,i]-C1[1,i])/dx
d4 = (N1[NX-1,i]-N1[NX-2,i])/dx
d5 = (F1[NX-1,i]-F1[NX-2,i])/dx
d6 = (C1[NX-1,i]-C1[NX-2,i])/dx
ki = xi(C1[0,i])*d3 + gho*d2
N1[0,i] = D*d1/ki
kf = xi(C1[NX-1,i])*d6 + gho*d5
N1[NX-1,i] = D*d4/kf
for j in range (1, NX-1):
d1 = (N1[j,2]-N1[j,1])/dx
d2 = (F1[j,2]-F1[j,1])/dx
d3 = (C1[j,2]-C1[j,1])/dx
d4 = (N1[j,NX-1]-N1[j,NX-2])/dx
d5 = (F1[j,NX-1]-F1[j,NX-2])/dx
d6 = (C1[j,NX-1]-C1[j,NX-2])/dx
ki = xi(C1[j,0])*d3 + gho*d2
N1[j,0] = D*d1/ki
kf = xi(C1[j,NX-1])*d6 + gho*d5
N1[j,NX-1] = D*d4/kf
if (n%25 == 0):
fig = plt.figure()
ax = plt.axes()
plt.imshow(N1
, origin='lower'
, cmap='RdGy'
)
plt.colorbar()
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
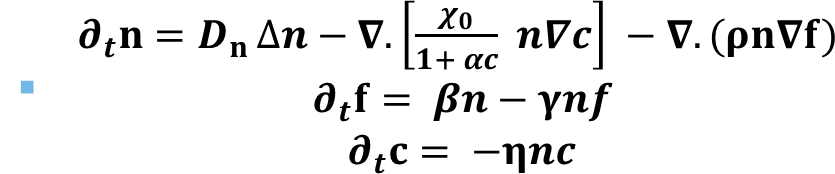
我的问题是:是否有一种方法来做有限差分法,这样NAN值就不会出现,或者这种方法不适用于PDE非线性系统?
回答 1
Stack Overflow用户
发布于 2022-05-29 02:08:06
您可以尝试的方法之一是向除数添加一个非常小的值。
找到发生除以零的行,并将y/x形式的代码更改为表单y/(x+1e-5)。
调整小数字的大小,注意正在处理的数字的范围。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/72419272
复制相关文章
相似问题

