R中具有二元选择变量的整数优化
R中具有二元选择变量的整数优化
提问于 2022-06-23 22:09:45
我正在处理一个优化问题,在这个优化问题中,我的选择变量(是否构建)是一个二进制变量。所附照片显示了最优的构建选择(使用Excel中的Solver解决)。
我试图在R中复制这个问题,将预算约束为≤30的期望值之和(EV)最小化,并构建选项作为选择变量。
问题是EV随着给定的构建决策组合而变化。它的一般公式是:
EV =火灾概率(P)*伤害(火灾时)+(1-p)*伤害(无火灾)+成本(K)。
当没有火灾时,伤害为0。当有火灾和地块没有塔时的伤害很高,当地块上建了一座塔的时候伤害很小。
因此EV =p*伤害(火灾状态)+成本
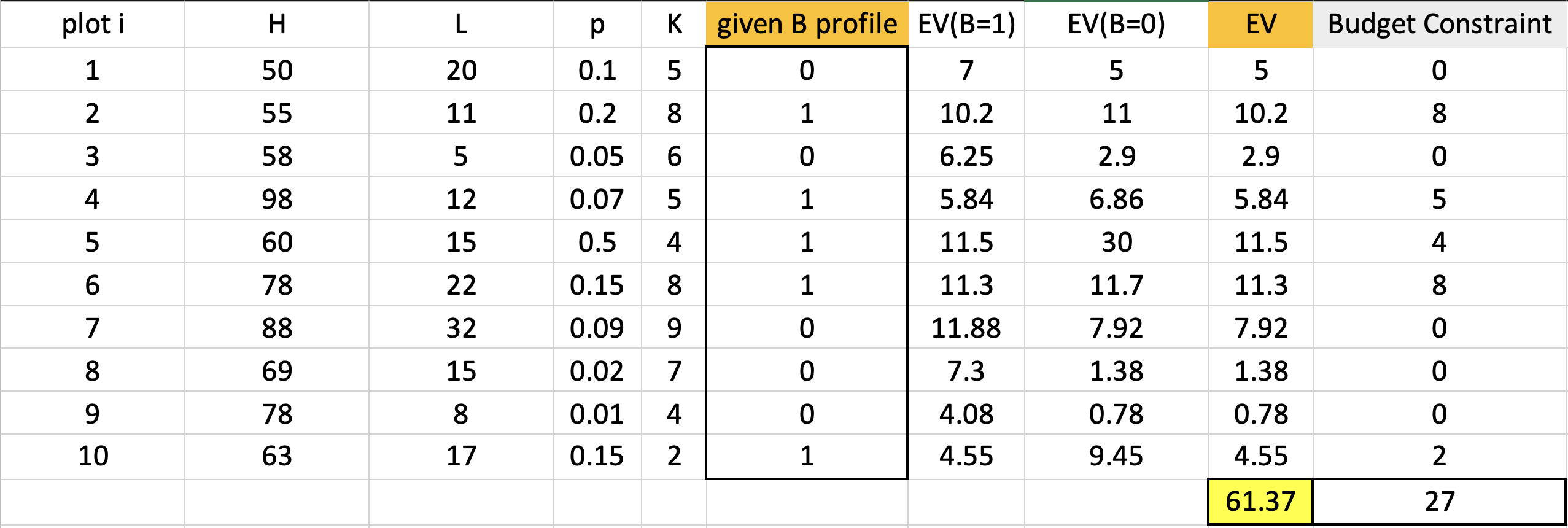
地块一:十块土地(大小或其他属性不重要)。H:高损坏。只有在没有建造决定的情况下,才会造成高伤害。低损伤。如果我们选择在给定的地块上建造一座塔,就会造成很低的伤害。p:开火的概率。K:建造了望塔的费用。给定B配置文件:B是一个二进制变量。B=1表示我们选择在给定的地块中构建。EV(B=1):如果我们选择构建的话,期望值。EV(B=0):如果我们不构建的话,期望值。EV:最终期望值。如果我们构建EV = EV(B=1),则EV = EV(B=0)。预算约束:如果我们建造,它等于建筑成本,否则它是0。
回答 1
Stack Overflow用户
回答已采纳
发布于 2022-06-25 17:07:26
通过为每一行设置两个变量,您可以将问题表示为二进制线性问题。这一对变量以下列方式连接:
- 他们的成本是EV1和EV0
- 他们的预算是K和0
- 他们的总和正好是1
数据
data <- data.frame(
H = c(50, 55, 58, 98, 60, 78, 88, 69, 78, 63),
L = c(20, 11, 5, 12, 15, 22, 32, 15, 8, 17),
p = c(0.1, 0.2, 0.05, 0.07, 0.5, 0.15, 0.09, 0.02, 0.01, 0.15),
K = c(6, 8, 6, 5, 4, 8, 9, 7, 4, 2)
)
data$EV1 <- data$L * data$p + data$K
data$EV0 <- data$H * data$p溶液
library(lpSolve)
n <- nrow(data)
total_budget <- 30
res <- lp(
direction = "min",
objective = c(data$EV1, data$EV0),
const.mat = rbind(c(data$K, rep(0, n)), cbind(diag(n), diag(n))),
const.dir = c("<=", rep("=", n)),
const.rhs = c(total_budget, rep(1, n)),
all.bin = TRUE
)
res$solution[seq_len(n)]
[1] 0 1 0 1 1 1 0 0 0 1
res$objval
[1] 61.37
sum(data$K[res$solution[seq_len(n)] == 1])
[1] 27其中total_budget是您预算的上限。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/72737088
复制相关文章
相似问题

