对两个不同的物理对象使用带有zip/unzip的笨拙数组
我试图在希格斯粒子->4轻子通道中复制部分希格斯粒子发现,利用公开的数据和利用awkward。我可以这样做,当轻子是相同的(例如,4个μ子)与zip/解压缩,但有没有办法做它在2μ子/2电子通道?我从HSF教程中的示例开始。
https://hsf-training.github.io/hsf-training-scikit-hep-webpage/04-awkward/index.html
因此,我现在有以下几点。首先获取输入文件
curl http://opendata.cern.ch/record/12361/files/SMHiggsToZZTo4L.root --output SMHiggsToZZTo4L.root然后我做以下几件事
import numpy as np
import matplotlib.pylab as plt
import uproot
import awkward as ak
# Helper functions
def energy(m, px, py, pz):
E = np.sqrt( (m**2) + (px**2 + py**2 + pz**2))
return E
def invmass(E, px, py, pz):
m2 = (E**2) - (px**2 + py**2 + pz**2)
if m2 < 0:
m = -np.sqrt(-m2)
else:
m = np.sqrt(m2)
return m
def convert(pt, eta, phi):
px = pt * np.cos(phi)
py = pt * np.sin(phi)
pz = pt * np.sinh(eta)
return px, py, pz
####
# Read in the file
infile_name = 'SMHiggsToZZTo4L.root'
infile = uproot.open(infile_name)
# Convert to Cartesian
muon_pt = infile_signal['Events/Muon_pt'].array()
muon_eta = infile_signal['Events/Muon_eta'].array()
muon_phi = infile_signal['Events/Muon_phi'].array()
muon_q = infile_signal['Events/Muon_charge'].array()
muon_mass = infile_signal['Events/Muon_mass'].array()
muon_px,muon_py,muon_pz = convert(muon_pt, muon_eta, muon_phi)
muon_energy = energy(muon_mass, muon_px, muon_py, muon_pz)
# Do the magic
nevents = len(infile['Events/Muon_pt'].array())
# nevents = 1000 # For testing
max_entries = nevents
muons = ak.zip({
"px": muon_px[0:max_entries],
"py": muon_py[0:max_entries],
"pz": muon_pz[0:max_entries],
"e": muon_energy[0:max_entries],
"q": muon_q[0:max_entries],
})
quads = ak.combinations(muons, 4)
mu1, mu2, mu3, mu4 = ak.unzip(quads)
mass_try = (mu1.e + mu2.e + mu3.e + mu4.e)**2 - ((mu1.px + mu2.px + mu3.px + mu4.px)**2 + (mu1.py + mu2.py + mu3.py + mu4.py)**2 + (mu1.pz + mu2.pz + mu3.pz + mu4.pz)**2)
mass_try = np.sqrt(mass_try)
qtot = mu1.q + mu2.q + mu3.q + mu4.q
plt.hist(ak.flatten(mass_try[qtot==0]), bins=100,range=(0,300));柱状图看上去不错!
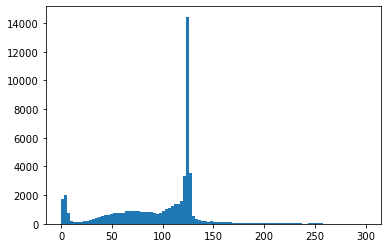
那么,对于2-电子+2-μ子组合,我如何做到这一点?我想有一种方法可以制作lepton_xxx数组吗?但我不知道如何做到这一点,优雅(快速),以便我也可以创建一个标志,以跟踪轻子组合是什么?
谢谢!
哑光
Stack Overflow用户
发布于 2022-07-01 21:42:40
这一问题可以通过多种方式加以解决:
- 制作电子和μ子的联合数组(混合数据类型)。
- 制作一个电子和μ子阵列,这些电子和μ子类型相同,但有一个标志来表示风味(电子对μ子)
- 对μ子使用ak.combinations和
n=2,对电子使用ak.combinations和n=2,然后将它们与ak.cartesian结合起来(处理元组的元组,而不是一个元组,这意味着对ak.unzip的两个调用)。 - 将电子和μ子集合分解成单电荷集合。你需要一个正μ子,一个负μ子,一个正电子,一个负电子,这是四个集合的一个ak.cartesian。
我将采用最后一种方法,因为我认为这是最简单的方法。
您可能想知道的另一件事是向量库。之后
import vector
vector.register_awkward()您不必进行显式坐标转换或质量计算。我会用这个的。以下是我在数据中的阅读方式:
infile = uproot.open("/tmp/SMHiggsToZZTo4L.root")
muon_branch_arrays = infile["Events"].arrays(filter_name="Muon_*")
electron_branch_arrays = infile["Events"].arrays(filter_name="Electron_*")
muons = ak.zip({
"pt": muon_branch_arrays["Muon_pt"],
"phi": muon_branch_arrays["Muon_phi"],
"eta": muon_branch_arrays["Muon_eta"],
"mass": muon_branch_arrays["Muon_mass"],
"charge": muon_branch_arrays["Muon_charge"],
}, with_name="Momentum4D")
electrons = ak.zip({
"pt": electron_branch_arrays["Electron_pt"],
"phi": electron_branch_arrays["Electron_phi"],
"eta": electron_branch_arrays["Electron_eta"],
"mass": electron_branch_arrays["Electron_mass"],
"charge": electron_branch_arrays["Electron_charge"],
}, with_name="Momentum4D")这再现了你的情节:
quads = ak.combinations(muons, 4)
quad_charge = quads["0"].charge + quads["1"].charge + quads["2"].charge + quads["3"].charge
mu1, mu2, mu3, mu4 = ak.unzip(quads[quad_charge == 0])
plt.hist(ak.flatten((mu1 + mu2 + mu3 + mu4).mass), bins=100, range=(0, 200));
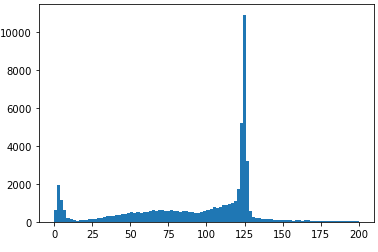
引用的数字片(例如"0"和"1")选择元组字段,而不是数组条目;这是一个手动ak.unzip。(如果我向fields提供了一个ak.combinations参数,这些字段可能有实名。)
对于这两个μ子,两个电子,让我们形成四个不同的集合。
muons_plus = muons[muons.charge > 0]
muons_minus = muons[muons.charge < 0]
electrons_plus = electrons[electrons.charge > 0]
electrons_minus = electrons[electrons.charge < 0]ak.combinations函数(默认为axis=1)返回列表数组中每个列表的笛卡儿乘积,不包括带有自身的项、(x, x) (除非需要,指定replacement=True),而不包括每个对称对(x, y)/(y, x)中的一个。
如果您只想要一个简单的笛卡儿积,一个数组的列表和另一个数组的列表,那就是ak.cartesian。这四个集合muons_plus,muons_minus,electrons_plus,electrons_minus是不重叠的,我们希望每个四轻子群都有一个,所以这是一个简单的笛卡尔积。
mu1, mu2, e1, e2 = ak.unzip(ak.cartesian([muons_plus, muons_minus, electrons_plus, electrons_minus]))
plt.hist(ak.flatten((mu1 + mu2 + e1 + e2).mass), bins=100, range=(0, 200));
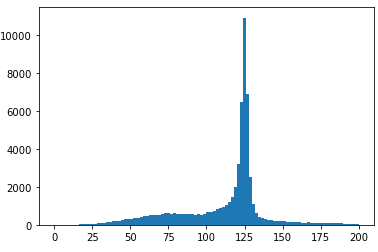
用香料(电子对μ子)而不是电荷来分离粒子是C++施加的分型约束的产物。电子以不同的方式从μ子中测量出来,因此它们在数据集中有不同的属性。在静态类型语言(如C++ )中,我们不能将它们放在同一个集合中,因为它们按类型不同(有不同的属性)。但是收费只因值(整数)不同而不同,因此没有理由将它们放在不同的集合中。
但是现在,区别类型的唯一方法是:(a)对象具有哪些属性,(b)使用该属性集命名什么对象。在这里,我给它们命名为"Momentum4D",因为这允许向量将它们识别为洛伦兹向量,并给出洛伦兹向量方法。但它们可以有其他属性(例如,电子的e_over_p,而不是μ子)。charge是一个非Momentum4D属性。
所以,如果我们要在不同的阵列中放置不同口味的轻子,为什么不把不同的电荷轻子也放在不同的阵列中呢?物理上,风味和电荷都是粒子性质在同一层次上的区别,所以我们可能想要这样做的分析。没有理由让C++类型的区别妨碍分析逻辑!
另外,你可能想
nevents = infile["Events"].num_entries若要从TTree中获取条目数,而不读取数组数据,请执行以下操作。
https://stackoverflow.com/questions/72834275
复制相似问题

