固定参数回归的最小平方误差
固定参数回归的最小平方误差
提问于 2022-07-12 14:14:15
目前,我正在比较几种传统的方法,在一系列点中选择指数趋势。在我的行业中,趋势的选择往往不考虑适合度的度量,这意味着一种常见的方法是简单地测量yr/yr的变化,并在一段时间内对这些结果进行平均值。这会产生一个因素,但不会产生拟合,因此很难将其与指数回归或其他方法相比较。所以我的问题是:
如果我对指数曲线有一个预先选择的、固定的趋势因子,那么是否有一种简单的方法来优化“截距”值,以最小化对一组数据的总体拟合的平方误差?请考虑以下几点:
import numpy as np
from sklearn.metrics import r2_score
from scipy.optimize import curve_fit
#Define exponential function
def ex(x,a,b):
return a*b**x
#Seed data with normally distributed error
x=np.linspace(1,20,20)
np.random.seed(100)
y=ex(x,100,1.01)+3*np.random.randn(20)
#Exponential regression for trend value, fitted values, and r_sq measure
popt, pcov = curve_fit(ex, x, y)
trend,fit,r_sq=(popt[1])-1, ex(x,*popt), r2_score(y,ex(x,*popt))
#Mean Yr/Yr change as an alternative measure of trend
trend_yryr=np.mean(np.diff(y)/y[1:])
print(trend)
print(trend_yryr)年/年的平均变化为数据产生了不同的趋势值,我想将其与指数回归的选定趋势进行比较。我的目标是找到截距,这将最小化这个替代趋势值对数据的平方误差,并测量该平方误差进行比较。谢谢你的帮助。
回答 1
Stack Overflow用户
回答已采纳
发布于 2022-07-12 23:35:40
使用curve_fit时修复参数的一种方法是传递一个lambda函数,该函数对要修复的参数进行硬编码。我就是这样做的:
# ... all your preamble, but importing matplotlib
new_b = trend_yryr + 1
popt2, pcov2 = curve_fit(lambda x, a: ex(x, a, new_b), x, y)
fit2, r_sq2 = ex(x, *popt2, new_b), r2_score(y, ex(x, *popt2, new_b))popt是array([100.24989416, 1.00975864]),popt2是array([99.09513612])。绘制结果给我的结果是:
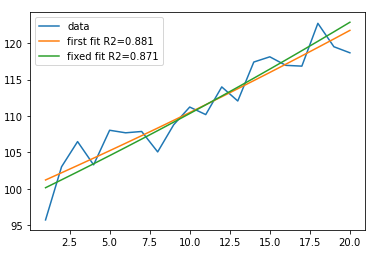
您可以使用lmfit进行更优雅的操作,但本质上取决于您。
from lmfit import Parameters, minimize
def residual(params, x, y):
a = params['a']
b = params['b']
model = ex(x, a, b)
return model - y
p1 = Parameters()
p1.add('a', value=1, vary=True)
p1.add('b', value=1, vary=True)
p2 = Parameters()
p2.add('a', value=1, vary=True)
p2.add('b', value=np.mean(np.diff(y)/y[1:]) + 1, vary=False) # important
out1 = minimize(residual, p1, args=(x, y))
out2 = minimize(residual, p2, args=(x, y))这两种方法的输出本质上是相同的,所以我不会再发布它们
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/72953792
复制相关文章
相似问题

