朱莉娅如何做预谋
朱莉娅如何做预谋
提问于 2022-07-19 07:46:37
我有这个R码,用来模拟正态分布的对数返回。我已经理解了代码,但缺乏一些知识来将其完全转换为Julia。
R-代码
rt.sim<-rnorm(sim.size,mean=(mu_hat-s^2/2),sd=s)
Asset.sim<-rep(NA,sim.size)
Asset.sim[1]<-Asset[n]*exp(rt.sim[1])
for(i in 2:sim.size)Asset.sim[i]<-Asset.sim[i-1]*exp(rt.sim[i])
yl<-min(Asset)*0.85
yu<-max(Asset)*1.9
plot(ts(Asset),xlim=c(0,(n+sim.size)),ylim=c(yl,yu))
lines((n+1):(n+sim.size),Asset.sim,col="red",lwd=2)
grid(col="black",lwd=2)这是我的朱莉娅版本。我用这种方式尝试,得到了这个代码的错误。有人能帮我把它修好吗?Julia Code
FTSE = df[!,"FTSE"]
Asset = FTSE
sim.size = 500 #got error here
n = length(Asset)
## log-return
rt = diff(log.(Asset))
rbar = mean(rt)
s = sd(rt)
delta_t = 1
mu_hat = rbar+s^2/2
Random.seed!(123)
## Simulate log-return from Normal distribution
rt.sim = rand(Normal(s^2/2, s),sim.size)
Asset.sim = Vector{Int}(undef,sim.size)
Asset.sim[1] = Asset[n]*exp(rt.sim[1])
for i in 2:sim.size
Asset.sim[i] = Asset.sim[i-1]*exp(rt.sim[i])
end
yl = min(Asset)*0.85
yu = max(Asset)*1.9
plot(ts(Asset),xlim=c(0,(n+sim.size)),ylim=c(yl,yu))
lines((n+1):(n+sim.size),Asset.sim,col="red",lwd=2)
# grid(col="black",lwd=2)回答 1
Stack Overflow用户
回答已采纳
发布于 2022-07-19 09:10:52
正如Bogumil所言,您需要从在变量名中使用.转移到_或其他一些替代方法。
您的问题中的绘图命令根本不是Julia语法,下面是一个完整的可重复的示例:
using DataFrames, Distributions, MarketData, Plots, Statistics
# Get data from Yahoo
df = dropmissing(select(DataFrame(yahoo("^FTSE")), :timestamp, :AdjClose));
# Restricting range to have a similar number of observations to your plot
ftse = df.AdjClose[end-1900:end];
# Simulation dimensions
sim_size = 500;
n = length(ftse);
# Simulate log returns
log_return = diff(log.(ftse));
r̄ = mean(log_return);
σ = std(log_return);
μ̂ = r̄ + σ^2/2;
rt_sim = rand(Normal(σ^2/2, σ), sim_size);
# More concise way of writing the loop
asset_sim = ftse[end] .* exp.(cumsum(rt_sim));
# Plot observed data and add simulated data to plot
plot(ftse, color = "black", xlabel = "Time", ylabel = "Close", label = "Observed data", legend = :topleft)
plot!(n+1:n+sim_size, asset_sim, color = "red", label = "Simulated data")这意味着:
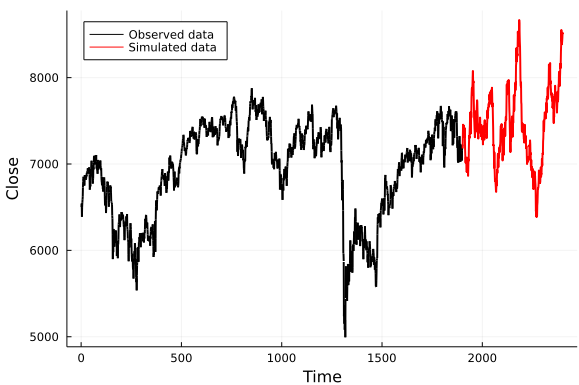
(很明显,我一直在使用与你不同的日期范围。另外,您的模拟似乎有更强的正向趋势,请注意,在R中,您使用的是看起来像波动率调整后的平均回报,在Julia版本中,您创建了一个μ̂变量,但实际上是使用σ^2/2作为绘制模拟回报的平均回报)。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/73033025
复制相关文章
相似问题

