使用scipy.stats.linregress的标准误差生成线性拟合样本
我使用scipy.stats.linregress来拟合一组点,如下图所示。点是蓝色圆,线性拟合是黑线,灰色线是使用stderr和intercept_stderr值采集的样本,用numpy.random.normal (下面的代码)对slope和intercept值进行采样。
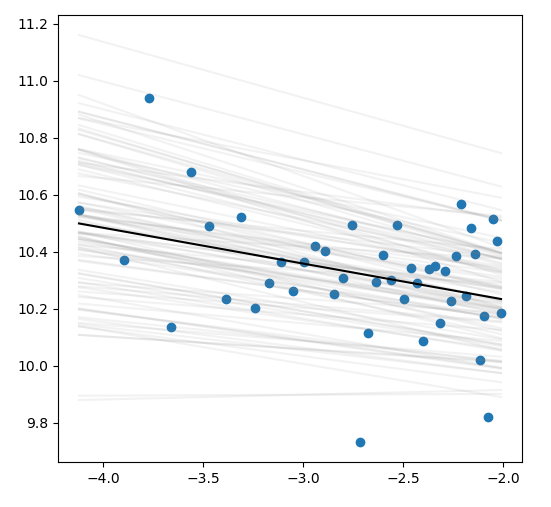
我的问题是:假设stderr和intercept_stderr是标准误差,numpy.random.normal期望标准差,那么当采样时,是否应该将stderr和intercept_stderr乘以$\sqrt{N}$?
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
x = np.array([-4.12078708, -3.89764352, -3.77248038, -3.66125475, -3.56117129,
-3.47019951, -3.3868179 , -3.30985686, -3.2383979 , -3.17170652,
-3.10918616, -3.05034566, -2.99477581, -2.94213208, -2.89212166,
-2.84449361, -2.79903124, -2.75554612, -2.71387343, -2.67386809,
-2.63540181, -2.59836054, -2.56264246, -2.52815628, -2.49481986,
-2.462559 , -2.43130646, -2.40100111, -2.37158722, -2.34301385,
-2.31523428, -2.28820561, -2.2618883 , -2.23624587, -2.21124457,
-2.18685312, -2.16304247, -2.13978561, -2.11705736, -2.09483422,
-2.07309423, -2.05181683, -2.03098275, -2.01057388])
y = np.array([10.54683181, 10.37020828, 10.93819231, 10.1338195 , 10.68036321,
10.48930797, 10.2340761 , 10.52002056, 10.20343913, 10.29089844,
10.36190947, 10.26050936, 10.36528216, 10.41799894, 10.40077834,
10.2513676 , 10.30768792, 10.49377725, 9.73298189, 10.1158334 ,
10.29359023, 10.38660209, 10.30087358, 10.49464606, 10.23305099,
10.34389097, 10.29016557, 10.0865885 , 10.338077 , 10.34950896,
10.15110388, 10.33316701, 10.22837808, 10.3848174 , 10.56872297,
10.24457621, 10.48255182, 10.39029786, 10.0208671 , 10.17400544,
9.82086658, 10.51361151, 10.4376062 , 10.18610696])
res = stats.linregress(x, y)
s_vals = np.random.normal(res.slope, res.stderr, 100)
i_vals = np.random.normal(res.intercept, res.intercept_stderr, 100)
for i in range(100):
plt.plot(x, i_vals[i] + s_vals[i]*x, c='grey', alpha=.1)
plt.scatter(x, y)
plt.plot(x, res.intercept + res.slope*x, c='k')
plt.show()回答 1
Stack Overflow用户
发布于 2022-08-13 00:07:27
TL;DR
实际上,它是对标准偏差的估计,因为标准误差是特定参数的误差的标准差。不,没有必要通过与np.sqrt(n)相乘来“去正常化”。但是,最后,您可能希望更改模拟参数与t-distribution的分布。
定性解释
不需要进一步的乘法(例如与np.sqrt(n)),即规范化保持在适当的位置。为什么会这样呢?从直觉上说,斜率和截距参数从某种意义上说是由x对和y对组成的数据集的汇总统计,它们把数据集描述为一个整体,而不是一个单一的点(x_i,y_i)。类似于抽样汇总统计量(例如,平均值x),我们使用标准化估计量来计算标准差。在回归的情况下,数据集中所有数据点的平均可变性会影响结果拦截的估计变异性。样本大小的平方根仅平衡数据点之间相对于绝对值的可变性之和。
更严格的解释将涉及估计量的方差协方差矩阵(β^)。其中,元素沿对角线方向的平方根是估计量元素的标准误差。特别是对角线上第一个元素的平方根,它表示截距参数的标准误差。用一点线性代数,我们可以在每个参数的标准误差(在你的例子中,截距和斜率)和回归模型的标准误差之间建立一个联系。由于回归模型s的标准误差是对数据σ中噪声标准差的渐近无偏估计,因此可以建立一个不需要对截距标准差进行再缩放的定量理论基础。
关于您采样/模拟拦截和斜率的分布。标准错误不是正态分布,而是服从(学生的)t分布.见幻灯片18。反过来,
s_vals = np.random.standard_t(df=len(x)-2, size=100) * res.stderr + res.slope
i_vals = np.random.standard_t(df=len(x)-2, size=100) * res.intercept_stderr + res.intercept然而,由于样本大小超出了n=30,与从高斯分布中取样的结果相比,实现几乎在统计上是无法区分的。这是因为t分布较快地收敛于标准正态分布.
视觉解释
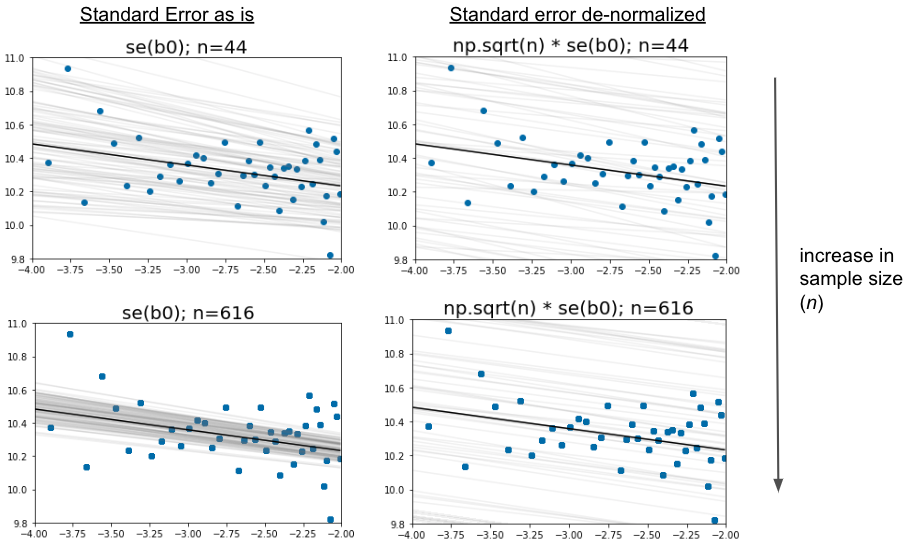
不过,我们可以跳过定量论点。我们对基于数据集的估计器有什么期望?我们拥有的数据越多,我们对固定但未知位置的确定性就越强。反过来,如果我们增加数据的大小n,模拟的灰色线应该更靠近一起。当我们使用标准错误作为scale参数时,就会发生这种情况。将样本数量增加14倍,就会使灰色线更加接近。相反,即使数据集的大小急剧增加,使用标准误差乘以np.sqrt(n)也会使灰线相隔很远。事实上,我们正是通过与n的平方根相乘来消除高样本数的优点。
https://stackoverflow.com/questions/73339791
复制相似问题

