递归(某种子集和,但不完全是)-如果真能以确切的价格购买钢笔,否则是假的。
我有一个问题:你有一张7,9,11支钢笔的清单。你有一个功能:
def can_i_buy(x):你需要检查一下你是否能买到确切的数量。
例如,我有X=23
我可以买1*9, 2*7
我只需要返回真,如果它是可以的,假的其他。
我看到了答案,他们用3的蛮力做循环(疯狂)。
我试过递归,它很好,但似乎是长+重复的部分+它不是很好,因为我不知道把假陈述放在哪里。我的出口点是什么。
代码有效,但不完全正确。
def can_i_buy(x): # 23
return helper(x, [7,9,11])
def helper(x, lst):
if x == 0:
return True
if x < 0:
return
take_1 = helper(x - lst[0], lst)
if take_1 == True:
return take_1
take_2 = helper(x - lst[1], lst)
if take_2 == True:
return take_2
take_3 = helper(x - lst[2], lst)
if take_3 == True:
return take_3怎么修呢?另外,我在这里的出口声明是什么想法?我不知道怎么退出..。我该把假写在哪里,怎么写?
编辑:添加印刷品+输出
print(can_i_buy(24))
print(can_i_buy(23))
print(can_i_buy(7))
print(can_i_buy(14))产出:
None
True
True
True我不应该收到-假的。但我不知道该把虚假陈述放哪儿..。当所有递归结束时,我不知道该怎么说。
回答 5
Stack Overflow用户
发布于 2022-08-30 08:31:54
递归调用应从x中减去每个价格,直到x为0(在这种情况下为返回True)或小于0(在这种情况下为返回False):
def can_i_buy(x, lst):
return not x or x > 0 and any(can_i_buy(x - i, lst) for i in lst)如果只想修复代码,则可以在函数结束时返回False,当返回True的所有条件都通过时:
def helper(x, lst):
if x == 0:
return True
if x > 0:
take_1 = helper(x - lst[0], lst)
if take_1 == True:
return take_1
take_2 = helper(x - lst[1], lst)
if take_2 == True:
return take_2
take_3 = helper(x - lst[2], lst)
if take_3 == True:
return take_3
return False或者如果允许您做一个for循环:
def helper(x, lst):
if x == 0:
return True
if x > 0:
for i in lst:
if helper(x - i, lst):
return True
return FalseStack Overflow用户
发布于 2022-08-30 08:33:56
这个问题是一个无界背包的特殊情况,允许重复的项目。这类似于硬币换币(或做出改变)问题,但你只需要找出它是否有可能,而不是找到最小数量的硬币,而不是一定数量的硬币。这类问题具有动态规划性质,通常通过递归求解.
直觉:
基本上,当你第一次遇到这样的问题时,蛮力是正确的选择。例如,我们有一个值[11, 9, 7]的列表,我们想知道是否可以使用这些硬币的总和来得到23。我们可以探索每一个可能的组合来验证这一点。
蛮力
想出蛮力解决方案相对容易,这里的递归非常简单:
def can_i_buy(alist, target):
if target == 0:
return True
if target < 0:
return False
for i in range(len(alist)):
if can_i_buy(alist, target - alist[i]):
return True
return False我画了一个函数调用图来显示这里发生的事情(我没有在这里放置所有的分支来使它更加紧凑):
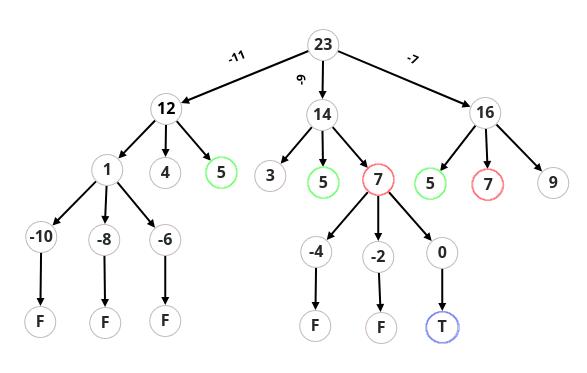
我敢打赌你在这里很容易找到不需要的工作,对吧?看看绿点和红点,如果我们已经用值5计算了节点的结果(对于7也是一样),那么我们真的需要稍后再计算它吗?我们能以某种方式缓存以前计算出来的结果吗?是的,我们可以通过回忆录(您也可以使用@cache装饰器而不是显式缓存)。
自上而下的回忆录
memo = {}
def can_i_buy(alist, target):
if target == 0:
return True
if target < 0:
return False
if target in memo:
return memo[target]
for i in range(len(alist)):
diff = target - alist[i]
memo[diff] = can_i_buy(alist, diff)
if memo[diff]:
return True
return False
print(can_i_buy([11, 9, 7], 23))
print(memo) # {-10: False, -8: False, -6: False, 1: False, -4: False, 3: False, -2: False, 5: False, 12: False, 0: True, 7: True, 14: True}还有一种方法叫做自下而上。通常,这是很难想出,但它更好地显示了子问题之间的关系。
自下而上
def can_i_buy(target):
dp = [True] + [False] * target
for num in range(1, target + 1):
for coin in alist:
if num - coin >= 0:
dp[num] = dp[num] or dp[num - coin]
return dp[target]您也可以使用广度优先搜索方法,它非常类似于自上而下的方法.
宽度第一
from collections import deque
def can_i_buy(alist, target):
seen = set()
queue = deque([target])
while queue:
t = queue.popleft()
if t == 0:
return True
for val in alist:
diff = t - val
if diff >= 0 and diff not in seen:
queue.append(t - val)
seen.add(diff)
return FalseStack Overflow用户
发布于 2022-08-30 09:04:30
我采用了宽度优先搜索和动态规划相结合的技术来解决这类问题。您可以根据用例来更改它(例如,如果我们需要返回如何创建值的话)。
def can_i_buy(target_value, values):
possible_values = {0: True}
values_to_be_handled = [0]
while values_to_be_handled:
value = values_to_be_handled.pop(0)
if value == target_value:
return True
for val in values:
next_value = value + val
if next_value > target_value:
continue
if next_value not in possible_values:
possible_values[next_value] = True
values_to_be_handled.append(next_value)
return Nonehttps://stackoverflow.com/questions/73539270
复制相似问题

